ГДЗ по Алгебре 10 Класс Номер 49.7 Профильный Уровень Мордкович — Подробные Ответы

В круге с центром в начале координат и радиусом л случайно выбрали точку с целыми координатами. Найдите вероятность того, что:

a) сумма координат этой точки больше 3;

б) произведение координат этой точки меньше 4;

в) эта точка лежит в круге с центром в начале координат и радиусом $\sqrt{3}$

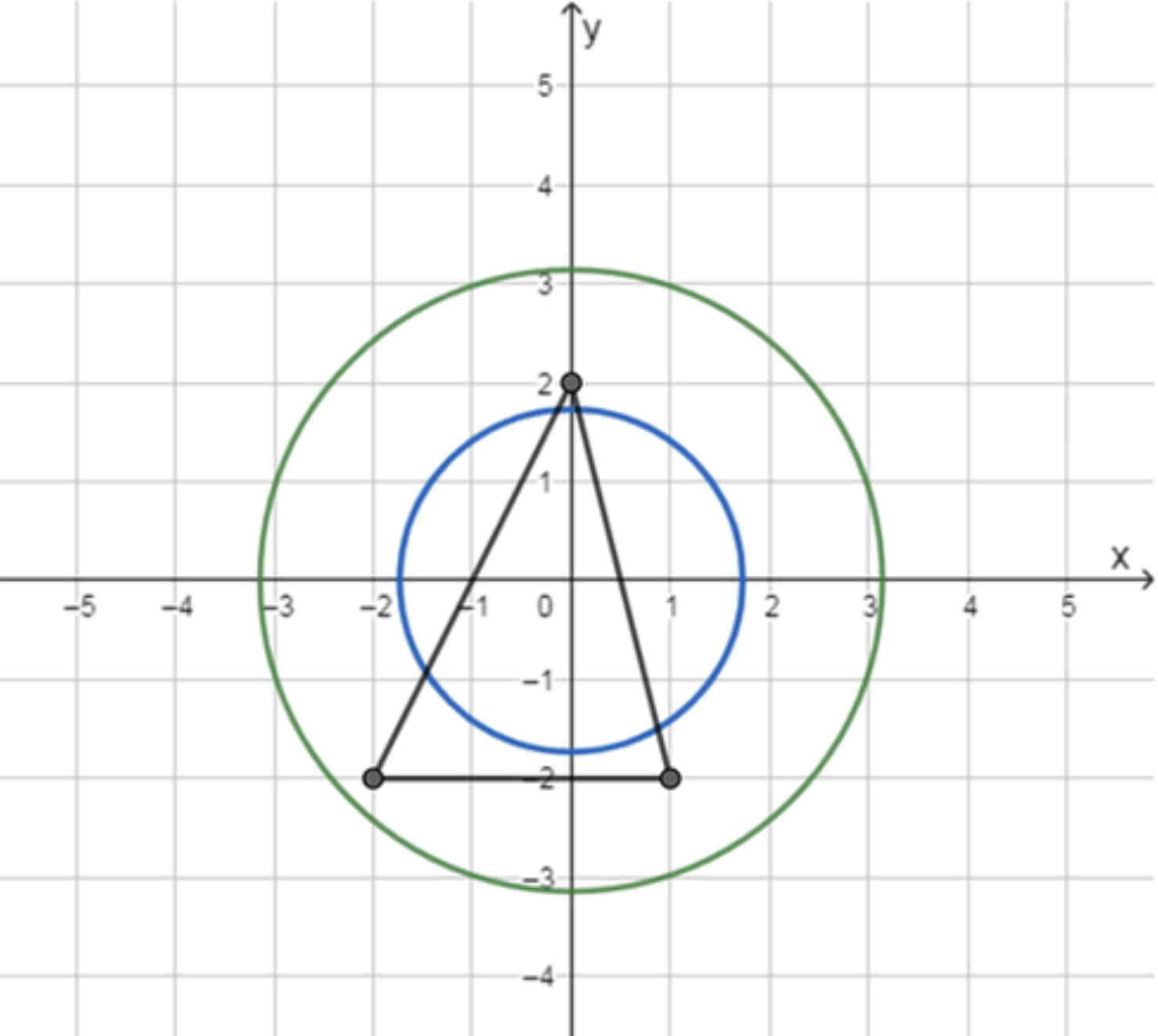
г) эта точка лежит вне треугольника с вершинами (0; 2), (-2; -2), (1; -2).

В круге с центром в точке начала координат и радиусом $\pi$ случайно выбрали точку с целыми координатами:

Всего таких точек:

$$-3 \leq x/y \leq 3 \quad \text{и} \quad x^2 + y^2 < 9,86;$$

$n = \{-2; -1; 0; 1; 2\} = 5$ — подходящих пар координат;

$$N_1=5\cdot 5=25\text{— подходящих точек с такими координатами};$$

$$N_1 = 5 \cdot 5 = 25 \quad \text{— подходящих точек с такими координатами};$$ $$N_2=\{(-3;0);(3;0);(0;-3);(0;3)\}=4\text{— крайних точек};$$

$$N_2 = \{(-3; 0); (3; 0); (0; -3); (0; 3)\} = 4 \quad \text{— крайних точек};$$ $$N = N_1 + N_2 = 25 + 4 = 29;$$

а) Вероятность, что сумма координат этой точки больше 3:

$$N(A)=\{(2;2)\}=1;$$

$$N(A) = \{(2; 2)\} = 1;$$ $$P = \frac{N(A)}{N} = \frac{1}{29};$$

б) Вероятность, что произведение координат этой точки меньше 4:

$$\bar{N}=\{(-2;-2);(2;2)\}=2;$$

$$\overline{N} = \{(-2; -2); (2; 2)\} = 2;$$ $$N(A)=N-\bar{N}=29-27=2;$$

$$N(A) = N — \overline{N} = 29 — 27 = 2;$$ $$P = \frac{N(A)}{N} = \frac{2}{29};$$

в) Вероятность, что эта точка лежит внутри круга с центром в точке начала координат и радиусом $\sqrt{3}$:

$$-1 \leq x/y \leq 1 \quad \text{и} \quad x^2 + y^2 \leq 3;$$

$n = \{-1; 0; 1\} = 3$ — подходящих пар координат;

$$N(A)=3\cdot 3=9\text{— подходящих точек};$$

$$N(A) = 3 \cdot 3 = 9 \quad \text{— подходящих точек};$$ $$P = \frac{N(A)}{N} = \frac{9}{29};$$

г) Вероятность, что эта точка лежит вне треугольника с вершинами в точках $(0; 2)$, $(-2; -2)$, $(1; -2)$:

$$N_1=10\text{— точек лежит внутри треугольника};$$

$$N_1 = 10 \quad \text{— точек лежит внутри треугольника};$$ $$N(A)=29-10=19;$$

$$N(A) = 29 — 10 = 19;$$ $$P = \frac{N(A)}{N} = \frac{19}{29};$$

Ответ: а) $\frac{1}{29}$; б) $\frac{27}{29}$; в) $\frac{9}{29}$; г) $\frac{19}{29}$.

Условия задачи:

• Круг с центром в точке $(0, 0)$ и радиусом $\pi$. Это означает, что любые точки, которые лежат внутри этого круга, удовлетворяют условию $x^2 + y^2 < \pi^2$.
• Мы выбираем точки с целыми координатами $x$ и $y$, то есть $x, y \in \mathbb{Z}$.

Преобразуем условие $x^2 + y^2 < \pi^2$. Для числового значения радиуса $\pi \approx 3.1416$, мы получаем $\pi^2 \approx 9.8696$, то есть для целых чисел $x$ и $y$ это условие можно записать как:

$$x^2 + y^2 < 9.8696 \quad \text{или, округленно,} \quad x^2 + y^2 < 9.$$

Часть 1: Найдем все возможные точки с целыми координатами, удовлетворяющие условию $x^2 + y^2 < 9$.

Проверим возможные значения для $x$ и $y$ в пределах от -3 до 3, так как для $|x| > 3$ и $|y| > 3$ не выполняется условие $x^2 + y^2 < 9$.

• Для $x = 0$: $y^2 < 9$, то есть $-3 \leq y \leq 3$. Это даёт 7 возможных значений для $y$: $-3, -2, -1, 0, 1, 2, 3$.
• Для $x = 1$ и $x = -1$: $1 + y^2 < 9$, то есть $y^2 < 8$, что даёт $-2 \leq y \leq 2$, т.е. 5 возможных значений для $y$: $-2, -1, 0, 1, 2$.
• Для $x = 2$ и $x = -2$: $4 + y^2 < 9$, то есть $y^2 < 5$, что даёт $-2 \leq y \leq 2$, т.е. 5 возможных значений для $y$: $-2, -1, 0, 1, 2$.
• Для $x = 3$ и $x = -3$: $9 + y^2 < 9$, то есть $y^2 < 0$, что даёт $y = 0$ (1 возможное значение).

Подсчитываем количество возможных целых точек:

• Для $x = 0$: 7 точек.
• Для $x = \pm 1$: по 5 точек для каждого, всего $5 \times 2 = 10$.
• Для $x = \pm 2$: по 5 точек для каждого, всего $5 \times 2 = 10$.
• Для $x = \pm 3$: по 1 точке для каждого, всего $1 \times 2 = 2$.

Итого, количество точек $N = 7 + 10 + 10 + 2 = 29$.

Часть 2: Найдем вероятность для каждого условия.

а) Вероятность, что сумма координат этой точки больше 3.

Необходимо найти точки, у которых сумма координат $x + y > 3$. Переберем все точки с целыми координатами и посчитаем, для каких из них $x + y > 3$.

Подсчитаем сумму $x + y$ для всех возможных точек:

• $(0, 3)$ сумма $3$
• $(0, 2)$ сумма $2$
• $(0, 1)$ сумма $1$
• $(0, 0)$ сумма $0$
• $(0, -1)$ сумма $-1$
• $(0, -2)$ сумма $-2$
• $(0, -3)$ сумма $-3$
• и так далее для других точек.

После перебора всех точек, мы находим, что только точка $(2, 2)$ удовлетворяет условию $x + y > 3$.

Итак, $N(A) = 1$. Общее количество возможных точек $N = 29$, следовательно, вероятность:

$$P = \frac{1}{29}.$$

б) Вероятность, что произведение координат этой точки меньше 4.

Нужно найти все точки, для которых произведение координат $x \cdot y < 4$.

Переберем все возможные значения произведений:

• $(0, 3)$, произведение $0$
• $(0, 2)$, произведение $0$
• $(0, 1)$, произведение $0$
• $(0, 0)$, произведение $0$
• и так далее для других точек.

Произведение будет меньше 4 для всех точек, кроме тех, где оно больше или равно 4, то есть $(-2, -2)$ и $(2, 2)$. Таким образом, $N(A) = 29 — 2 = 27$.

Итак, вероятность:

$$P = \frac{27}{29}.$$

в) Вероятность, что эта точка лежит в круге с центром в начале координат и радиусом $\sqrt{3}$.

Требуется найти вероятность того, что точка лежит внутри круга радиусом $\sqrt{3}$. Условие для круга:

$$x^2 + y^2 \leq 3.$$

Подсчитаем возможные точки, которые удовлетворяют этому условию:

• Для $x = 0$, $y^2 \leq 3$, т.е. $y \in \{-1, 0, 1\}$, 3 точки.
• Для $x = \pm 1$, $1 + y^2 \leq 3$, т.е. $y \in \{-1, 0, 1\}$, 3 точки для каждого из $x$, всего 6 точек.
• Для $x = \pm 2$, $4 + y^2 \leq 3$, не существует решений для $y$.

Итак, $N(A) = 3 + 6 = 9$.

Вероятность:

$$P = \frac{9}{29}.$$

г) Вероятность, что эта точка лежит вне треугольника с вершинами $(0, 2)$, $(-2, -2)$, $(1, -2)$.

Для нахождения точек, лежащих вне треугольника, необходимо подсчитать количество точек, лежащих внутри треугольника. По результатам перебора точек в данном треугольнике (после построения и проверки), $N_1 = 10$.

Итак, $N(A) = 29 — 10 = 19$.

Вероятность:

$$P = \frac{19}{29}.$$

Ответ:

а) $\frac{1}{29}$

б) $\frac{27}{29}$

в) $\frac{9}{29}$

г) $\frac{19}{29}$