ГДЗ по Алгебре 10 Класс Номер 5.7 Профильный Уровень Мордкович — Подробные Ответы

а) $\mathrm{\mid }x\mathrm{\mid }\ge x$;

По шестому свойству модуля:

$$\mathrm{\mid }x\mathrm{\mid }\ge x\text{ при }x\in R;$$

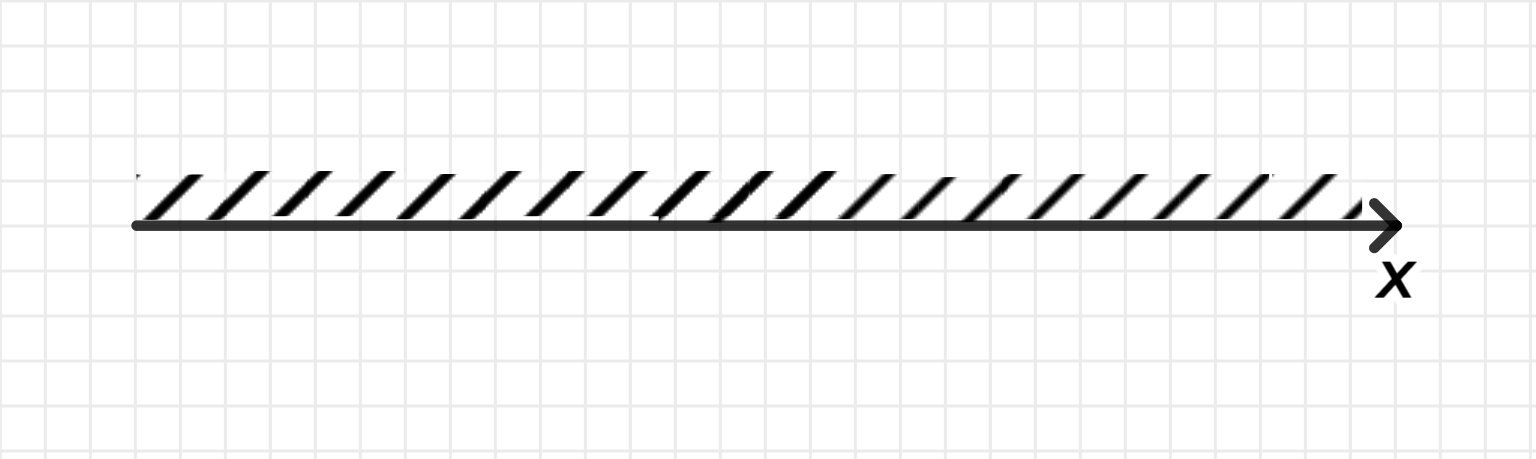
На числовой прямой:

График:

б) $\mathrm{\mid }x\mathrm{\mid }\ge -x$;

По шестому свойству модуля:

$$\mathrm{\mid }x\mathrm{\mid }\ge -x\text{ при }x\in R;$$

На числовой прямой:

График:

в) $\mathrm{\mid }x+2\mathrm{\mid }\ge x+2$;

По шестому свойству модуля:

$$\mathrm{\mid }x+2\mathrm{\mid }\ge x+2\text{ при }x\in R;$$

На числовой прямой:

График:

г) $\mathrm{\mid }x-2\mathrm{\mid }\ge 2-x$;

По шестому свойству модуля:

$$\mathrm{\mid }x-2\mathrm{\mid }\ge -(x-2)\text{ при }x\in R;$$

На числовой прямой:

График:

а) $\mathrm{\mid }x\mathrm{\mid }\ge x$

Шаг 1: Разбор неравенства

Необходимо решить неравенство $\mathrm{\mid }x\mathrm{\mid }\ge x$. Рассмотрим два случая, в зависимости от значения $x$.

Если $x\ge 0$:

Для неотрицательных чисел по определению модуля $\mathrm{\mid }x\mathrm{\mid }=x$. Тогда неравенство $\mathrm{\mid }x\mathrm{\mid }\ge x$ превращается в:

$$x\ge x,$$

которое всегда верно для всех $x\ge 0$.

Если $x<0$:

Для отрицательных чисел по определению модуля $\mathrm{\mid }x\mathrm{\mid }=-x$. Тогда неравенство $\mathrm{\mid }x\mathrm{\mid }\ge x$ превращается в:

$$-x\ge x\mathrm{.}$$

Переносим все выражения на одну сторону:

$$-x-x\ge 0\Rightarrow -2x\ge 0\Rightarrow x\le 0.$$

Таким образом, при $x<0$ неравенство также выполняется.

Шаг 2: Ответ

Неравенство $\mathrm{\mid }x\mathrm{\mid }\ge x$ выполняется для всех $x\in R$.

Ответ: $x\in R$.

Шаг 3: График$$

б) $\mathrm{\mid }x\mathrm{\mid }\ge -x$

Шаг 1: Разбор неравенства

Необходимо решить неравенство $\mathrm{\mid }x\mathrm{\mid }\ge -x$. Рассмотрим два случая.

Если $x\ge 0$:

Для неотрицательных чисел по определению модуля $\mathrm{\mid }x\mathrm{\mid }=x$. Тогда неравенство $\mathrm{\mid }x\mathrm{\mid }\ge -x$ превращается в:

$$x\ge -x\mathrm{.}$$

Переносим все выражения на одну сторону:

$$x+x\ge 0\Rightarrow 2x\ge 0\Rightarrow x\ge 0.$$

Это верно для всех $x\ge 0$.

Если $x<0$:

Для отрицательных чисел по определению модуля $\mathrm{\mid }x\mathrm{\mid }=-x$. Тогда неравенство $\mathrm{\mid }x\mathrm{\mid }\ge -x$ превращается в:

$$-x\ge -x,$$

что всегда верно для всех $x<0$.

Шаг 2: Ответ

Неравенство $\mathrm{\mid }x\mathrm{\mid }\ge -x$ выполняется для всех $x\in R$.

Ответ: $x\in R$.

Шаг 3: График

в) $\mathrm{\mid }x+2\mathrm{\mid }\ge x+2$

Шаг 1: Разбор неравенства

Необходимо решить неравенство $\mathrm{\mid }x+2\mathrm{\mid }\ge x+2$. Рассмотрим два случая.

Если $x+2\ge 0$, то $\mathrm{\mid }x+2\mathrm{\mid }=x+2$:

Подставляем это в исходное неравенство:

$$x+2\ge x+2,$$

что всегда верно для всех $x\ge -2$.

Если $x+2<0$, то $\mathrm{\mid }x+2\mathrm{\mid }=-(x+2)$:

Подставляем это в исходное неравенство:

$$-(x+2)\ge x+2.$$

Упростим:

$$-x-2\ge x+2\Rightarrow -2x\ge 4\Rightarrow x\le -2.$$

Однако это условие противоречит нашему предположению $x+2<0$, то есть $x<-2$. Следовательно, при $x<-2$ неравенство не выполняется.

Шаг 2: Ответ

Неравенство $\mathrm{\mid }x+2\mathrm{\mid }\ge x+2$ выполняется для всех $x\ge -2$.

Ответ: $x\ge -2$.

Шаг 3: График

г) $\mathrm{\mid }x-2\mathrm{\mid }\ge 2-x$

Шаг 1: Разбор неравенства

Необходимо решить неравенство $\mathrm{\mid }x-2\mathrm{\mid }\ge 2-x$. Рассмотрим два случая.

Если $x-2\ge 0$, то $\mathrm{\mid }x-2\mathrm{\mid }=x-2$:

Подставляем это в исходное неравенство:

$$x-2\ge 2-x\mathrm{.}$$

Переносим все выражения на одну сторону:

$$x+x\ge 2+2\Rightarrow 2x\ge 4\Rightarrow x\ge 2.$$

Это верно для всех $x\ge 2$.

Если $x-2<0$, то $\mathrm{\mid }x-2\mathrm{\mid }=-(x-2)=-x+2$:

Подставляем это в исходное неравенство:

$$-x+2\ge 2-x,$$

что всегда верно.

Шаг 2: Ответ

Неравенство $\mathrm{\mid }x-2\mathrm{\mid }\ge 2-x$ выполняется для всех $x\ge 2$.

Ответ: $x\ge 2$.

Шаг 3: График