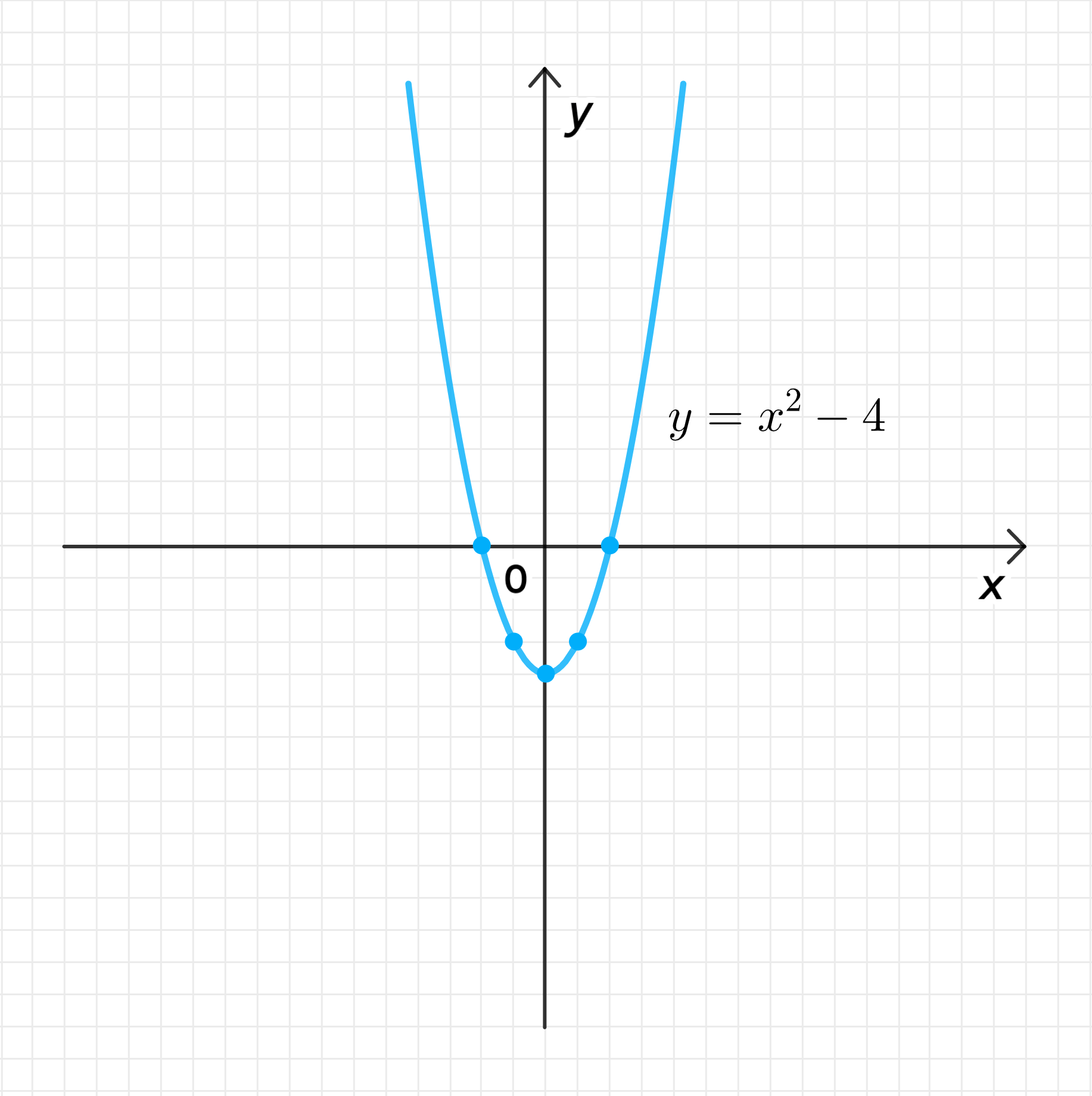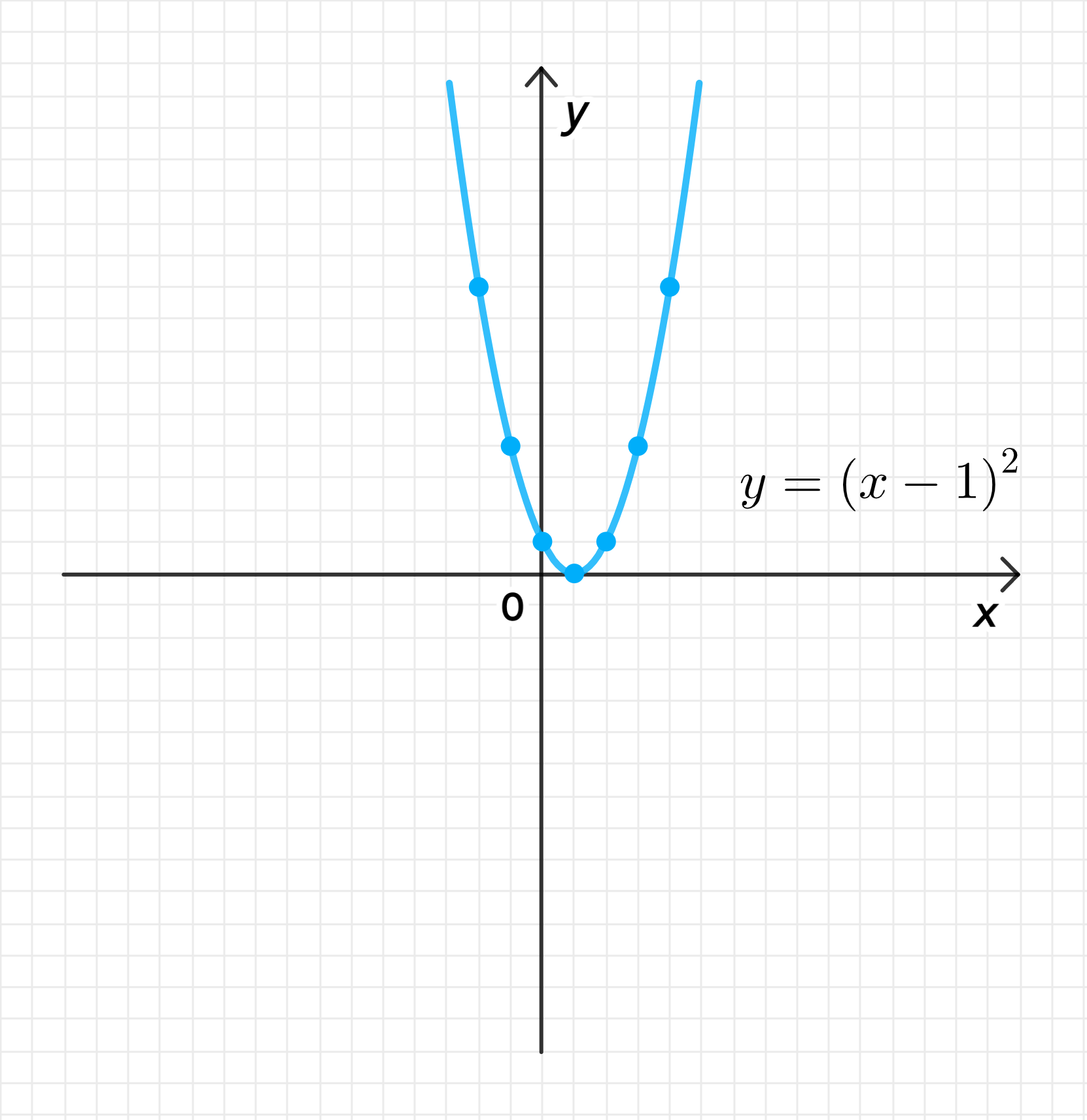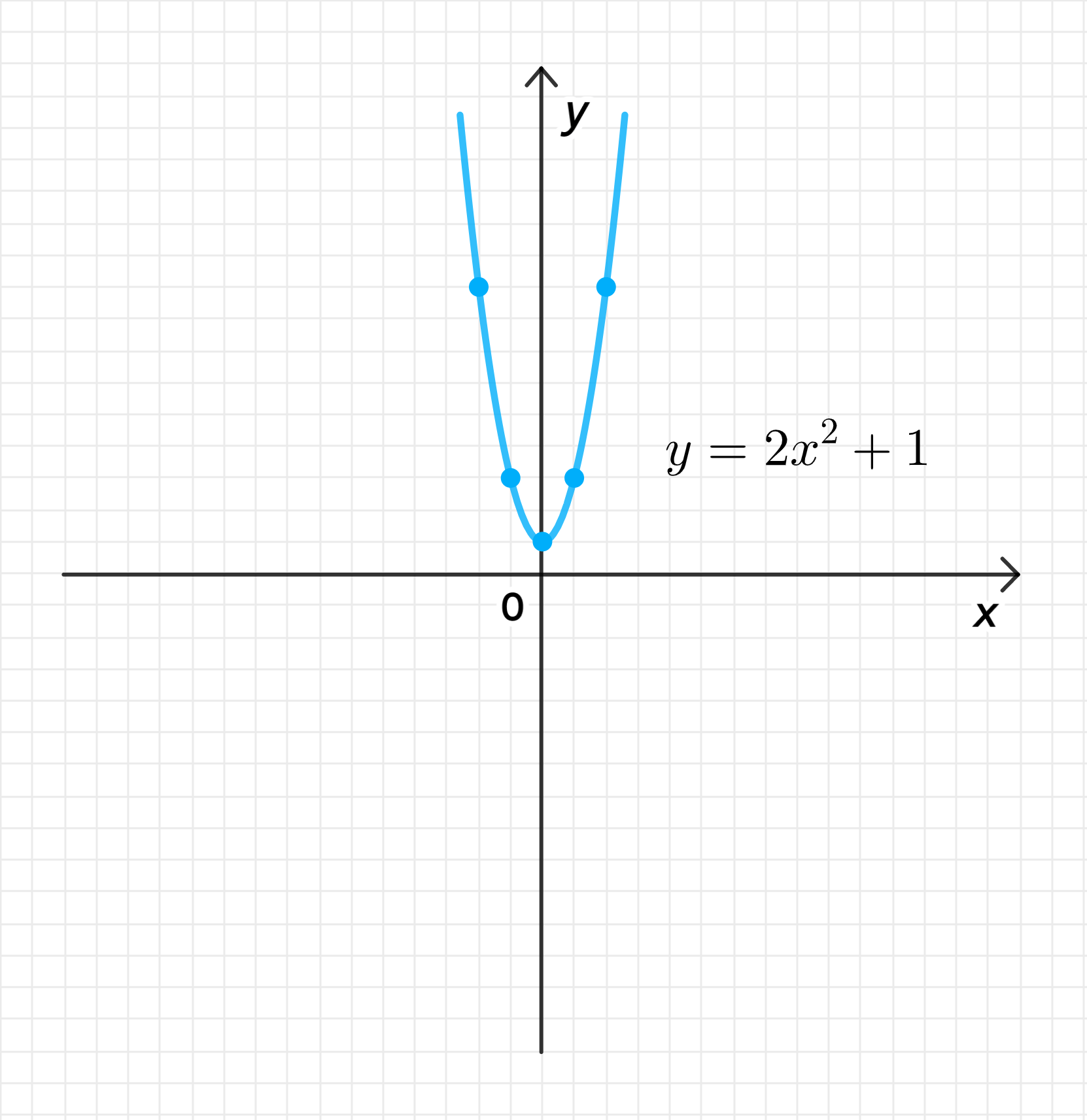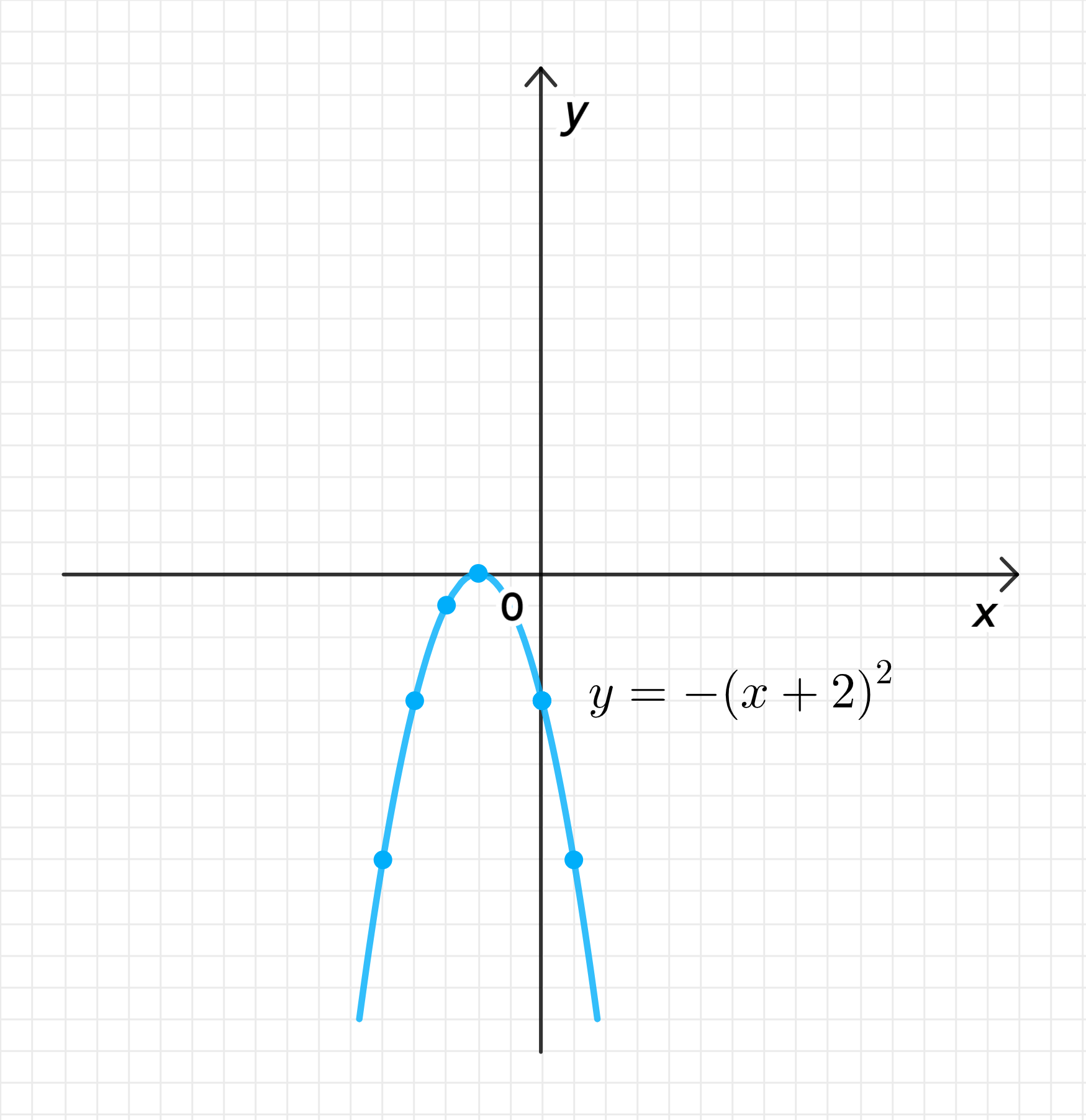ГДЗ по Алгебре 10 Класс Номер 7.14 Профильный Уровень Мордкович — Подробные Ответы

а) $y = x^2 — 4$;

б) $y = (x — 1)^2$;

в) $y = 2x^2 + 1$;

г) $y = -(x + 2)^2$

а) $y = x^2 — 4$;

• Область определения: $x \in \mathbb{R}$;
• Множество значений: $y \geq -4$;
• Координаты вершины параболы:

  $$x_0 = 0 \quad \text{и} \quad y_0 = -4;$$

• Координаты некоторых точек:

  $$\begin{array}{|c|c|c|c|c|c|c|} \hline x & -3 & -2 & -1 & 1 & 2 & 3 \\ \hline y & 5 & 0 & -3 & -3 & 0 & 5 \\ \hline \end{array}$$

• График функции:

б) $y = (x — 1)^2$;

• Область определения: $x \in \mathbb{R}$;
• Множество значений: $y \geq 0$;
• Координаты вершины параболы:

  $$x_0 = 1 \quad \text{и} \quad y_0 = 0;$$

• Координаты некоторых точек:

  $$\begin{array}{|c|c|c|c|c|c|c|} \hline x & -2 & -1 & 0 & 2 & 3 & 4 \\ \hline y & 9 & 4 & 1 & 1 & 4 & 9 \\ \hline \end{array}$$

• График функции:

в) $y = 2x^2 + 1$;

• Область определения: $x \in \mathbb{R}$;
• Множество значений: $y \geq 1$;
• Координаты вершины параболы:

  $$x_0 = 0 \quad \text{и} \quad y_0 = 1;$$

• Координаты некоторых точек:

  $$\begin{array}{|c|c|c|c|c|} \hline x & -2 & -1 & 1 & 2 \\ \hline y & 9 & 3 & 3 & 9 \\ \hline \end{array}$$

• График функции:

г) $y = -(x + 2)^2$;

• Область определения: $x \in \mathbb{R}$;
• Множество значений: $y \leq 0$;
• Координаты вершины параболы:

  $$x_0 = -2 \quad \text{и} \quad y_0 = 0;$$

• Координаты некоторых точек:

  $$\begin{array}{|c|c|c|c|c|c|c|} \hline x & -5 & -4 & -3 & -1 & 0 & 1 \\ \hline y & -9 & -4 & -1 & -1 & -4 & -9 \\ \hline \end{array}$$

• График функции:

а) $y = x^2 — 4$

1) Область определения:

• Это квадратичная функция, и квадратичные функции определены для всех действительных чисел. То есть, функция существует для любых значений $x \in \mathbb{R}$.

  Ответ: Область определения: $x \in \mathbb{R}$.

2) Множество значений:

• Для квадратичной функции вида $y = ax^2 + b$, где $a > 0$, график будет иметь форму параболы, открывающейся вверх. Минимальное значение функции будет в вершине параболы, а максимальное значение функции стремится к бесконечности. В данном случае у нас $y = x^2 — 4$, и минимальное значение $y$ будет равно $-4$, когда $x = 0$.

  Ответ: Множество значений: $y \geq -4$.

3) Вершина параболы:

• Для функции $y = x^2 — 4$, вершина параболы будет в точке $(0, -4)$, так как это стандартная форма для квадратичной функции $y = x^2 + b$, где $b = -4$. Парабола симметрична относительно оси $y$.

  Ответ: Координаты вершины параболы: $(x_0, y_0) = (0, -4)$.

4) Координаты некоторых точек:

• Подставим различные значения $x$ в уравнение $y = x^2 — 4$, чтобы получить соответствующие значения $y$:
  • Когда $x = -3$:

    $$y = (-3)^2 — 4 = 9 — 4 = 5$$

    Точка: $(-3, 5)$.

  • Когда $x = -2$:

    $$y = (-2)^2 — 4 = 4 — 4 = 0$$

    Точка: $(-2, 0)$.

  • Когда $x = -1$:

    $$y = (-1)^2 — 4 = 1 — 4 = -3$$

    Точка: $(-1, -3)$.

  • Когда $x = 1$:

    $$y = (1)^2 — 4 = 1 — 4 = -3$$

    Точка: $(1, -3)$.

  • Когда $x = 2$:

    $$y = (2)^2 — 4 = 4 — 4 = 0$$

    Точка: $(2, 0)$.

  • Когда $x = 3$:

    $$y = (3)^2 — 4 = 9 — 4 = 5$$

    Точка: $(3, 5)$.

  Ответ: Координаты некоторых точек:

  $$\begin{array}{|c|c|c|c|c|c|c|} \hline x & -3 & -2 & -1 & 1 & 2 & 3 \\ \hline y & 5 & 0 & -3 & -3 & 0 & 5 \\ \hline \end{array}$$

5) График функции:

График функции $y = x^2 — 4$ представляет собой параболу, которая открывается вверх, с вершиной в точке $(0, -4)$. Она симметрична относительно оси $y$, и значения $y$ увеличиваются по мере того, как $x$ отклоняется от 0 в обе стороны.

График функции:

б) $y = (x — 1)^2$

1) Область определения:

• Как и в предыдущем случае, это квадратичная функция, и она определена для всех значений $x \in \mathbb{R}$.

  Ответ: Область определения: $x \in \mathbb{R}$.

2) Множество значений:

• Это квадратичная функция вида $y = (x — h)^2$, где $h = 1$. Парабола открывается вверх, и её минимальное значение будет равно 0, когда $x = 1$. Функция будет стремиться к бесконечности при $x \to \infty$ или $x \to -\infty$.

  Ответ: Множество значений: $y \geq 0$.

3) Вершина параболы:

• Вершина параболы находится в точке $(x_0, y_0) = (1, 0)$, так как $y = (x — 1)^2$.

  Ответ: Координаты вершины параболы: $(x_0, y_0) = (1, 0)$.

4) Координаты некоторых точек:

• Подставим различные значения $x$ в уравнение $y = (x — 1)^2$:
  • Когда $x = -2$:

    $$y = (-2 — 1)^2 = (-3)^2 = 9$$

    Точка: $(-2, 9)$.

  • Когда $x = -1$:

    $$y = (-1 — 1)^2 = (-2)^2 = 4$$

    Точка: $(-1, 4)$.

  • Когда $x = 0$:

    $$y = (0 — 1)^2 = (-1)^2 = 1$$

    Точка: $(0, 1)$.

  • Когда $x = 2$:

    $$y = (2 — 1)^2 = 1^2 = 1$$

    Точка: $(2, 1)$.

  • Когда $x = 3$:

    $$y = (3 — 1)^2 = 2^2 = 4$$

    Точка: $(3, 4)$.

  • Когда $x = 4$:

    $$y = (4 — 1)^2 = 3^2 = 9$$

    Точка: $(4, 9)$.

  Ответ: Координаты некоторых точек:

  $$\begin{array}{|c|c|c|c|c|c|c|} \hline x & -2 & -1 & 0 & 2 & 3 & 4 \\ \hline y & 9 & 4 & 1 & 1 & 4 & 9 \\ \hline \end{array}$$

5) График функции:

График функции $y = (x — 1)^2$ представляет собой параболу, открывающуюся вверх, с вершиной в точке $(1, 0)$. График симметричен относительно вертикальной прямой $x = 1$.

График функции:

в) $y = 2x^2 + 1$

1) Область определения:

• Эта функция также является квадратичной, и область её определения — все действительные числа, то есть $x \in \mathbb{R}$.

  Ответ: Область определения: $x \in \mathbb{R}$.

2) Множество значений:

• График функции $y = 2x^2 + 1$ — это парабола, открывающаяся вверх, с минимальным значением $y = 1$ при $x = 0$.

  Ответ: Множество значений: $y \geq 1$.

3) Вершина параболы:

• Вершина параболы находится в точке $(0, 1)$, так как у нас функция вида $y = ax^2 + b$, где $a = 2$ и $b = 1$.

  Ответ: Координаты вершины параболы: $(0, 1)$.

4) Координаты некоторых точек:

• Подставим различные значения $x$ в уравнение $y = 2x^2 + 1$:
  • Когда $x = -2$:

    $$y = 2(-2)^2 + 1 = 2 \times 4 + 1 = 9$$

    Точка: $(-2, 9)$.

  • Когда $x = -1$:

    $$y = 2(-1)^2 + 1 = 2 \times 1 + 1 = 3$$

    Точка: $(-1, 3)$.

  • Когда $x = 1$:

    $$y = 2(1)^2 + 1 = 2 \times 1 + 1 = 3$$

    Точка: $(1, 3)$.

  • Когда $x = 2$:

    $$y = 2(2)^2 + 1 = 2 \times 4 + 1 = 9$$

    Точка: $(2, 9)$.

  Ответ: Координаты некоторых точек:

  $$\begin{array}{|c|c|c|c|c|} \hline x & -2 & -1 & 1 & 2 \\ \hline y & 9 & 3 & 3 & 9 \\ \hline \end{array}$$

5) График функции:

График функции $y = 2x^2 + 1$ представляет собой параболу, открывающуюся вверх, с вершиной в точке $(0, 1)$.

График функции:

г) $y = -(x + 2)^2$

1) Область определения:

• Это также квадратичная функция, и она определена для всех действительных значений $x \in \mathbb{R}$.

  Ответ: Область определения: $x \in \mathbb{R}$.

2) Множество значений:

• Эта функция представляет собой параболу, открывающуюся вниз, с максимальным значением $y = 0$ при $x = -2$.

  Ответ: Множество значений: $y \leq 0$.

3) Вершина параболы:

• Вершина параболы будет в точке $(x_0, y_0) = (-2, 0)$, так как функция имеет вид $y = -(x + 2)^2$.

  Ответ: Координаты вершины параболы: $(x_0, y_0) = (-2, 0)$.

4) Координаты некоторых точек:

• Подставим различные значения $x$ в уравнение $y = -(x + 2)^2$:
  • Когда $x = -5$:

    $$y = -(-5 + 2)^2 = -(-3)^2 = -9$$

    Точка: $(-5, -9)$.

  • Когда $x = -4$:

    $$y = -(-4 + 2)^2 = -(-2)^2 = -4$$

    Точка: $(-4, -4)$.

  • Когда $x = -3$:

    $$y = -(-3 + 2)^2 = -(1)^2 = -1$$

    Точка: $(-3, -1)$.

  • Когда $x = -1$:

    $$y = -(-1 + 2)^2 = -(1)^2 = -1$$

    Точка: $(-1, -1)$.

  • Когда $x = 0$:

    $$y = -(0 + 2)^2 = -(2)^2 = -4$$

    Точка: $(0, -4)$.

  • Когда $x = 1$:

    $$y = -(1 + 2)^2 = -(3)^2 = -9$$

    Точка: $(1, -9)$.

  Ответ: Координаты некоторых точек:

  $$\begin{array}{|c|c|c|c|c|c|c|} \hline x & -5 & -4 & -3 & -1 & 0 & 1 \\ \hline y & -9 & -4 & -1 & -1 & -4 & -9 \\ \hline \end{array}$$

5) График функции:

График функции $y = -(x + 2)^2$ представляет собой параболу, открывающуюся вниз, с вершиной в точке $(-2, 0)$.

График функции: