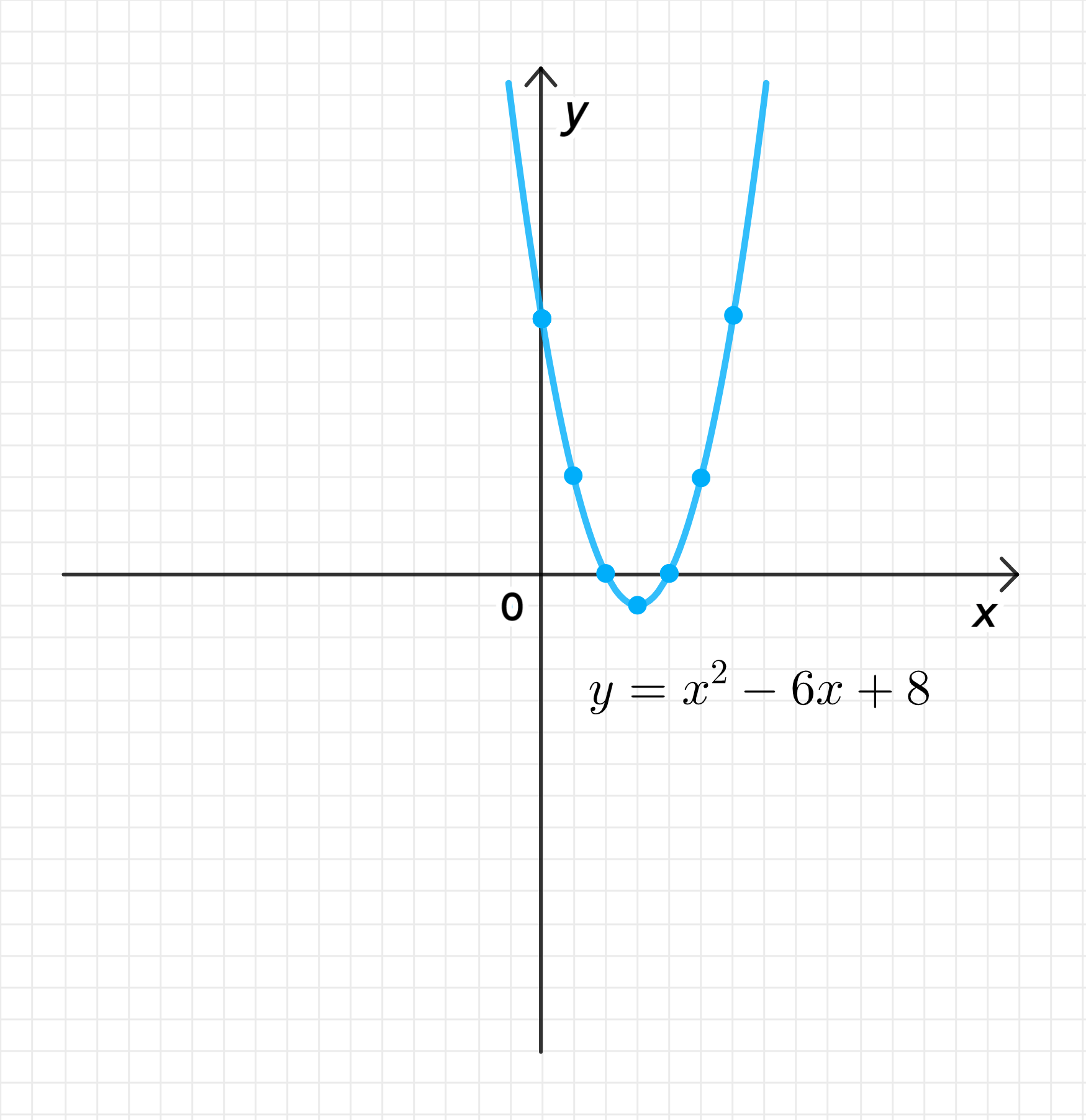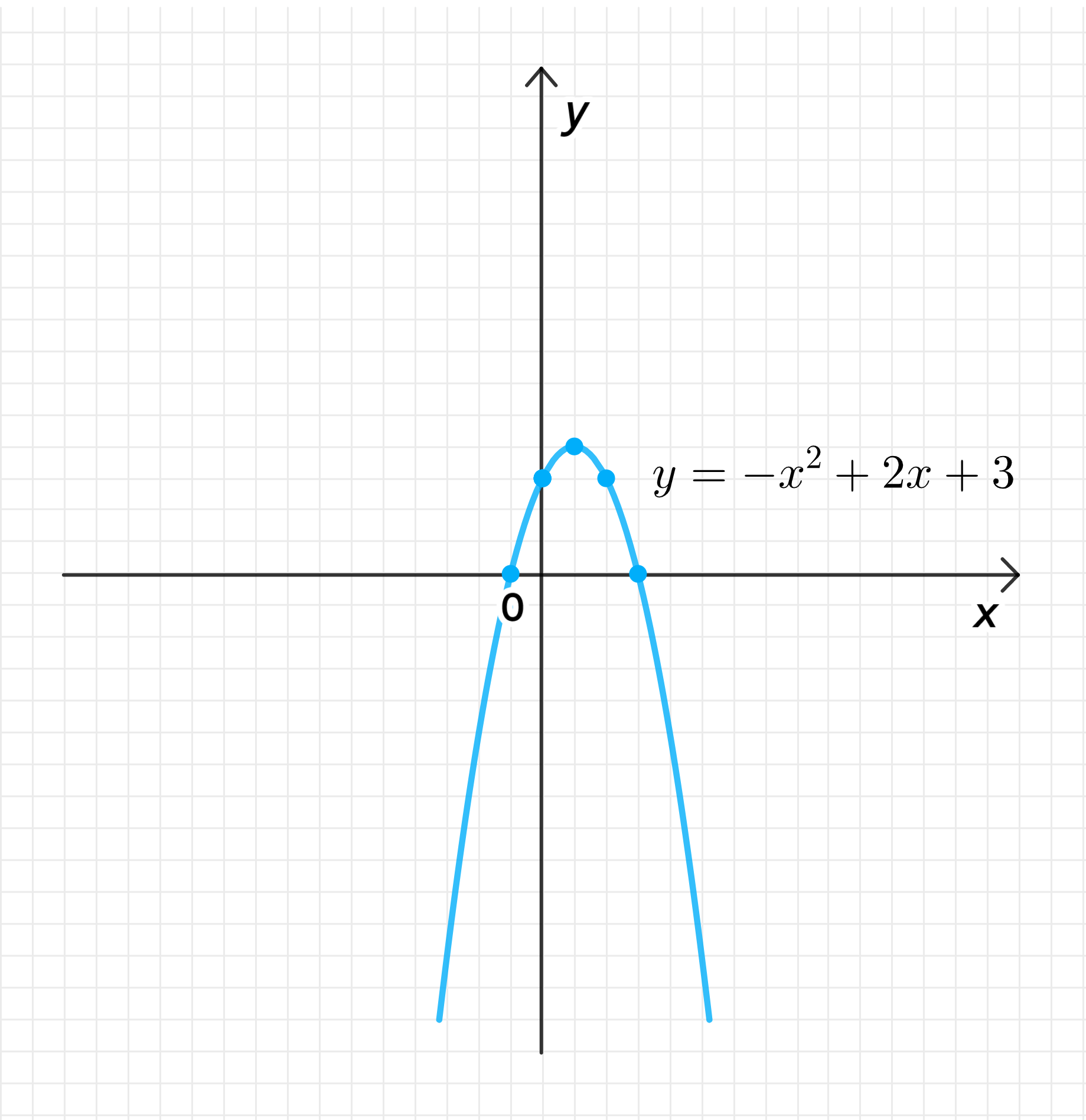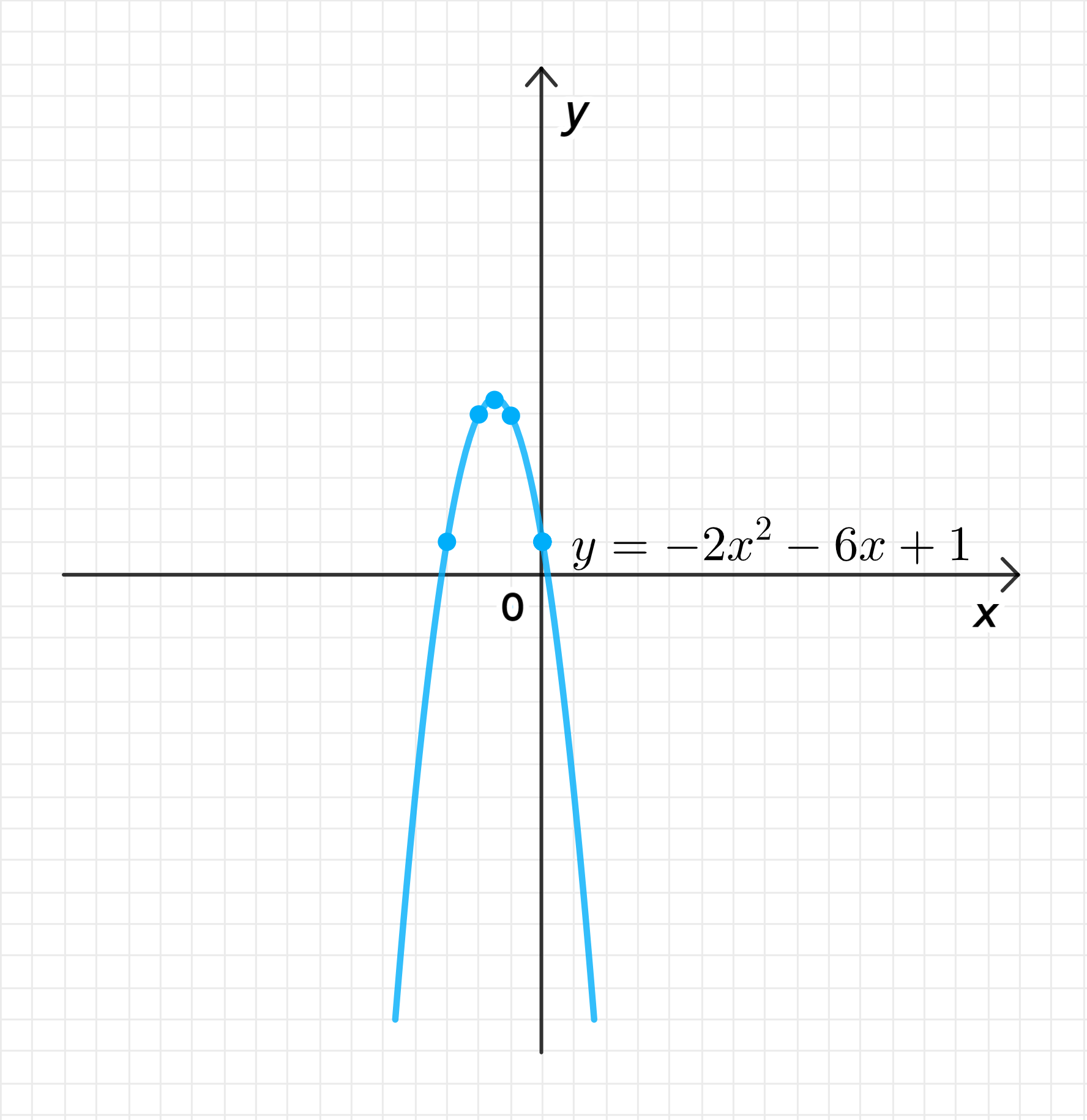Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 7.15 Профильный Уровень Мордкович — Подробные Ответы
а) ;
б) ;
в) ;
г)
а) ;
Координаты вершины параболы:
Область определения: ;
Множество значений: ;
Координаты некоторых точек:
График функции:
б) ;
Координаты вершины параболы:
Область определения: ;
Множество значений: ;
Координаты некоторых точек:
График функции:
в) ;
Координаты вершины параболы:
Область определения: ;
Множество значений: ;
Координаты некоторых точек:
График функции:
г) ;
Координаты вершины параболы:
Область определения: ;
Множество значений: ;
Координаты некоторых точек:
График функции:
а) :
Координаты вершины параболы:
Парабола имеет вид , где , , и .
Для нахождения координат вершины используем формулы:
Подставляем значение в уравнение функции для нахождения :
Таким образом, координаты вершины параболы: .
Область определения:
Поскольку функция является полиномиальной, она определена для всех . Следовательно, область определения:
Множество значений:
Парабола открывается вверх (так как ), и ее минимальное значение достигается в вершине. Так как , то множество значений будет:
Координаты некоторых точек:
Для различных значений , вычислим соответствующие значения :
График функции:
б) :
Координаты вершины параболы:
Для функции , где , , и , находим вершину:
Подставляем значение в уравнение функции для нахождения :
Таким образом, координаты вершины параболы: .
Область определения:
Поскольку функция полиномиальная, область определения .
Множество значений:
Парабола открывается вниз (так как ), и ее максимальное значение достигается в вершине. Следовательно, множество значений будет:
Координаты некоторых точек:
Для различных значений , вычислим соответствующие значения :
График функции:
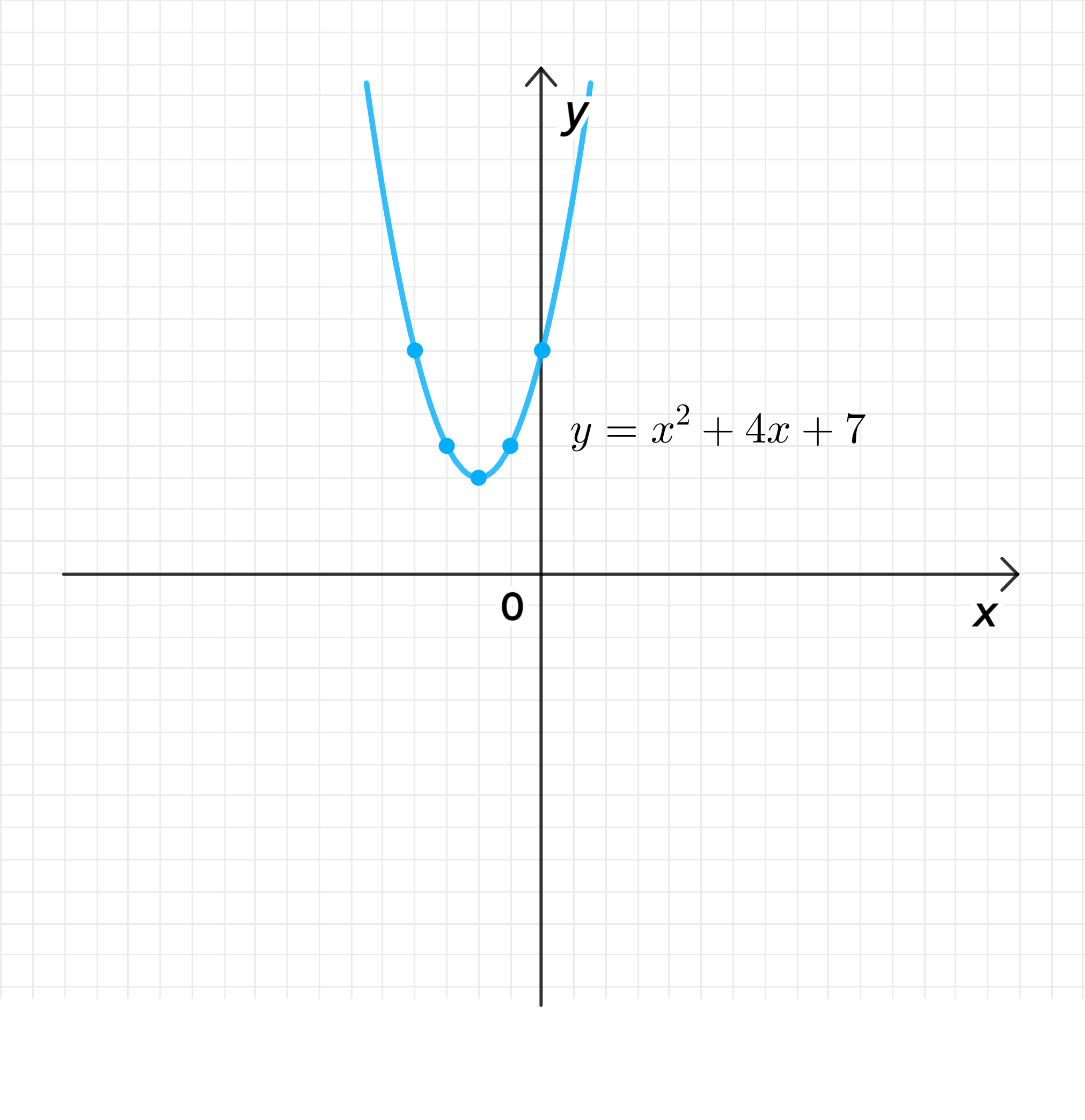
в) :
Координаты вершины параболы:
Для функции , где , , и , находим вершину:
Подставляем значение в уравнение функции для нахождения :
Таким образом, координаты вершины параболы: .
Область определения:
Поскольку функция полиномиальная, область определения .
Множество значений:
Парабола открывается вверх (так как ), и ее минимальное значение достигается в вершине. Следовательно, множество значений будет:
Координаты некоторых точек:
Для различных значений , вычислим соответствующие значения :
График функции:
г) :
Координаты вершины параболы:
Для функции , где , , и , находим вершину:
Подставляем значение в уравнение функции для нахождения :
Таким образом, координаты вершины параболы: .
Область определения:
Поскольку функция полиномиальная, область определения .
Множество значений:
Парабола открывается вниз (так как ), и ее максимальное значение достигается в вершине. Следовательно, множество значений будет:
Координаты некоторых точек:
Для различных значений , вычислим соответствующие значения :
График функции: