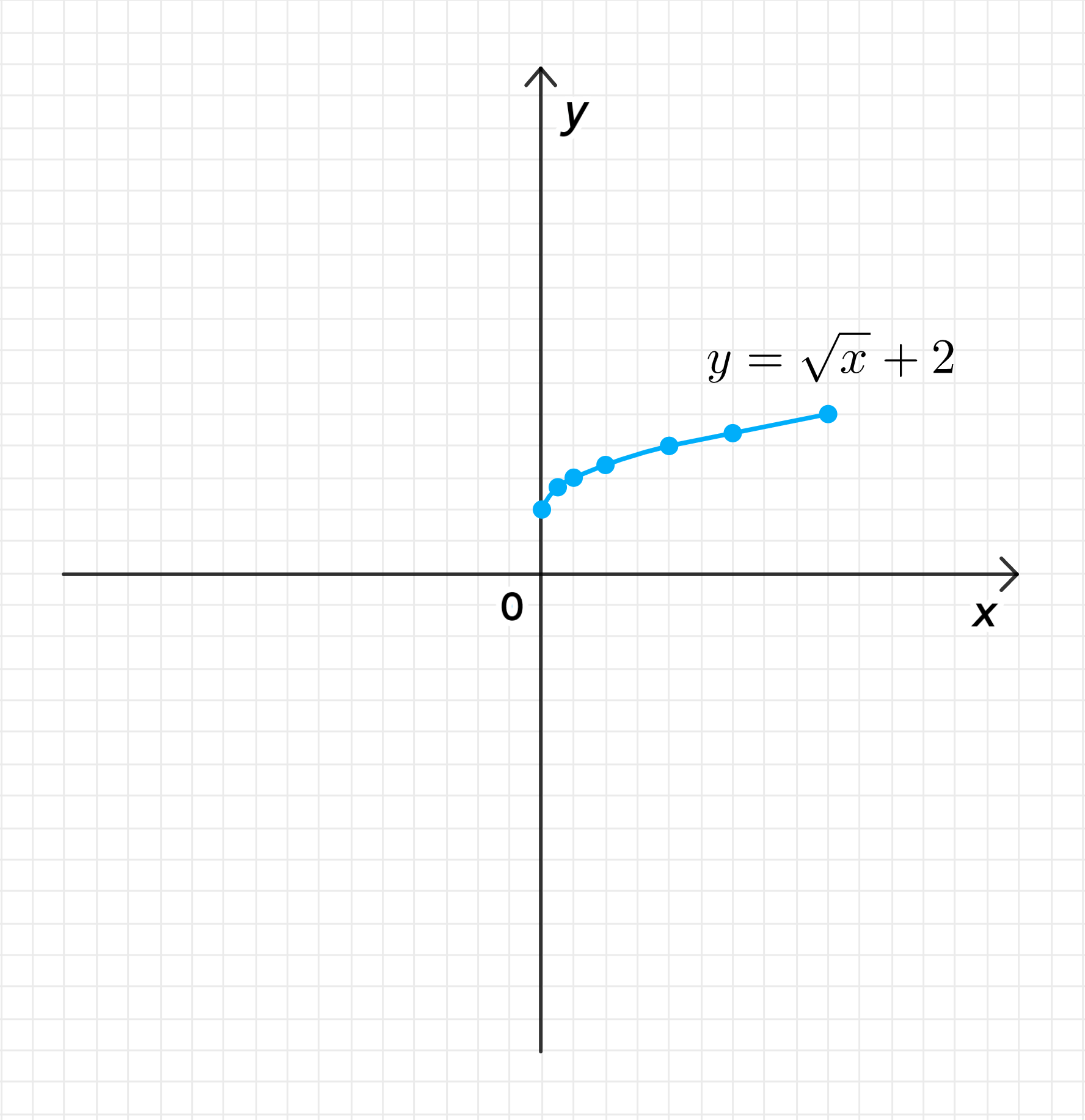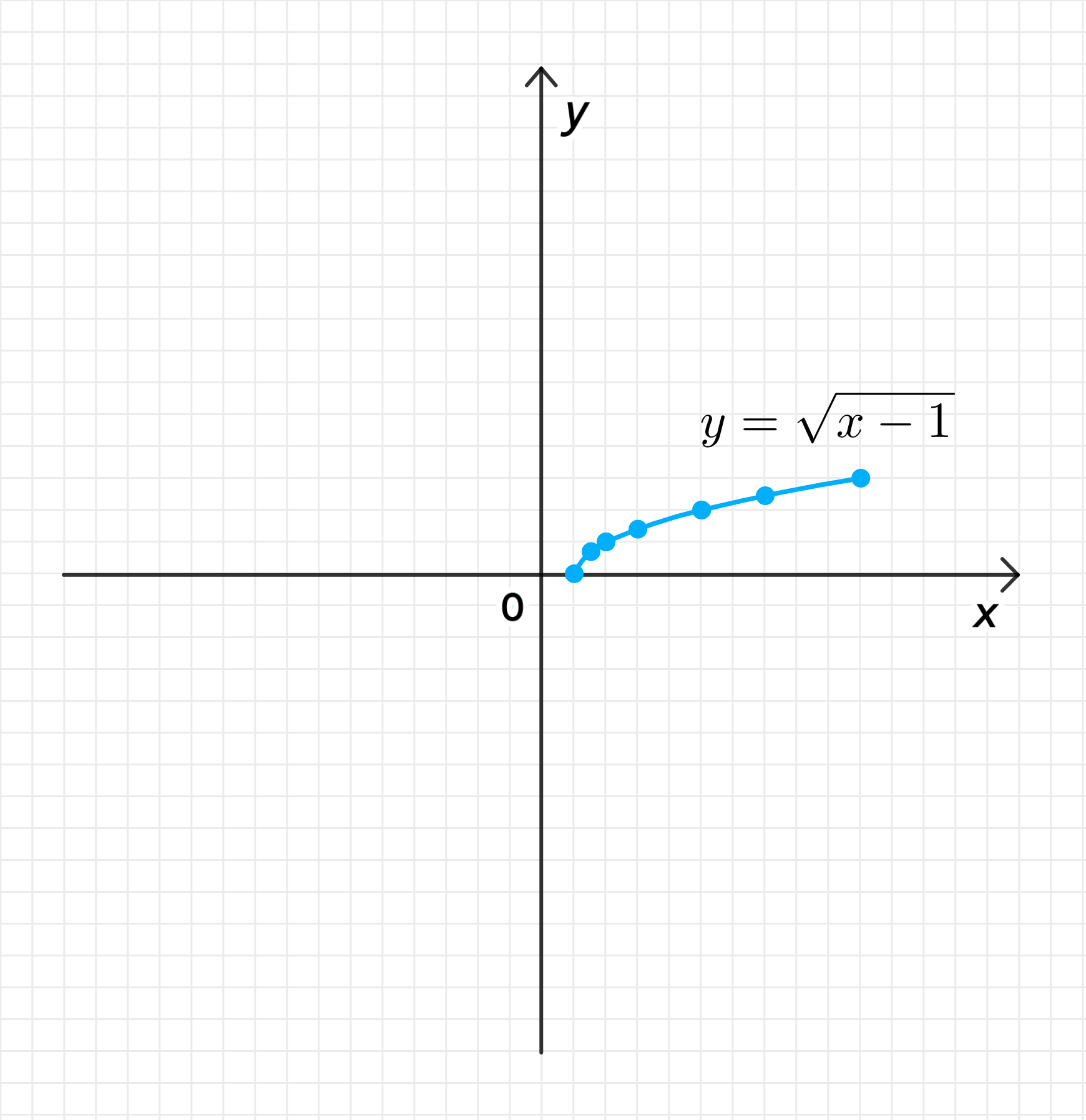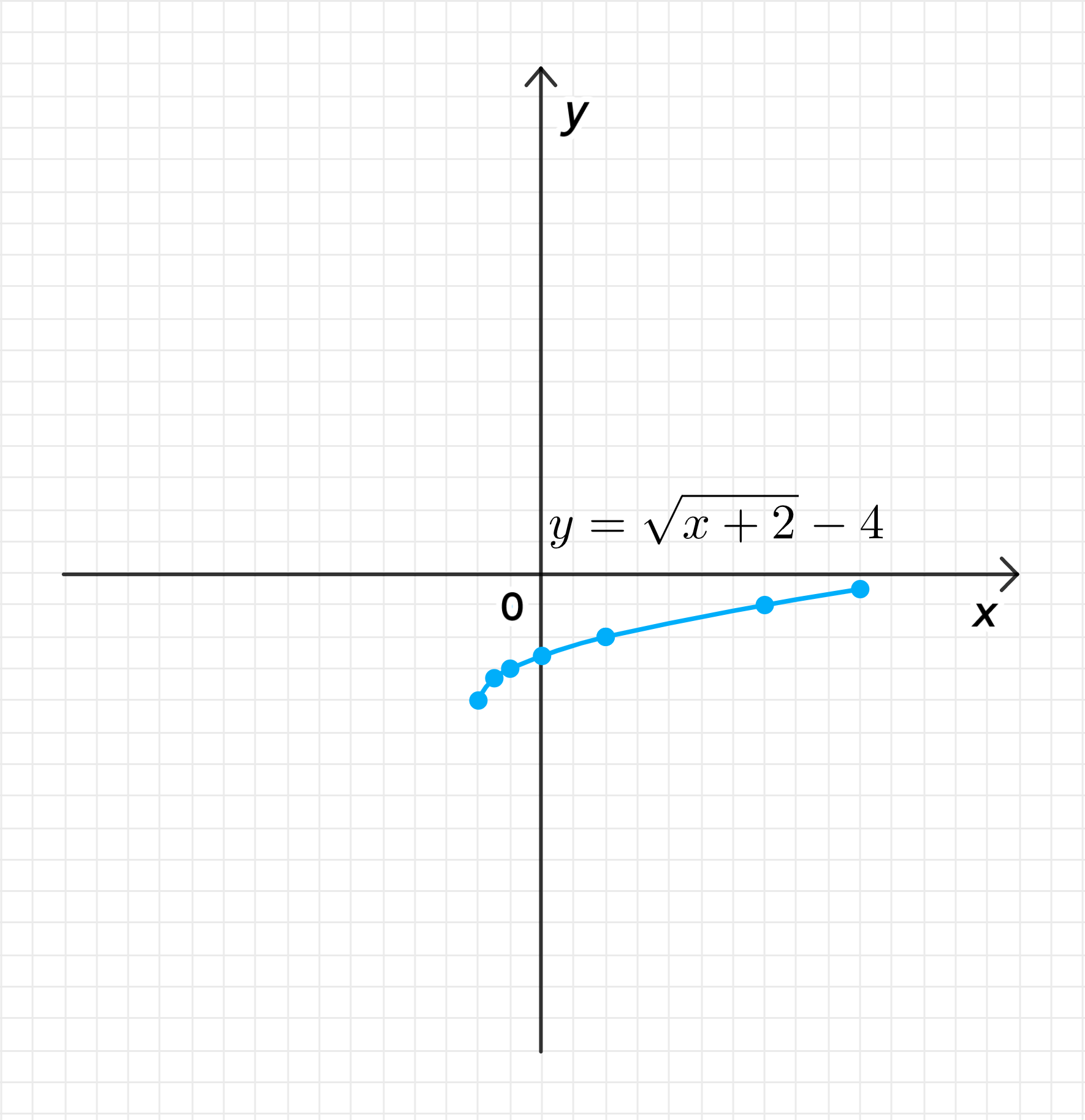ГДЗ по Алгебре 10 Класс Номер 7.16 Профильный Уровень Мордкович — Подробные Ответы

а) $y=\sqrt{x}$

б) $y=\sqrt{x}+2$

в) $y=\sqrt{x-1}$

г) $y=\sqrt{x+2}-4$

а) $y = \sqrt{x}$

Область определения: $x \geq 0$;

Множество значений: $y \geq 0$;

Координаты вершины ветви параболы:

$x_0 = 0$ и $y_0 = 0$;

Координаты некоторых точек:

График функции:

б) $y = \sqrt{x} + 2$

Область определения: $x \geq 0$;

Множество значений: $y \geq 2$;

Координаты вершины ветви параболы:

$x_0 = 0$ и $y_0 = 2$;

Координаты некоторых точек:

График функции:

в) $y = \sqrt{x — 1}$

Область определения: $x \geq 1$;

Множество значений: $y \geq 0$;

Координаты вершины ветви параболы:

$x_0 = 1$ и $y_0 = 0$;

Координаты некоторых точек:

График функции:

г) $y = \sqrt{x + 2} — 4$

Область определения: $x \geq -2$;

Множество значений: $y \geq -4$;

Координаты вершины ветви параболы:

$x_0 = -2$ и $y_0 = -4$;

Координаты некоторых точек:

График функции:

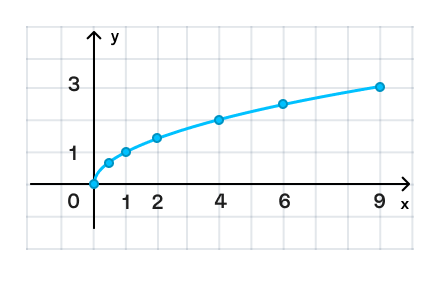
а) Функция $y = \sqrt{x}$

1.1. Область определения

Функция $\sqrt{x}$ определена для всех $x \geq 0$, так как извлечение квадратного корня из отрицательных чисел в действительных числах невозможно. Таким образом, область определения:

$$D = \{x \in \mathbb{R} \mid x \geq 0\}$$

1.2. Множество значений

Так как извлечение квадратного корня из любого неотрицательного числа всегда даёт неотрицательный результат, то множество значений функции будет:

$$M = \{y \in \mathbb{R} \mid y \geq 0\}$$

1.3. Вершина графика

Вершина графика — это точка, в которой функция начинает своё возрастание. Для функции $y = \sqrt{x}$, это точка $x_0 = 0$, $y_0 = \sqrt{0} = 0$. Таким образом, координаты вершины:

$$(x_0, y_0) = (0, 0)$$

1.4. Координаты некоторых точек

Вычислим несколько значений функции для различных значений $x$:

• Когда $x = 0$, $y = \sqrt{0} = 0$
• Когда $x = 1$, $y = \sqrt{1} = 1$
• Когда $x = 4$, $y = \sqrt{4} = 2$
• Когда $x = 9$, $y = \sqrt{9} = 3$

1.5. График функции

б) Функция $y = \sqrt{x} + 2$

2.1. Область определения

Функция $y = \sqrt{x} + 2$ имеет такую же область определения, как и $y = \sqrt{x}$, так как $\sqrt{x}$ определена для $x \geq 0$. Таким образом:

$$D = \{x \in \mathbb{R} \mid x \geq 0\}$$

2.2. Множество значений

Добавление числа 2 ко всем значениям функции $\sqrt{x}$ сдвигает её график вверх на 2 единицы. Множество значений будет $y \geq 2$, так как минимальное значение $y$ будет равно 2, когда $x = 0$.

$$M = \{y \in \mathbb{R} \mid y \geq 2\}$$

2.3. Вершина графика

Вершина функции $y = \sqrt{x} + 2$ находится в точке $x_0 = 0$, $y_0 = \sqrt{0} + 2 = 2$. Таким образом:

$$(x_0, y_0) = (0, 2)$$

2.4. Координаты некоторых точек

Вычислим несколько значений функции для различных значений $x$:

• Когда $x = 0$, $y = \sqrt{0} + 2 = 2$
• Когда $x = 1$, $y = \sqrt{1} + 2 = 3$
• Когда $x = 4$, $y = \sqrt{4} + 2 = 4$
• Когда $x = 9$, $y = \sqrt{9} + 2 = 5$

2.5. График функции

в) Функция $y = \sqrt{x — 1}$

3.1. Область определения

Для функции $y = \sqrt{x — 1}$ область определения будет $x \geq 1$, так как извлечение квадратного корня из числа, меньшего 1, даёт комплексные значения.

$$D = \{x \in \mathbb{R} \mid x \geq 1\}$$

3.2. Множество значений

Как и в случае с $y = \sqrt{x}$, данная функция будет принимать все неотрицательные значения, начиная с 0. Множество значений:

$$M = \{y \in \mathbb{R} \mid y \geq 0\}$$

3.3. Вершина графика

Вершина графика функции $y = \sqrt{x — 1}$ находится в точке $x_0 = 1$, $y_0 = \sqrt{1 — 1} = 0$. Таким образом:

$$(x_0, y_0) = (1, 0)$$

3.4. Координаты некоторых точек

Вычислим несколько значений функции для различных значений $x$:

• Когда $x = 1$, $y = \sqrt{1 — 1} = 0$
• Когда $x = 2$, $y = \sqrt{2 — 1} = 1$
• Когда $x = 5$, $y = \sqrt{5 — 1} = 2$
• Когда $x = 10$, $y = \sqrt{10 — 1} = 3$

3.5. График функции

г) Функция $y = \sqrt{x + 2} — 4$

4.1. Область определения

Для функции $y = \sqrt{x + 2} — 4$ область определения будет $x \geq -2$, так как для извлечения квадратного корня из выражения $x + 2$ необходимо, чтобы $x + 2 \geq 0$, то есть $x \geq -2$.

$$D = \{x \in \mathbb{R} \mid x \geq -2\}$$

4.2. Множество значений

Добавление числа -4 ко всем значениям функции $\sqrt{x + 2}$ сдвигает её график вниз на 4 единицы. Множество значений будет $y \geq -4$, так как минимальное значение $y$ будет равно -4, когда $x = -2$.

$$M = \{y \in \mathbb{R} \mid y \geq -4\}$$

4.3. Вершина графика

Вершина графика функции $y = \sqrt{x + 2} — 4$ находится в точке $x_0 = -2$, $y_0 = \sqrt{-2 + 2} — 4 = -4$. Таким образом:

$$(x_0, y_0) = (-2, -4)$$

4.4. Координаты некоторых точек

Вычислим несколько значений функции для различных значений $x$:

• Когда $x = -2$, $y = \sqrt{-2 + 2} — 4 = -4$
• Когда $x = -1$, $y = \sqrt{-1 + 2} — 4 = -3$
• Когда $x = 2$, $y = \sqrt{2 + 2} — 4 = -2$
• Когда $x = 7$, $y = \sqrt{7 + 2} — 4 = -1$

4.5. График функции