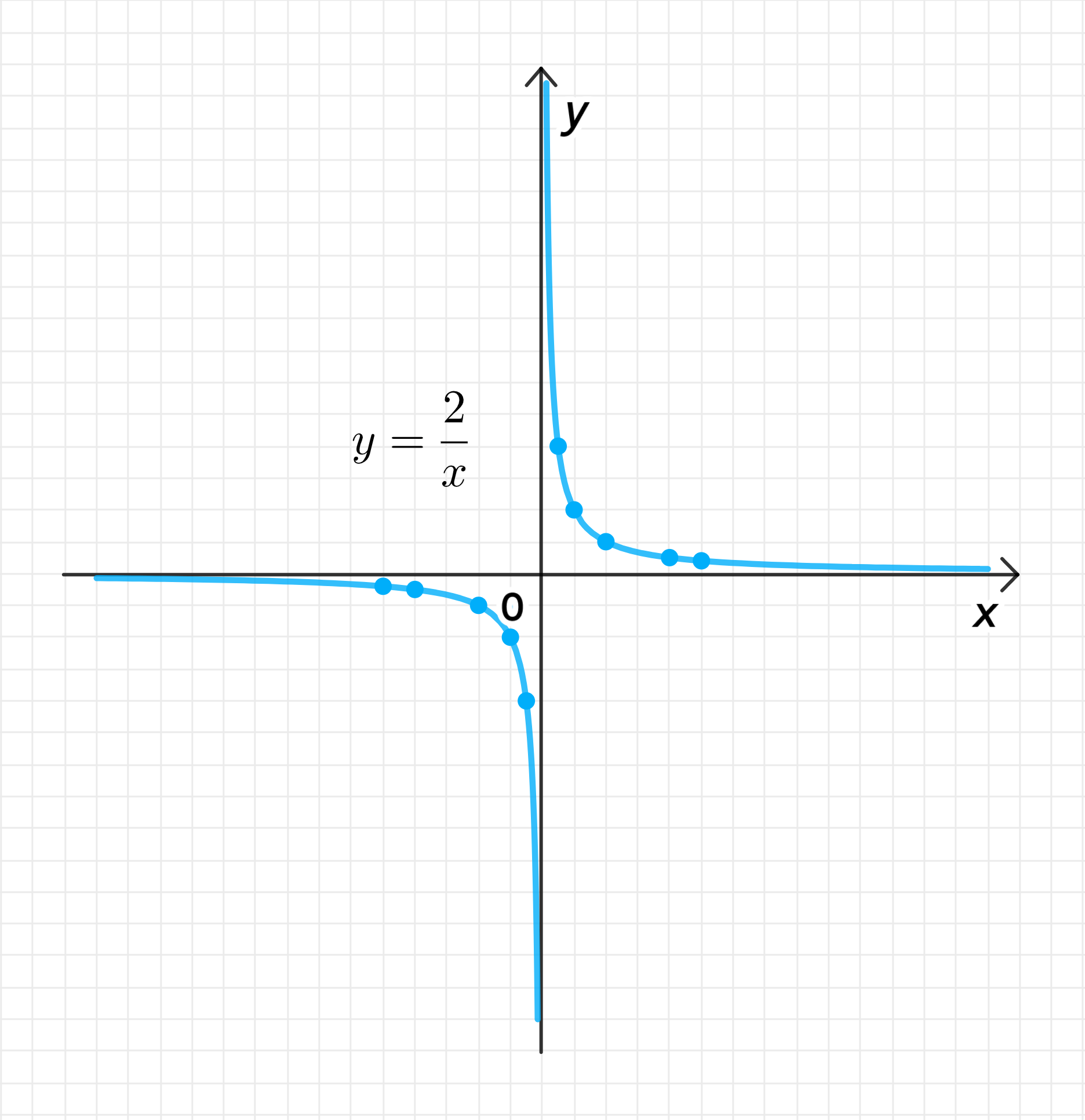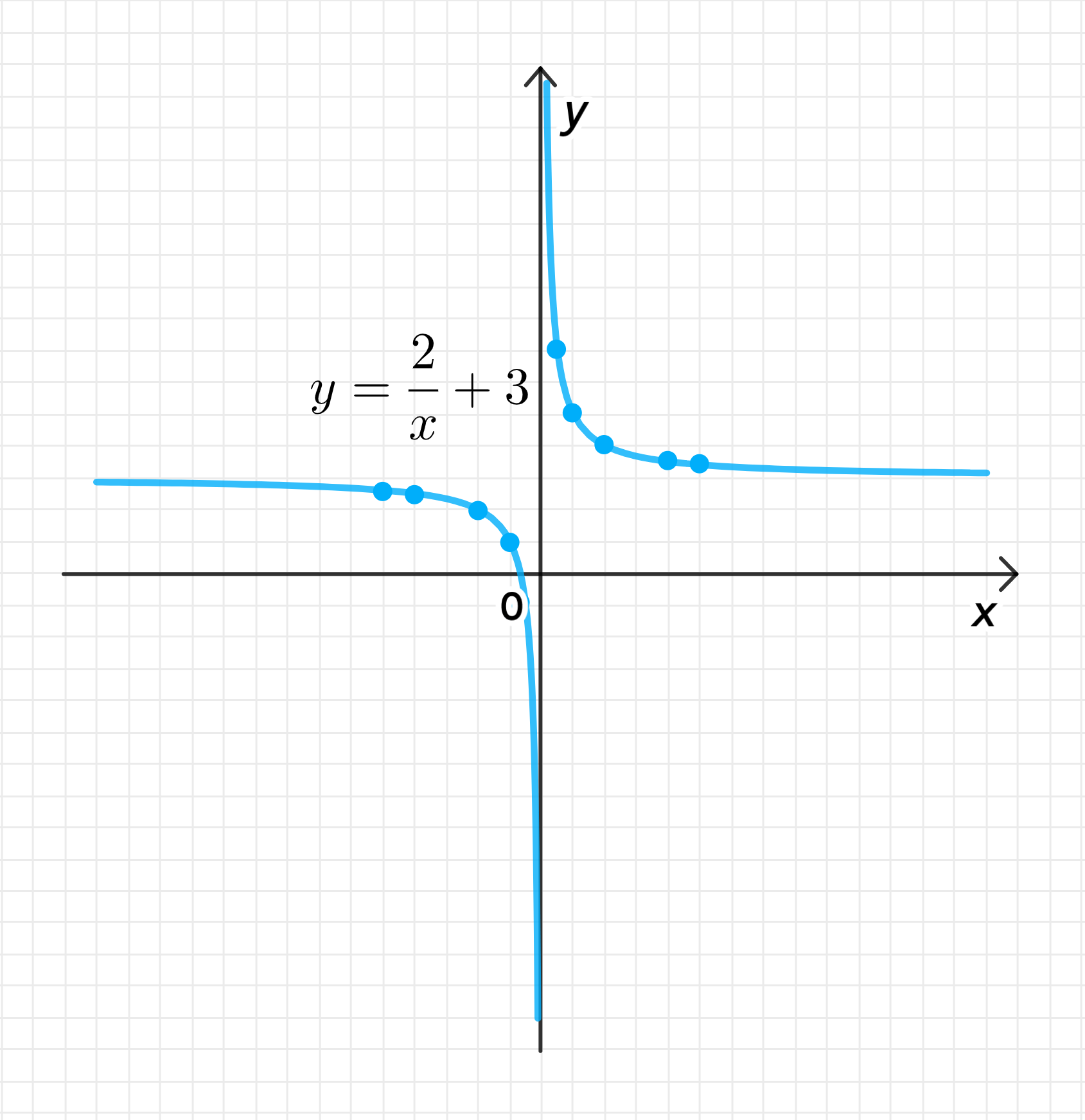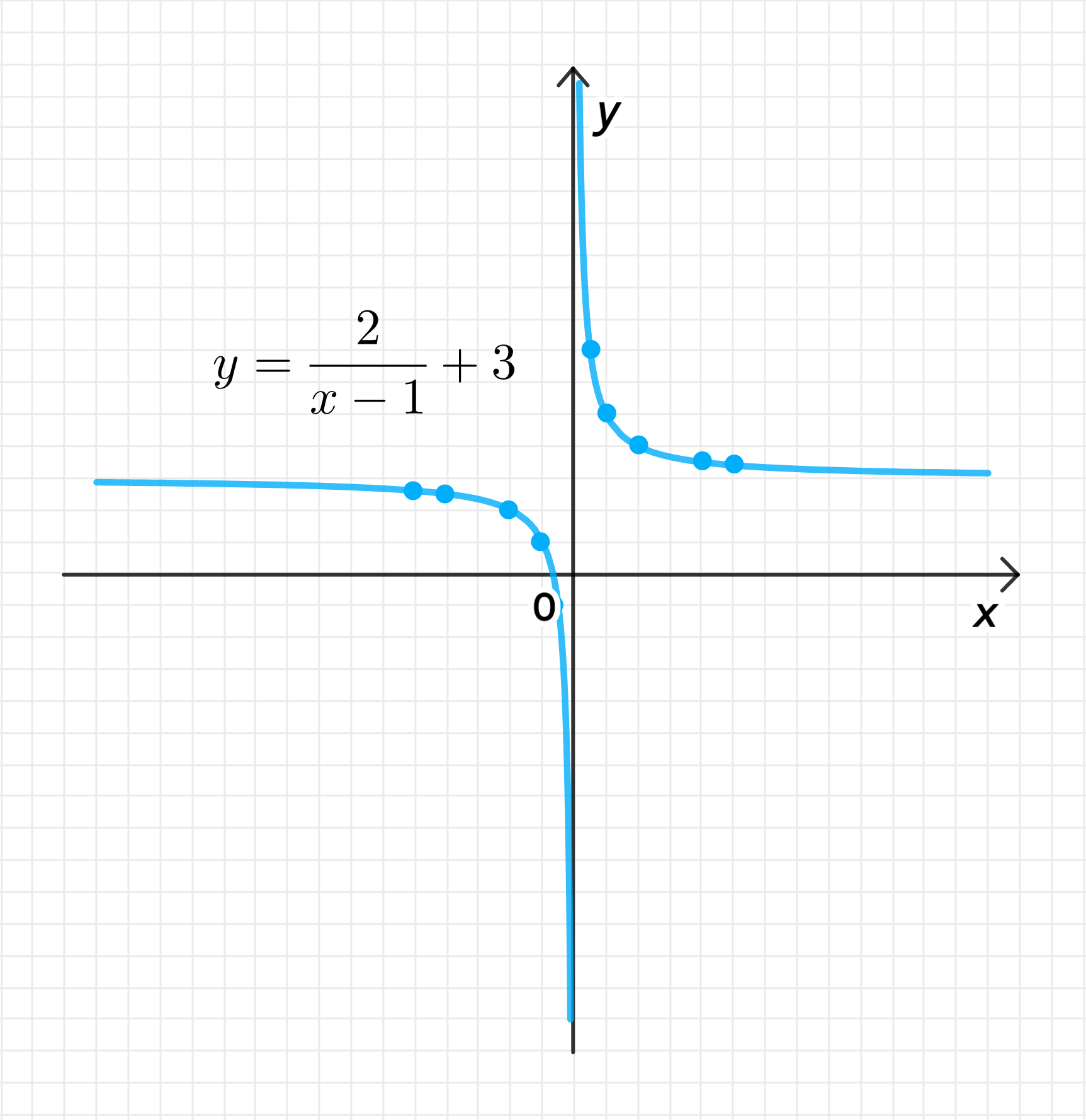ГДЗ по Алгебре 10 Класс Номер 7.17 Профильный Уровень Мордкович — Подробные Ответы

а) $y=\frac{2}{x}$

б) $y=\frac{2}{x-1}$

в) $y=\frac{2}{x}+3$

г) $y=\frac{2}{x-1}+3$

а) $y = \frac{2}{x}$

Область определения: $x \neq 0$;

Множество значений: $y \neq 0$;

Уравнения асимптот гиперболы:

$x = 0$ и $y = 0$;

Координаты некоторых точек:

График функции:

б) $y = \frac{2}{x — 1}$

Область определения: $x \neq 1$;

Множество значений: $y \neq 0$;

Уравнения асимптот гиперболы:

$x = 1$ и $y = 0$;

Координаты некоторых точек:

График функции:

в) $y = \frac{2}{x} + 3$

Область определения: $x \neq 0$;

Множество значений: $y \neq 3$;

Уравнения асимптот гиперболы:

$x = 0$ и $y = 3$;

Координаты некоторых точек:

График функции:

г) $y = \frac{2}{x — 1} + 3$

Область определения: $x \neq 1$;

Множество значений: $y \neq 3$;

Уравнения асимптот гиперболы:

$x = 1$ и $y = 3$;

Координаты некоторых точек:

График функции:

а) Функция $y = \frac{2}{x}$

1.1. Область определения

Область определения функции — это множество значений $x$, при которых выражение $\frac{2}{x}$ определено. Для этого знаменатель не должен равняться нулю, так как деление на ноль невозможно в действительных числах. Таким образом:

$$x \neq 0$$

Следовательно, область определения функции:

$$D = \{x \in \mathbb{R} \mid x \neq 0\}$$

1.2. Множество значений

Функция $y = \frac{2}{x}$ принимает все значения, кроме нуля. При $x \to 0^+$ (при $x$ стремящемся к нулю справа), $y$ стремится к бесконечности. При $x \to 0^-$ (при $x$ стремящемся к нулю слева), $y$ стремится к минус бесконечности. Таким образом, функция не может быть равна нулю, то есть:

$$M = \{y \in \mathbb{R} \mid y \neq 0\}$$

1.3. Асимптоты

• Вертикальная асимптота: когда $x \to 0$, функция стремится к бесконечности. Следовательно, есть вертикальная асимптота $x = 0$.
• Горизонтальная асимптота: когда $x \to \infty$ или $x \to -\infty$, функция стремится к нулю. Следовательно, есть горизонтальная асимптота $y = 0$.

Уравнения асимптот гиперболы:

• $x = 0$
• $y = 0$

1.4. Координаты некоторых точек

Вычислим несколько значений функции для различных значений $x$:

• Когда $x = -2$, $y = \frac{2}{-2} = -1$
• Когда $x = -1$, $y = \frac{2}{-1} = -2$
• Когда $x = 1$, $y = \frac{2}{1} = 2$
• Когда $x = 2$, $y = \frac{2}{2} = 1$

1.5. График функции

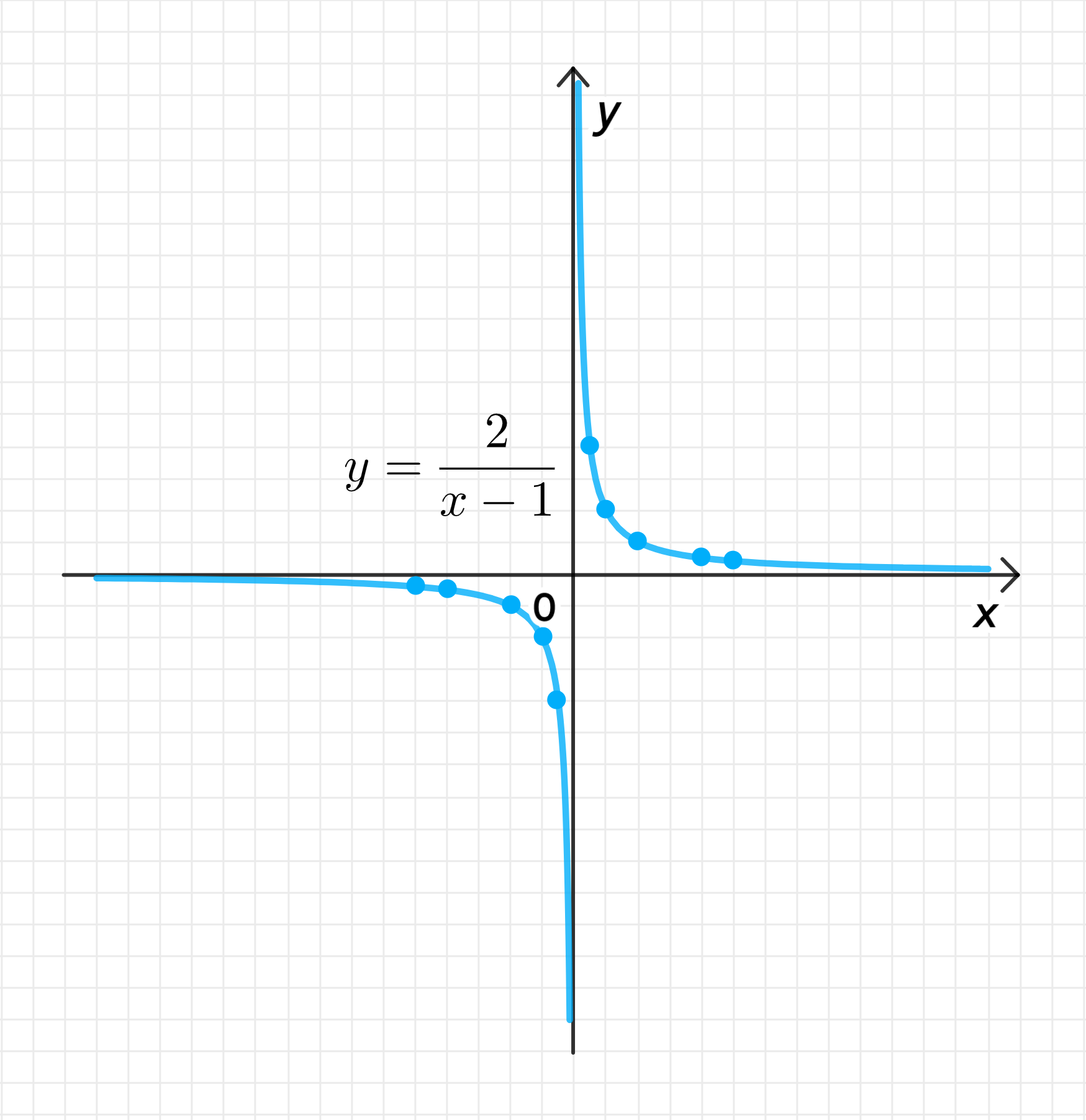
б) Функция $y = \frac{2}{x — 1}$

2.1. Область определения

Функция $y = \frac{2}{x — 1}$ определена, когда знаменатель не равен нулю. Таким образом, область определения:

$$x — 1 \neq 0 \quad \Rightarrow \quad x \neq 1$$

Следовательно, область определения функции:

$$D = \{x \in \mathbb{R} \mid x \neq 1\}$$

2.2. Множество значений

Как и в предыдущем случае, функция $y = \frac{2}{x — 1}$ не может быть равна нулю, поскольку деление на ноль невозможно. Множество значений:

$$M = \{y \in \mathbb{R} \mid y \neq 0\}$$

2.3. Асимптоты

• Вертикальная асимптота: функция $y = \frac{2}{x — 1}$ имеет вертикальную асимптоту, когда $x \to 1$, так как выражение $\frac{2}{x — 1}$ стремится к бесконечности. Следовательно, уравнение вертикальной асимптоты:

$$x = 1$$

• Горизонтальная асимптота: когда $x \to \infty$ или $x \to -\infty$, функция стремится к нулю. Следовательно, уравнение горизонтальной асимптоты:

$$y = 0$$

2.4. Координаты некоторых точек

Вычислим несколько значений функции для различных значений $x$:

• Когда $x = -1$, $y = \frac{2}{-1 — 1} = -1$
• Когда $x = 0$, $y = \frac{2}{0 — 1} = -2$
• Когда $x = 2$, $y = \frac{2}{2 — 1} = 2$
• Когда $x = 3$, $y = \frac{2}{3 — 1} = 1$

2.5. График функции

в) Функция $y = \frac{2}{x} + 3$

3.1. Область определения

Область определения функции аналогична функции $y = \frac{2}{x}$, так как деление на ноль по-прежнему невозможно. Таким образом, область определения:

$$D = \{x \in \mathbb{R} \mid x \neq 0\}$$

3.2. Множество значений

Добавление 3 к функции $y = \frac{2}{x}$ сдвигает график функции вверх на 3 единицы. Следовательно, множество значений:

$$M = \{y \in \mathbb{R} \mid y \neq 3\}$$

3.3. Асимптоты

• Вертикальная асимптота: вертикальная асимптота остаётся в точке $x = 0$, как и для функции $y = \frac{2}{x}$.
• Горизонтальная асимптота: так как добавление константы 3 не влияет на горизонтальную асимптоту, она остаётся на уровне $y = 3$.

Уравнения асимптот гиперболы:

• $x = 0$
• $y = 3$

3.4. Координаты некоторых точек

Вычислим несколько значений функции для различных значений $x$:

• Когда $x = -2$, $y = \frac{2}{-2} + 3 = 2$
• Когда $x = -1$, $y = \frac{2}{-1} + 3 = 1$
• Когда $x = 1$, $y = \frac{2}{1} + 3 = 5$
• Когда $x = 2$, $y = \frac{2}{2} + 3 = 4$

3.5. График функции

г) Функция $y = \frac{2}{x — 1} + 3$

4.1. Область определения

Как и для функции $y = \frac{2}{x — 1}$, область определения функции $y = \frac{2}{x — 1} + 3$ такая же:

$$D = \{x \in \mathbb{R} \mid x \neq 1\}$$

4.2. Множество значений

Добавление 3 к функции $y = \frac{2}{x — 1}$ сдвигает график функции вверх на 3 единицы. Следовательно, множество значений:

$$M = \{y \in \mathbb{R} \mid y \neq 3\}$$

4.3. Асимптоты

• Вертикальная асимптота: вертикальная асимптота остаётся в точке $x = 1$, как и для функции $y = \frac{2}{x — 1}$.
• Горизонтальная асимптота: горизонтальная асимптота остаётся на уровне $y = 3$, как и для функции $y = \frac{2}{x} + 3$.

Уравнения асимптот гиперболы:

• $x = 1$
• $y = 3$

4.4. Координаты некоторых точек

Вычислим несколько значений функции для различных значений $x$:

• Когда $x = -1$, $y = \frac{2}{-1 — 1} + 3 = 2$
• Когда $x = 0$, $y = \frac{2}{0 — 1} + 3 = 1$
• Когда $x = 2$, $y = \frac{2}{2 — 1} + 3 = 5$
• Когда $x = 3$, $y = \frac{2}{3 — 1} + 3 = 4$

4.5. График функции