ГДЗ по Алгебре 10 Класс Номер 7.19 Профильный Уровень Мордкович — Подробные Ответы

а) $y = \sqrt[3]{x}$;

б) $y = |\sqrt[3]{x} — 1|$

а) $y = \sqrt[3]{x}$;

Область определения: $x \in \mathbb{R}$;

Множество значений: $y \in \mathbb{R}$;

Координаты вершины параболы:

$x_0 = 0$ и $y_0 = 0$;

Координаты некоторых точек:

График функции:

б) $y = |\sqrt[3]{x} — 1|$;

Рассмотрим функцию $y = \sqrt[3]{x} — 1$:

Область определения: $x \in \mathbb{R}$;

Множество значений: $y \in \mathbb{R}$;

Координаты вершины параболы:

$x_0 = 0$ и $y_0 = -1$;

Построим график функции $y = \sqrt[3]{x} — 1$, а затем отразим относительно оси абсцисс его часть, лежащую под этой осью.

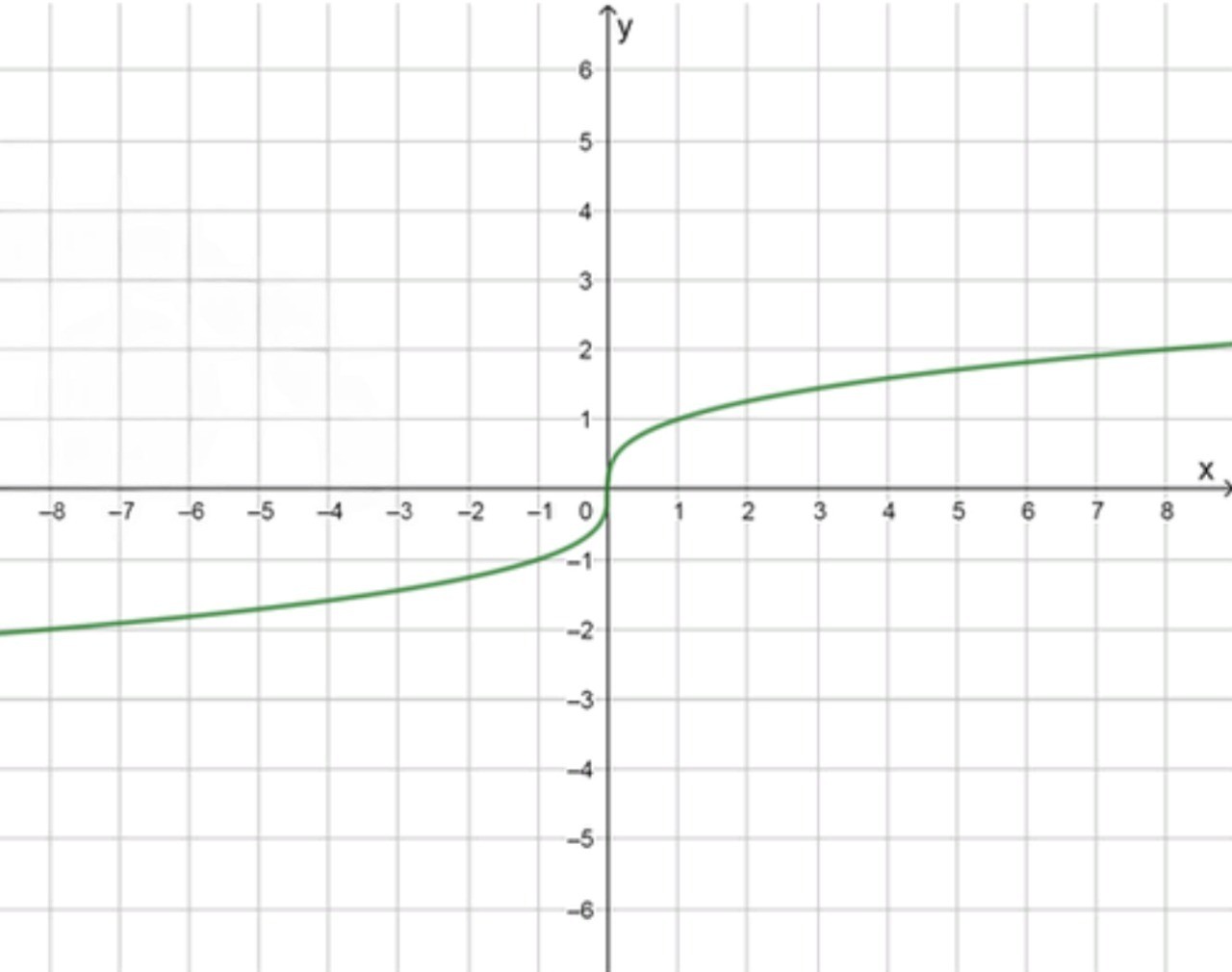
а) $y = \sqrt[3]{x}$

1. Область определения:

• Кубический корень из $x$ определён для всех действительных чисел, поскольку для любого $x \in \mathbb{R}$ существует его кубический корень, и это число будет также действительным (например, для отрицательных чисел кубический корень также существует и равен отрицательному числу).
• Область определения: $x \in \mathbb{R}$.

2. Множество значений:

• Кубический корень из $x$ может быть любым действительным числом, как положительным, так и отрицательным, в зависимости от значения $x$. Например:
  • Если $x = 8$, то $y = \sqrt[3]{8} = 2$;
  • Если $x = -8$, то $y = \sqrt[3]{-8} = -2$;
  • Если $x = 0$, то $y = \sqrt[3]{0} = 0$.
• Множество значений: $y \in \mathbb{R}$, то есть для всех значений $x$ функция принимает все значения на действительной оси.

3. Координаты вершины:

• Для функции $y = \sqrt[3]{x}$ нет традиционной «вершины» в смысле функции с модулями или параболы, так как эта функция монотонно возрастает, и её график имеет форму «S». Однако можно выделить важную точку, где функция пересекает обе оси (начало координат):
  • При $x = 0$, $y = \sqrt[3]{0} = 0$. Это точка пересечения графика с началом координат.
• Координаты вершины: $(x_0, y_0) = (0, 0)$.

4. Координаты некоторых точек:

• Для того чтобы построить график, найдём значения функции для нескольких точек:
  • При $x = -8$, $y = \sqrt[3]{-8} = -2$.
  • При $x = -1$, $y = \sqrt[3]{-1} = -1$.
  • При $x = 1$, $y = \sqrt[3]{1} = 1$.
  • При $x = 8$, $y = \sqrt[3]{8} = 2$.
• Таким образом, получаем следующие точки для построения графика:

  $$\begin{array}{c|c|c|c|c} x & -8 & -1 & 1 & 8 \\ \hline y & -2 & -1 & 1 & 2 \\ \end{array}$$

5. График функции:

• График функции $y = \sqrt[3]{x}$ имеет характерную форму «S». Он проходит через начало координат $(0, 0)$, и его части для положительных и отрицательных $x$ симметричны относительно начала координат. Для отрицательных значений $x$ график также уходит вниз, что отражает отрицательные значения кубического корня.
• График будет монотонно возрастать и не будет ограничен сверху или снизу.

б) $y = |\sqrt[3]{x} — 1|$

1. Рассмотрим функцию $y = \sqrt[3]{x} — 1$:

Область определения:

• Подобно предыдущему случаю, кубический корень из $x$ определён для всех действительных чисел.
• Область определения: $x \in \mathbb{R}$.

Множество значений:

• Множество значений функции $y = \sqrt[3]{x} — 1$ также будет всё действительное множество, так как кубический корень из $x$ принимает все значения $\mathbb{R}$, и при вычитании 1 результат остаётся действительным числом.
• Множество значений: $y \in \mathbb{R}$.

Координаты вершины:

• Вершина функции $y = \sqrt[3]{x} — 1$ будет в точке, где значение функции минимально. Для функции $\sqrt[3]{x} — 1$ минимальное значение возникает, когда $\sqrt[3]{x} = 1$, то есть при $x = 1$.
• При $x = 1$, $y = \sqrt[3]{1} — 1 = 0$.
• Координаты вершины: $(x_0, y_0) = (1, 0)$.

2. Построение функции $y = |\sqrt[3]{x} — 1|$:

• Мы видим, что у нас есть модуль в функции $y = |\sqrt[3]{x} — 1|$, что означает, что части графика ниже оси $x$ будут отражены относительно оси абсцисс.
• График функции $y = \sqrt[3]{x} — 1$ будет сначала как в обычной функции $\sqrt[3]{x}$, но для значений $x$ меньше 1 (где $\sqrt[3]{x} — 1$ принимает отрицательные значения), мы отразим часть графика относительно оси $x$, чтобы все значения функции стали положительными.

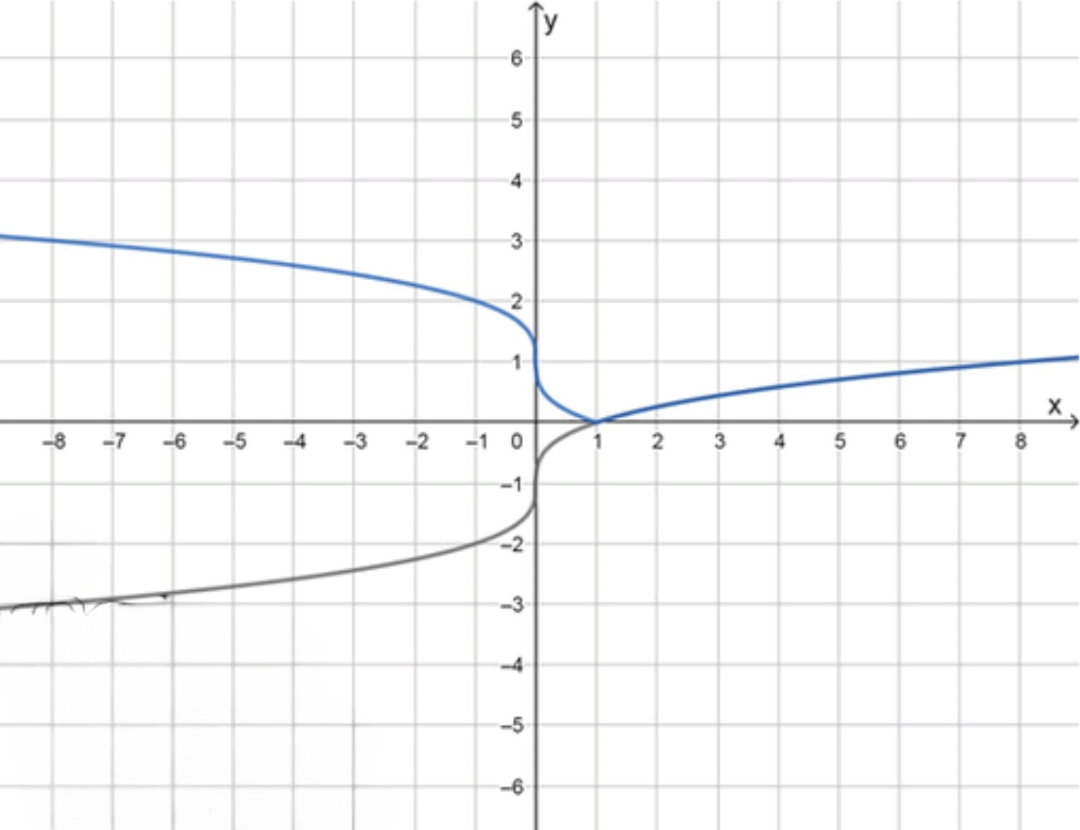
График функции:

• График функции будет иметь вершину в точке $(1, 0)$ и будет состоять из двух частей:
  • Для $x \geq 1$, функция будет такой же, как и $y = \sqrt[3]{x} — 1$, то есть возрастать.
  • Для $x < 1$, функция будет симметрична относительно оси $x$ и возрастать от нуля вверх.
• Таким образом, функция будет выглядеть как «V»-образная линия, с вершиной в точке $(1, 0)$, и вся функция будет иметь положительные значения.