ГДЗ по Алгебре 10 Класс Номер 7.20 Профильный Уровень Мордкович — Подробные Ответы

а) Воспользовавшись тем, что

$$\frac{x-5}{2x+2} = \frac{1}{2} \cdot \frac{(x+1)-6}{x+1} = \frac{1}{2} \left( 1 — \frac{6}{x+1} \right) = \frac{-3}{x+1} + \frac{1}{2},$$

постройте график функции $y = \frac{x-5}{2x+2}$. Напишите уравнения асимптот полученной гиперболы.

б) Функцию $y = \frac{ax+b}{cx+d}$, где $c \neq 0$, $\frac{a}{c} \neq \frac{b}{d}$, называют дробно-линейной функцией. Докажите, что графиком дробно-линейной функции является гипербола с асимптотами $x = -\frac{d}{c}$, $y = \frac{a}{c}$.

а) $y=\frac{x-5}{2x+2}=\frac{1}{2}\cdot \frac{(x+1)-6}{x+1}=\frac{1}{2}\cdot (1-\frac{6}{x+1})=-\frac{3}{x+1}+\frac{1}{2}$;

Область определения функции:

$$x+1\mathrm{\ne }0;$$$$x\mathrm{\ne }-1;$$

Множество значений функции:

$$y\mathrm{\ne }\frac{1}{2};$$

Уравнения асимптот гиперболы:

$$x=-1\text{и}y=\frac{1}{2};$$

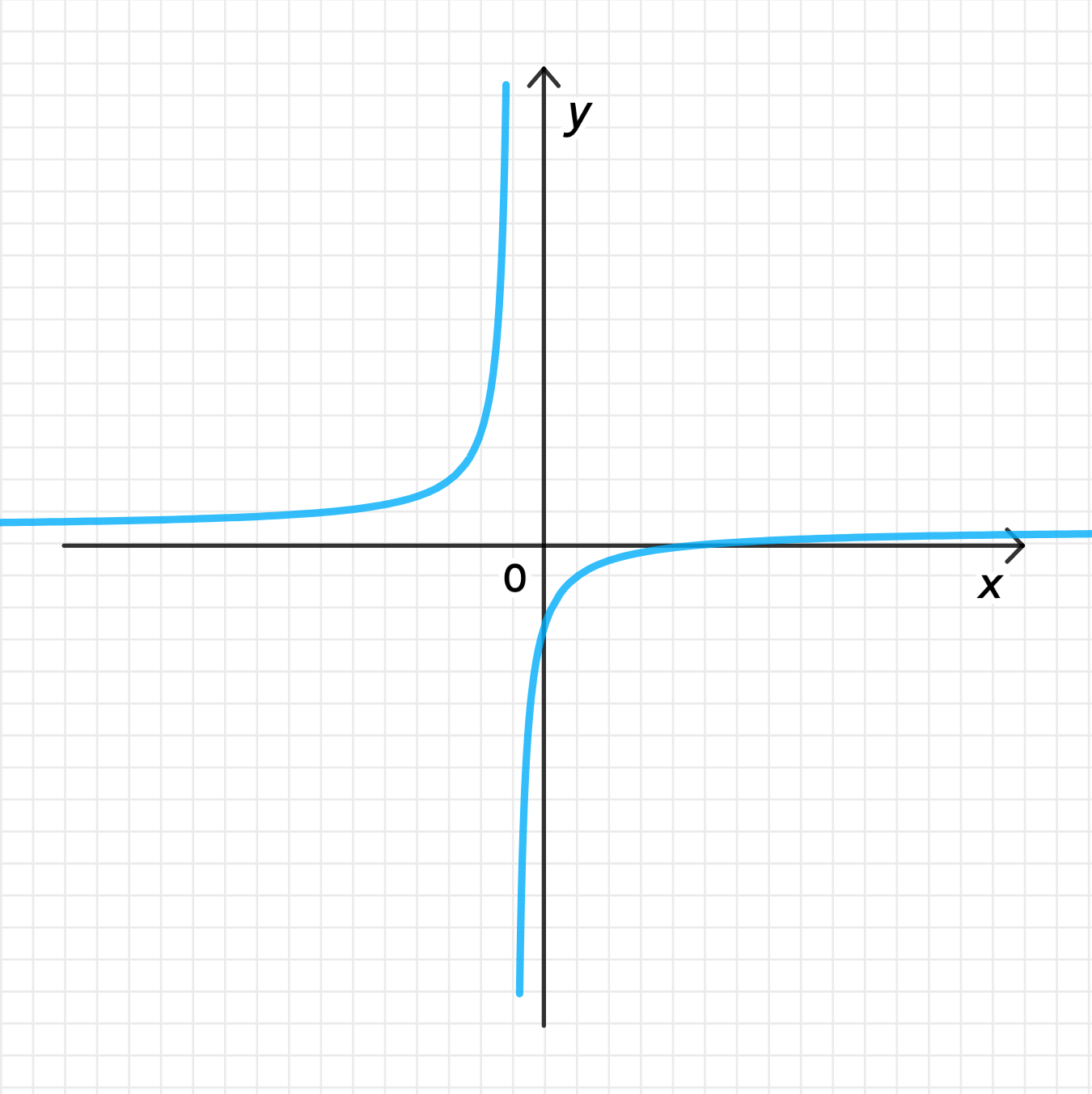
График функции:

Ответ: $x=-1;y=\frac{1}{2}$.

б) $y=\frac{ax+b}{cx+d}$, где $c\mathrm{\ne }0$ и $\frac{a}{c}\mathrm{\ne }\frac{b}{d}$;

Выразим значение $x$:

$$yc+yd=ax+b;$$$$yc-ax=b-yd;$$$$x(yc-a)=b-yd;$$$$x=\frac{b-yd}{yc-a};$$

Множество значений $x$:

$$cx+d\mathrm{\ne }0;$$$$cx\mathrm{\ne }-d;$$$$x\mathrm{\ne }-\frac{d}{c};$$

Множество значений $y$:

$$yc-a\mathrm{\ne }0;$$$$yc\mathrm{\ne }a;$$$$y\mathrm{\ne }\frac{a}{c};$$

Таким образом, дробно-линейная функция имеет две асимптоты $x=-\frac{d}{c}$ и $y=\frac{a}{c}$, следовательно ее графиком является гипербола, что и требовалось доказать.

а) $y=\frac{x-5}{2x+2}=\frac{1}{2}\cdot \frac{(x+1)-6}{x+1}=\frac{1}{2}\cdot (1-\frac{6}{x+1})=-\frac{3}{x+1}+\frac{1}{2}$

1. Область определения функции:

• Функция $y=\frac{x-5}{2x+2}$ — это дробно-линейная функция, и область её определения определяется ограничением на знаменатель.
• Чтобы знаменатель не был равен нулю, необходимо:$$2x+2\mathrm{\ne }0\Rightarrow x\mathrm{\ne }-1.$$
• Таким образом, область определения функции:$$x\in \mathbb{R},x\mathrm{\ne }-1.$$

2. Множество значений функции:

• Множество значений дробно-линейной функции можно определить, анализируя поведение функции и её асимптоты.
• Сначала рассмотрим её поведение. При $x\to \mathrm{\infty }$ и $x\to -\mathrm{\infty }$, функция стремится к асимптотическому значению $y=\frac{1}{2}$, так как:$$\underset{x\to \mathrm{\infty }}{\lim }\frac{x-5}{2x+2}=\frac{1}{2}\mathrm{.}$$

  Однако, функция не может достигнуть этого значения, так как никогда не пересечёт горизонтальную асимптоту.

• Таким образом, множество значений функции:$$y\mathrm{\ne }\frac{1}{2}\mathrm{.}$$

3. Уравнения асимптот гиперболы:

• Для дробно-линейных функций можно найти вертикальную и горизонтальную асимптоты.
• Вертикальная асимптота возникает, когда знаменатель равен нулю, то есть при $x=-1$.
  • Уравнение вертикальной асимптоты: $x=-1$.
• Горизонтальная асимптота соответствует пределу функции при $x\to \mathrm{\infty }$, что даёт значение $\frac{1}{2}$.
  • Уравнение горизонтальной асимптоты: $y=\frac{1}{2}$.

Таким образом, у функции есть две асимптоты:

$$x=-1\text{и}y=\frac{1}{2}\mathrm{.}$$

4. График функции:

• График функции является гиперболой, которая стремится к горизонтальной асимптоте $y=\frac{1}{2}$ и вертикальной асимптоте $x=-1$.
• Функция определена для всех значений $x$, кроме $x=-1$, где у неё имеется вертикальная асимптота.
• График будет иметь две части, одну в правой и одну в левой полуплоскости, с ограничением по обеим осям.

Ответ: $x=-1;y=\frac{1}{2}$.

б) $y=\frac{ax+b}{cx+d}$, где $c\mathrm{\ne }0$ и $\frac{a}{c}\mathrm{\ne }\frac{b}{d}$

1. Выразим значение $x$:

• Для получения выражения для $x$, мы начинаем с исходной функции $y=\frac{ax+b}{cx+d}$ и решаем её относительно $x$.
  • Умножим обе стороны на $cx+d$, чтобы избавиться от знаменателя:$$y(cx+d)=ax+b\mathrm{.}$$
  • Раскроем скобки:$$ycx+yd=ax+b\mathrm{.}$$
  • Переносим все члены с $x$ в левую часть уравнения:$$yc-ax=b-yd\mathrm{.}$$
  • Вынесем $x$ за скобки:$$x(yc-a)=b-yd\mathrm{.}$$
  • Разделим обе части на $yc-a$ (предполагаем, что $yc-a\mathrm{\ne }0$):$$x=\frac{b-yd}{yc-a}\mathrm{.}$$

2. Множество значений $x$:

• Чтобы функция была определена, знаменатель $cx+d$ не должен равняться нулю. Таким образом:$$cx+d\mathrm{\ne }0.$$
• Из этого следует:$$cx\mathrm{\ne }-d\Rightarrow x\mathrm{\ne }-\frac{d}{c}\mathrm{.}$$
• Следовательно, множество значений $x$ исключает точку $x=-\frac{d}{c}$.

3. Множество значений $y$:

• Чтобы функция была определена, выражение $yc-a$ не должно быть равно нулю. Таким образом:$$yc-a\mathrm{\ne }0\Rightarrow yc\mathrm{\ne }a\Rightarrow y\mathrm{\ne }\frac{a}{c}\mathrm{.}$$
• Следовательно, множество значений $y$ исключает точку $y=\frac{a}{c}$.

4. Асимптоты дробно-линейной функции:

• Для дробно-линейной функции существуют две асимптоты:
  • Вертикальная асимптота возникает, когда знаменатель функции $cx+d$ равен нулю. Это происходит при $x=-\frac{d}{c}$.
  • Горизонтальная асимптота возникает, когда функция стремится к значению $\frac{a}{c}$, при этом $y\to \frac{a}{c}$ при $x\to \mathrm{\infty }$.
• Таким образом, дробно-линейная функция имеет две асимптоты:
  • Вертикальная: $x=-\frac{d}{c}$
  • Горизонтальная: $y=\frac{a}{c}$
• График такой функции представляет собой гиперболу, с асимптотами, которые разделяют её на четыре части.

Заключение:

1. Часть а: График функции $y=\frac{x-5}{2x+2}$ является гиперболой с вертикальной асимптотой в $x=-1$ и горизонтальной асимптотой в $y=\frac{1}{2}$.
2. Часть б: График дробно-линейной функции $y=\frac{ax+b}{cx+d}$ также является гиперболой, которая имеет вертикальную асимптоту $x=-\frac{d}{c}$ и горизонтальную асимптоту $y=\frac{a}{c}$.