Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 7.21 Профильный Уровень Мордкович — Подробные Ответы
Постройте график функции и найдите область ее значений:
а) , ;
б) , ;
в) , ;
г) , .
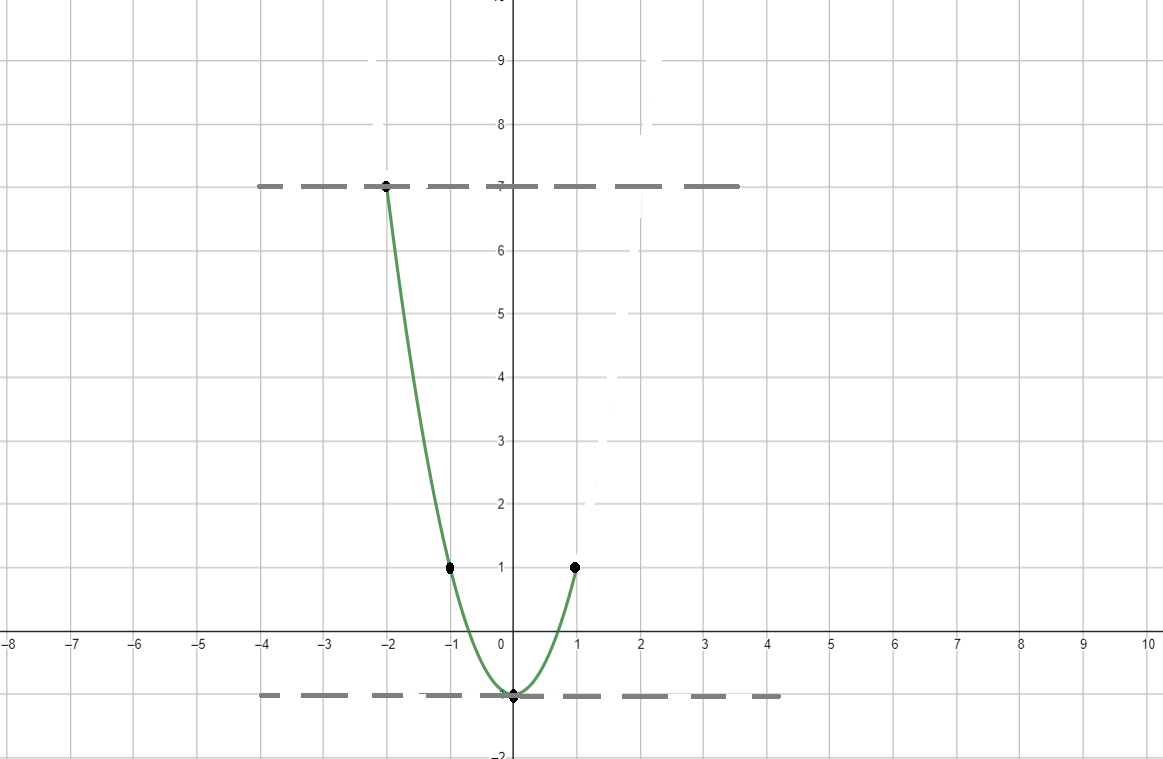
а) , где ;
Координаты вершины параболы:
Координаты некоторых точек:
График функции:
Ответ: .
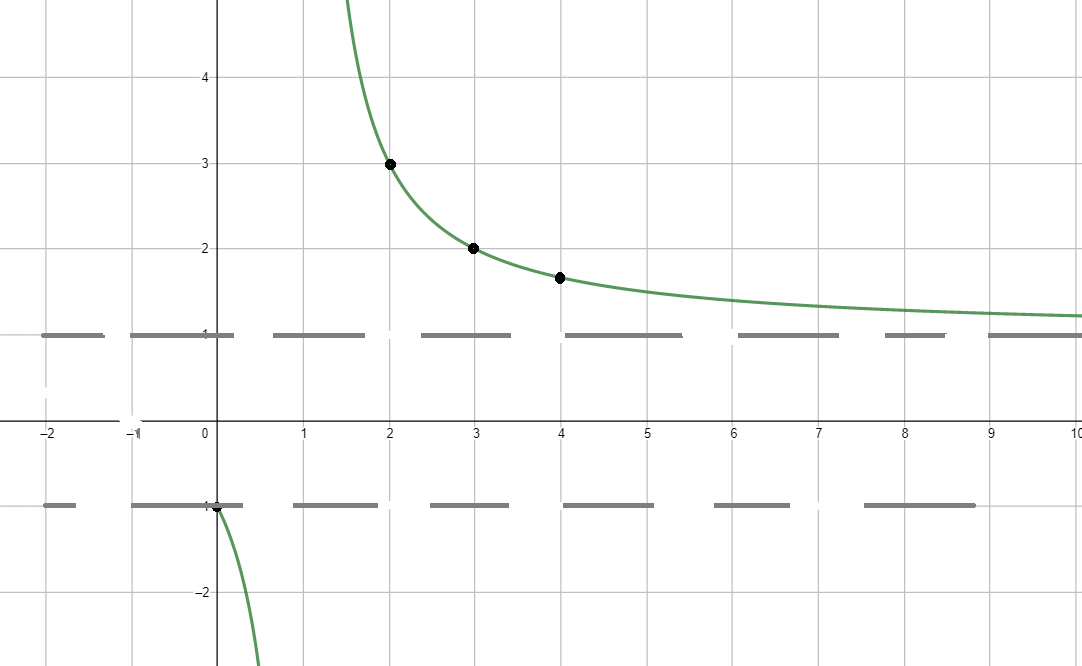
б) , где ;
Уравнения асимптот гиперболы:
Функция убывает, так как ;
Координаты некоторых точек:
График функции:
Ответ: .
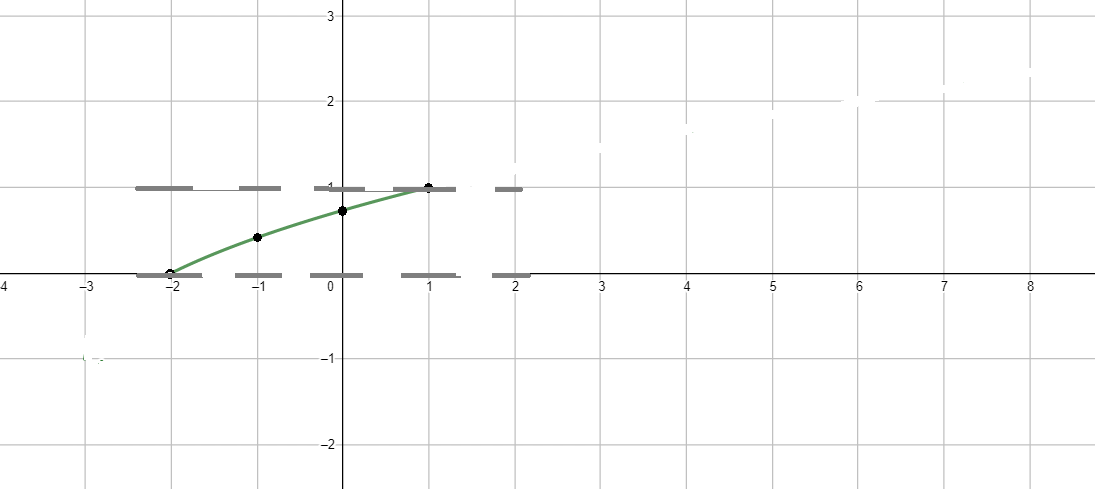
в) , где ;
Координаты вершины ветви параболы:
Координаты некоторых точек:
График функции:
Ответ: .
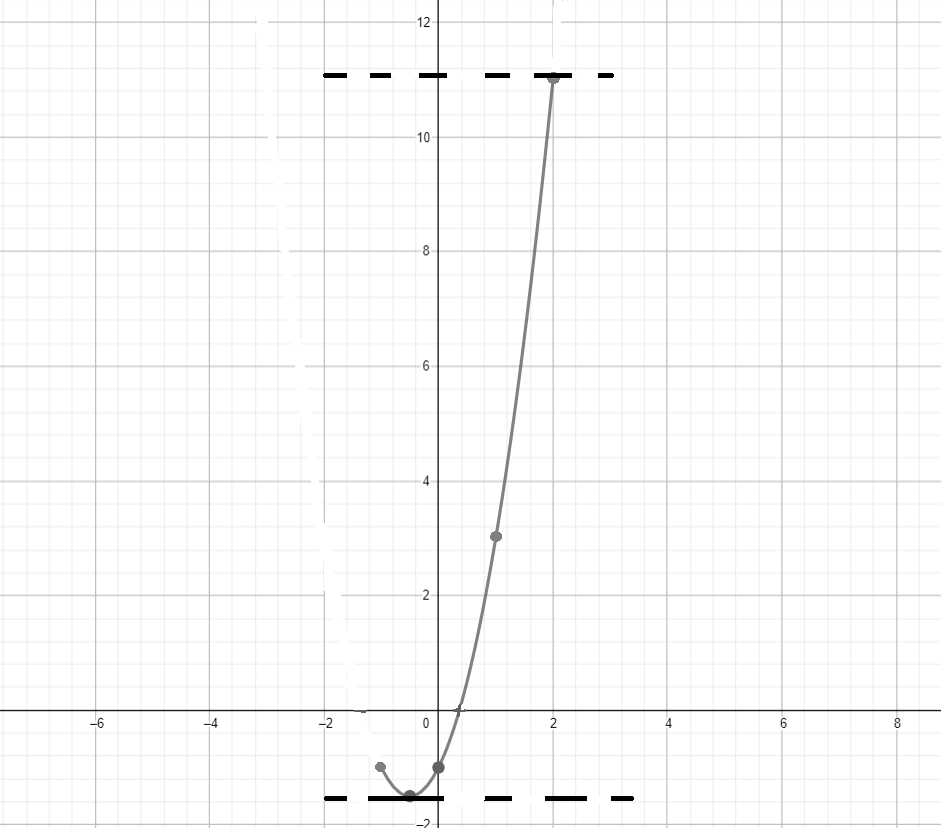
г) , где ;
Координаты вершины параболы:
Координаты некоторых точек:
График функции:
Ответ: .
а) , где
1. Координаты вершины параболы:
- Для функции , это стандартная квадратичная функция. Вершина параболы находится в точке, где производная функции равна нулю (точка экстремума). Это будет точка минимума, так как коэффициент при положительный.
Формула для нахождения абсциссы вершины параболы в функции вида дается как:
В данном случае , , , так что:
- Чтобы найти , подставим в исходную функцию:
Таким образом, координаты вершины параболы:
2. Координаты некоторых точек:
- Для того чтобы построить график, подставим несколько значений из заданного промежутка и вычислим соответствующие значения .
- При :
- При :
- При :
Таким образом, получаем следующие точки:
- При :
3. График функции:
- Функция является параболой, открывающейся вверх (так как ). Вершина параболы находится в точке , а на отрезке парабола проходит через точки , и .
- Таким образом, график будет выглядеть как парабола с вершиной в точке и симметрией относительно оси .
Ответ: .
б) , где
1. Преобразование функции:
- Мы можем преобразовать исходную функцию, чтобы удобнее было анализировать её поведение:
Это представление позволяет лучше увидеть поведение функции и её асимптоты.
2. Уравнения асимптот гиперболы:
- Вертикальная асимптота: Возникает, когда знаменатель функции равен нулю, то есть , то есть при .
- Уравнение вертикальной асимптоты: .
- Горизонтальная асимптота: Когда , дробь стремится к нулю, и функция стремится к значению . Таким образом, горизонтальная асимптота будет в .
- Уравнение горизонтальной асимптоты: .
3. Функция убывает:
- Поскольку выражение отрицательно для и положительно для , функция убывает для и возрастает для . Так как (положительное значение при преобразовании), функция имеет восходящий характер для .
4. Координаты некоторых точек:
- Подставим несколько значений из отрезка :
- При :
- При :
- При :
Таким образом, получаем следующие точки:
- При :
5. График функции:
- График функции представляет собой гиперболу с вертикальной асимптотой и горизонтальной асимптотой . Функция имеет два разделённых участка: один при , где , и второй при , где функция возрастает от значения .
Ответ: .
в) , где
1. Координаты вершины ветви параболы:
- Функция представляет собой ветвь параболы, сдвинутую на 3 единицы влево и на 1 вниз относительно стандартной функции .
- Вершина этой ветви будет при , так как когда .
Таким образом, координаты вершины: .
2. Координаты некоторых точек:
- Подставим несколько значений из отрезка :
- При :
- При :
Таким образом, получаем следующие точки:
- При :
3. График функции:
- График функции представляет собой верхнюю ветвь параболы, начиная с точки , с точками и на графике. Это сдвиг функции .
Ответ: .
г) , где
1. Координаты вершины параболы:
- Для квадратичной функции , координаты вершины можно найти по формуле для абсциссы вершины:
В данной функции , , :
- Чтобы найти ординату вершины , подставим в исходное уравнение:
Таким образом, вершина параболы имеет координаты:
2. Координаты некоторых точек:
- Подставим несколько значений из отрезка :
- При :
- При :
- При :
- При :
Получаем таблицу:
- При :
3. График функции:
- График функции — это парабола, которая открывается вверх, с вершиной в точке .
Ответ: .