ГДЗ по Алгебре 10 Класс Номер 7.22 Профильный Уровень Мордкович — Подробные Ответы

Постройте график функции $y=f(x)$ и найдите область ее определения и область ее значений:

а) $f(x)=\{\begin{array}{ll}2-x,& -3\le x\le 1;\\ x^2,& 1<x\le 2;\end{array}$

б) $f(x)=\{\begin{array}{ll}{x}^2,& -3\le x\le 1;\\ 2-x,& 1<x\le 2.\end{array}$

а) $f(x)=\{\begin{array}{ll}2-x,& \text{если }-3\le x\le 1;\\ x^2,& \text{если }1<x\le 2\end{array};$

$y=2-x$ — уравнение прямой:

$$\overline{)\begin{array}{ccc}x& -3& 1\\ y& 5& 1\end{array}}$$

$y=x^2$ — уравнение параболы:
$x_0=0$ и $y_0=0$;

$$\overline{)\begin{array}{ccc}x& 1& 2\\ y& 1& 4\end{array}}$$

Графики функций:

Ответ: $D(f)=[-3;2]$; $E(f)=[1;5]$.

б) $f(x)=\{\begin{array}{ll}{x}^2,& \text{если }-3\le x\le 1;\\ 2-x,& \text{если }1<x\le 2\end{array};$

$y=x^2$ — уравнение параболы:
$x_0=0$ и $y_0=0$;

$$\overline{)\begin{array}{ccccc}x& -3& -2& -1& 1\\ y& 9& 4& 1& 1\end{array}}$$

$y=2-x$ — уравнение прямой:

$$\overline{)\begin{array}{ccc}x& 1& 2\\ y& 1& 0\end{array}}$$

Графики функций:

Ответ: $D(f)=[-3;2]$; $E(f)=[0;9]$.

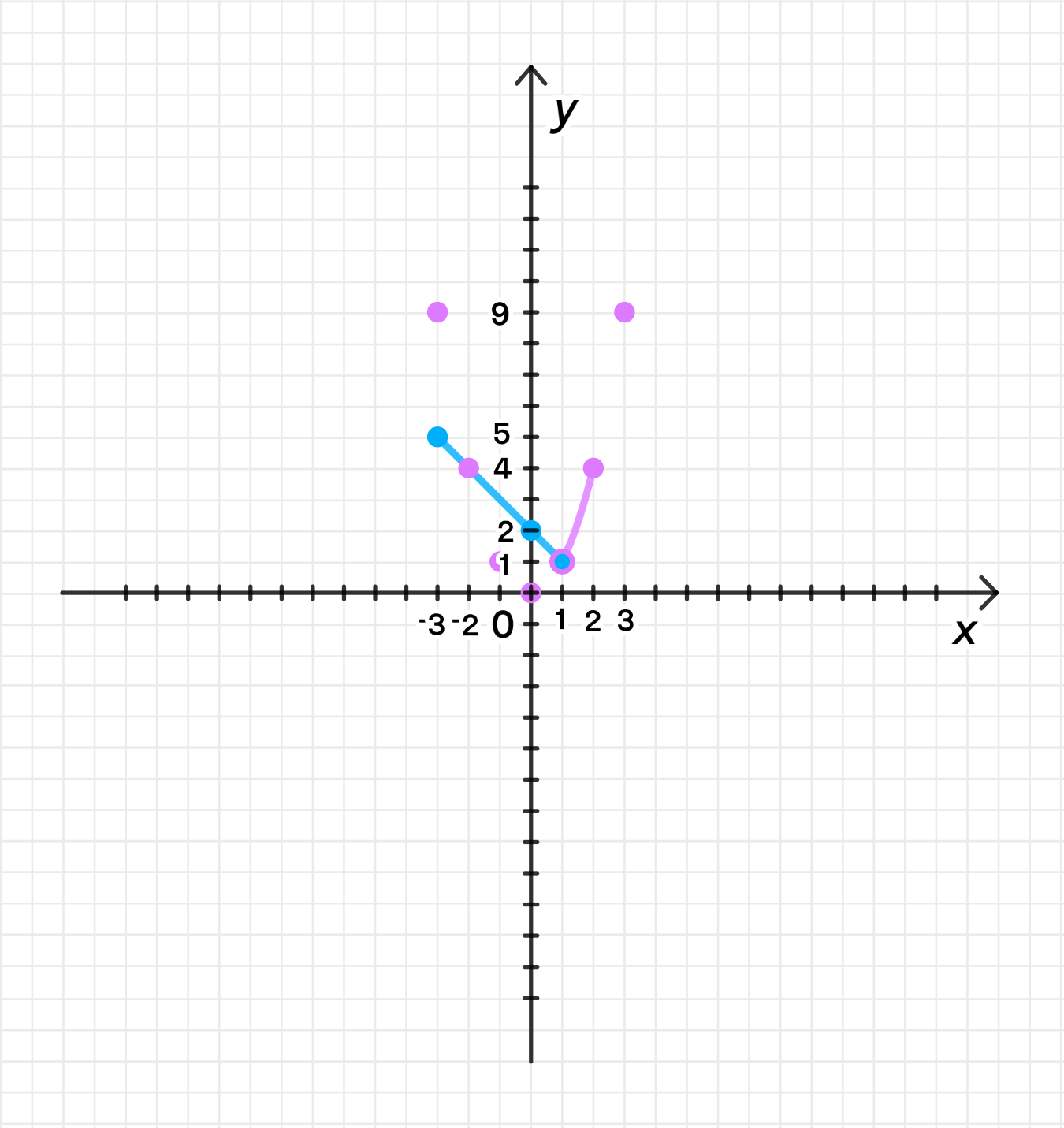
а) Функция задана кусочно:

$$f(x)=\{\begin{array}{ll}2-x,& \text{если }-3\le x\le 1;\\ x^2,& \text{если }1<x\le 2\end{array}$$

График функции $y=2-x$ на интервале $-3\le x\le 1$:

Это линейная функция с угловым коэффициентом $-1$. Проверим значения на концах интервала:

• Когда $x=-3$, $y=2-(-3)=2+3=5$.
• Когда $x=1$, $y=2-1=1$.

Таким образом, на интервале $[-3,1]$ точками на графике будут:

$$\overline{)\begin{array}{ccc}x& -3& 1\\ y& 5& 1\end{array}}$$

Эти значения подтверждают, что функция линейная и на интервале $[-3,1]$ график представляет собой прямую, соединяющую точки $(-3,5)$ и $(1,1)$.

График функции $y=x^2$ на интервале $1<x\le 2$:

Это парабола, открывающаяся вверх. Проверим значения на концах интервала:

• Когда $x=1$, $y=1^2=1$.
• Когда $x=2$, $y=2^2=4$.

Таким образом, на интервале $(1,2]$ точками на графике будут:

$$\overline{)\begin{array}{ccc}x& 1& 2\\ y& 1& 4\end{array}}$$

Эти значения подтверждают, что на интервале $(1,2]$ график функции $y=x^2$ — парабола, проходящая через точку $(1,1)$ и заканчивающаяся в точке $(2,4)$.

Графики функций:

На графике видно, что первая часть функции — это прямая на интервале $[-3,1]$, а вторая часть — парабола на интервале $(1,2]$. Обратите внимание, что функции на концах интервалов в точке $x=1$ совпадают, так как $f(1)=1$ для обеих частей.

Ответ для части (а):

• Область определения $D(f)$ — это объединение интервалов, на которых функция определена, то есть $D(f)=[-3,2]$.
• Область значений $E(f)$ — это множество всех возможных значений функции. Минимальное значение функции — $1$, а максимальное — $5$, так как на первом интервале функция достигает значения $5$, а на втором — $4$. Таким образом, $E(f)=[1,5]$.

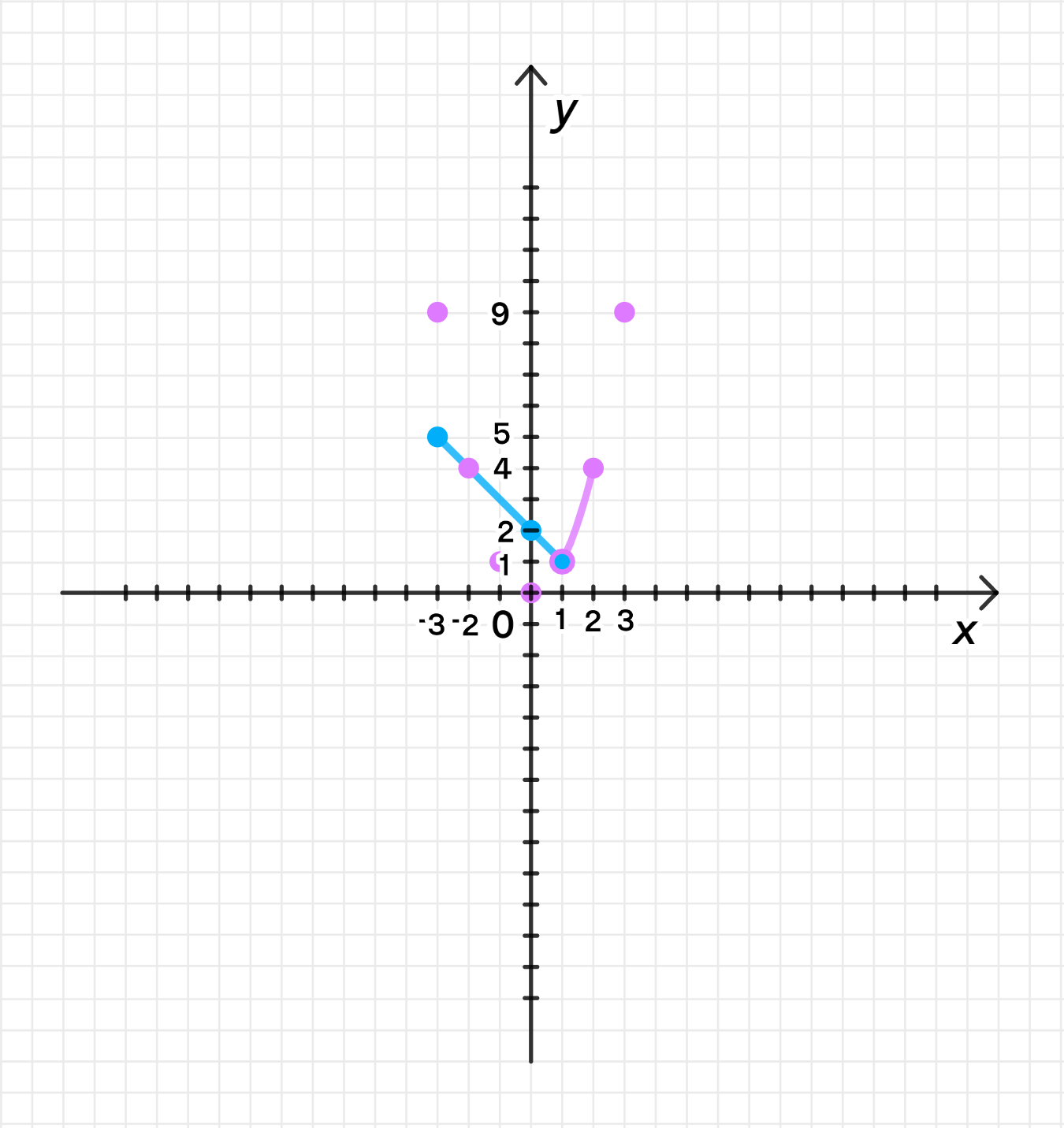
б) Функция задана кусочно:

$$f(x)=\{\begin{array}{ll}{x}^2,& \text{если }-3\le x\le 1;\\ 2-x,& \text{если }1<x\le 2\end{array}$$

График функции $y=x^2$ на интервале $-3\le x\le 1$:

Это парабола, открывающаяся вверх. Проверим значения на концах интервала:

• Когда $x=-3$, $y=(-3{)}^2=9$.
• Когда $x=-2$, $y=(-2{)}^2=4$.
• Когда $x=-1$, $y=(-1{)}^2=1$.
• Когда $x=1$, $y=1^2=1$.

Таким образом, на интервале $[-3,1]$ точками на графике будут:

$$\overline{)\begin{array}{ccccc}x& -3& -2& -1& 1\\ y& 9& 4& 1& 1\end{array}}$$

Эти значения подтверждают, что на интервале $[-3,1]$ график функции $y=x^2$ представляет собой параболу, которая проходит через точки $(-3,9)$, $(-2,4)$, $(-1,1)$, и $(1,1)$.

График функции $y=2-x$ на интервале $1<x\le 2$:

Это линейная функция с угловым коэффициентом $-1$. Проверим значения на концах интервала:

• Когда $x=1$, $y=2-1=1$.
• Когда $x=2$, $y=2-2=0$.

Таким образом, на интервале $(1,2]$ точками на графике будут:

$$\overline{)\begin{array}{ccc}x& 1& 2\\ y& 1& 0\end{array}}$$

Эти значения подтверждают, что на интервале $(1,2]$ график функции $y=2-x$ — прямая, соединяющая точки $(1,1)$ и $(2,0)$.

Графики функций:

На графике видно, что первая часть функции — это парабола на интервале $[-3,1]$, а вторая часть — прямая на интервале $(1,2]$. В точке $x=1$ обе части функции совпадают, так как $f(1)=1$.

Ответ для части (б):

• Область определения $D(f)$ — это объединение интервалов, на которых функция определена, то есть $D(f)=[-3,2]$.
• Область значений $E(f)$ — это множество всех возможных значений функции. Минимальное значение функции — $0$, а максимальное — $9$, так как на первом интервале функция достигает значения $9$, а на втором — $1$. Таким образом, $E(f)=[0,9]$.

Итоговые ответы:

а)

• $D(f)=[-3;2]$
• $E(f)=[1;5]$

б)

• $D(f)=[-3;2]$
• $E(f)=[0;9]$