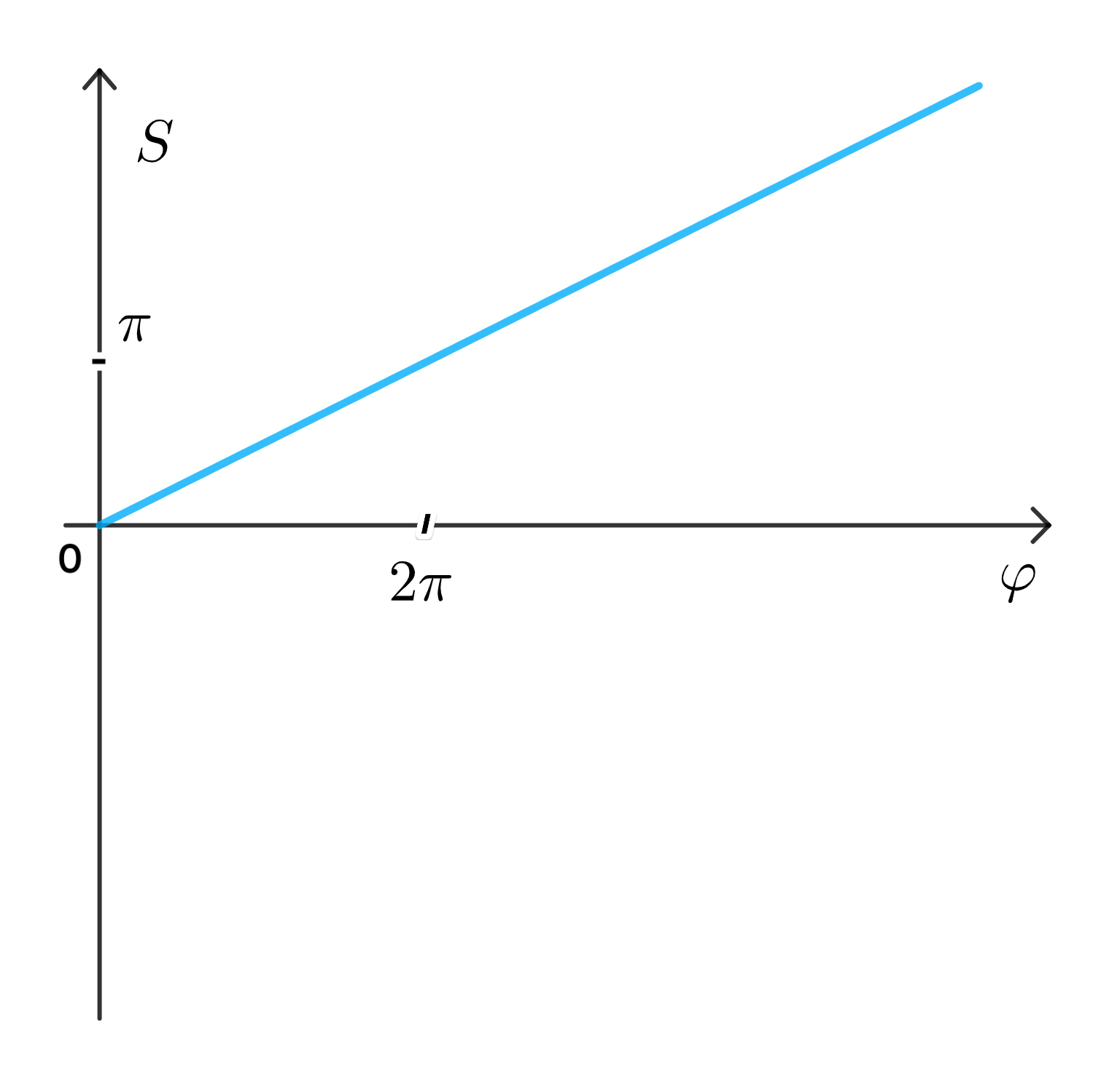ГДЗ по Алгебре 10 Класс Номер 7.4 Профильный Уровень Мордкович — Подробные Ответы

На рисунке 6 изображен сектор круга, радиус которого равен 1, а центральный угол равен $\varphi$, причем $\varphi \in (0; 2\pi)$.

а) Выразите площадь $S$ этого сектора как функцию угла $\varphi$:

$$S = S(\varphi).$$

Постройте график функции $S = S(\varphi)$.

б) Вычислите значение функции $S = S(\varphi)$ при $\varphi = \frac{\pi}{3}$.

в) Найдите $S(2) — S(1)$.

г) Найдите $S(\varphi + \delta) — S(\varphi)$.

На рисунке 2 изображен сектор круга, радиус которого равен 1, а центральный угол равен $\phi$, причем $\phi \in (0;2\pi )$;

а) Выразим площадь $S$ этого сектора как функцию угла $\phi$:
$S(\phi )=\frac{\pi R^2}{2\pi }\cdot \phi =\frac{\phi R^2}{2}=\frac{\phi \cdot 1^2}{2}=\frac{\phi }{2};$

Наименьшее значение функции:
$S(0)=\frac{0}{2}=0;$

Наибольшее значение функции:
$S(2\pi )=\frac{2\pi }{2}=\pi ;$

График функции:

б) Значение функции при $\phi =\frac{\pi }{3}$:
$S\left(\frac{\pi }{3}\right)=\frac{\pi }{3}:2=\frac{\pi }{3\cdot 2}=\frac{\pi }{6};$

в) Значение разности:
$S(2)-S(1)=\frac{2}{2}-\frac{1}{2}=\frac{1}{2};$

г) Значение разности:
$S(\phi +\delta )-S(\phi )=\frac{\phi +\delta }{2}-\frac{\phi }{2}=\frac{\delta }{2}$

На рисунке 2 изображен сектор круга, радиус которого равен 1, а центральный угол равен $\phi$, причем $\phi \in (0;2\pi )$.

а) Выражение площади сектора $S$ как функции угла $\phi$:

Сектор круга — это часть круга, ограниченная двумя радиусами и дугой, на которую эти радиусы опираются. Площадь сектора можно выразить через угол, заключенный между радиусами, и радиус круга.

Площадь круга с радиусом $R$ вычисляется по формуле:

$$S_{\text{круга}}=\pi R^2\mathrm{.}$$

Так как сектор — это часть круга, то его площадь зависит от угла $\phi$, который выражается как доля полного угла $2\pi$. Таким образом, площадь сектора можно выразить как долю площади круга, пропорциональную углу $\phi$.

Площадь сектора, ограниченного углом $\phi$, будет:

$$S(\phi )=\frac{\phi }{2\pi }\cdot \pi R^2\mathrm{.}$$

Здесь $\frac{\phi }{2\pi }$ — это доля полного угла, и, соответственно, $\frac{\phi }{2\pi }\cdot \pi R^2$ — это соответствующая доля площади круга.

Подставляем $R=1$ (радиус равен 1):

$$S(\phi )=\frac{\phi }{2\pi }\cdot \pi \cdot 1^2=\frac{\phi }{2}\mathrm{.}$$

Итак, площадь сектора как функция угла $\phi$:

$$S(\phi )=\frac{\phi }{2}\mathrm{.}$$

Наименьшее значение функции (при $\phi =0$):
Когда угол $\phi =0$, сектор сводится к точке, и его площадь будет равна нулю:

$$S(0)=\frac{0}{2}=0.$$

Наибольшее значение функции (при $\phi =2\pi$):
Когда угол $\phi =2\pi$, сектор становится полным кругом. Площадь этого круга равна $\pi$, так как радиус $R=1$:

$$S(2\pi )=\frac{2\pi }{2}=\pi \mathrm{.}$$

График функции $S(\phi )$:
График функции $S(\phi )=\frac{\phi }{2}$ будет прямой, начинающейся в точке $(0,0)$ и растущей с угловым коэффициентом $\frac{1}{2}$, пока не достигнет значения $\pi$ при $\phi =2\pi$.

б) Значение функции при $\phi =\frac{\pi }{3}$:

Чтобы найти значение функции при $\phi =\frac{\pi }{3}$, подставим этот угол в выражение для площади:

$$S\left(\frac{\pi }{3}\right)=\frac{\frac{\pi }{3}}{2}=\frac{\pi }{6}\mathrm{.}$$

Таким образом, площадь сектора при угле $\phi =\frac{\pi }{3}$ равна $\frac{\pi }{6}$.

в) Значение разности площадей для $\phi =2$ и $\phi =1$:

Чтобы найти разницу площадей, вычислим значения функции $S(\phi )$ для углов $\phi =2$ и $\phi =1$.

Для $\phi =2$:

$$S(2)=\frac{2}{2}=1.$$

Для $\phi =1$:

$$S(1)=\frac{1}{2}=\mathrm{0.5.}$$

Теперь находим разницу:

$$S(2)-S(1)=1-0.5=\mathrm{0.5.}$$

г) Значение разности площадей для углов $\phi$ и $\phi +\delta$:

Предположим, что угол увеличивается на небольшую величину $\delta$. Нужно найти разницу площадей для углов $\phi$ и $\phi +\delta$.

Площадь сектора при угле $\phi +\delta$ выражается как:

$$S(\phi +\delta )=\frac{\phi +\delta }{2}\mathrm{.}$$

Площадь сектора при угле $\phi$ уже известна:

$$S(\phi )=\frac{\phi }{2}\mathrm{.}$$

Теперь находим разницу между этими площадями:

$$S(\phi +\delta )-S(\phi )=\frac{\phi +\delta }{2}-\frac{\phi }{2}=\frac{\delta }{2}\mathrm{.}$$

Эта разница показывает, что изменение площади сектора пропорционально изменению угла $\delta$ и составляет $\frac{\delta }{2}$.

Таким образом, для маленьких изменений угла разница площадей будет зависеть линейно от величины этого изменения.