Задачник «Алгебра. 10 класс» под авторством А.Г. Мордковича — это один из самых популярных учебных материалов для старшеклассников, изучающих алгебру на профильном уровне. Книга давно зарекомендовала себя как надежный помощник в подготовке к экзаменам и олимпиадам, а также в углубленном изучении математики.
ГДЗ по Алгебре 10 Класс Номер 7.61 Профильный Уровень Мордкович — Подробные Ответы
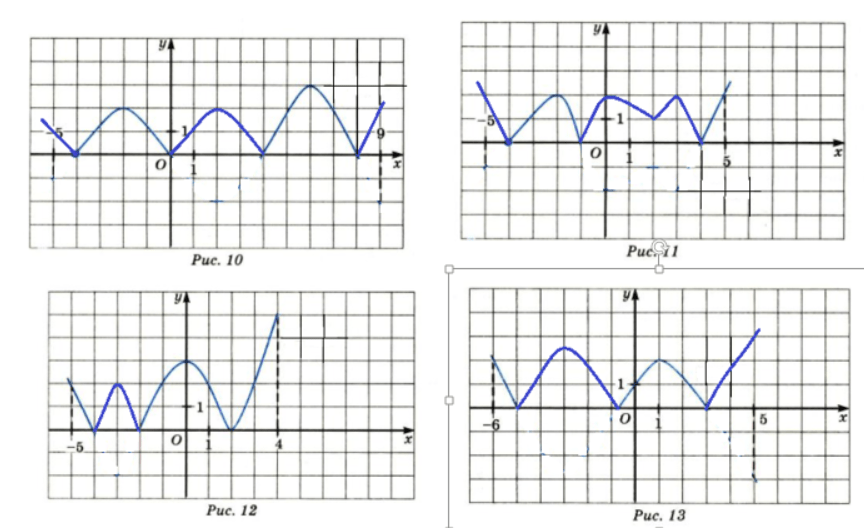
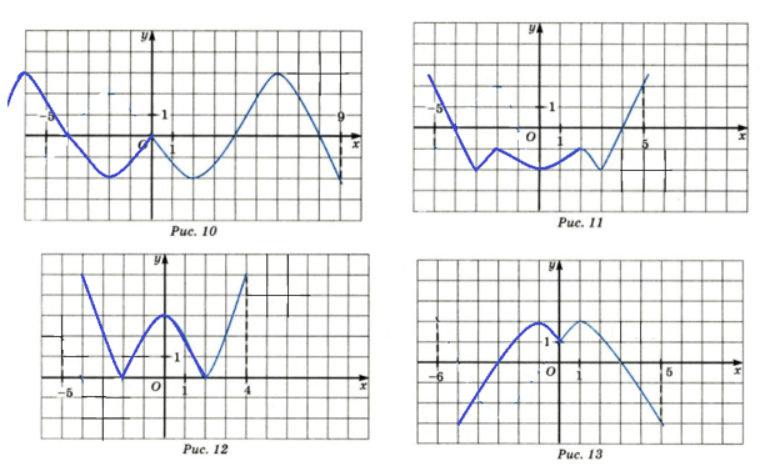
Изобразите график функции:
Рисунок 10;
а)
б)
в)
г)
Рисунок 11;
а)
б)
в)
г)
Рисунок 12;
а)
б)
в)
г)
Рисунок 13;
а)
б)
в)
г)
| Рисунок 10; а) | Рисунок 11; а) |
| Рисунок 12; а) | Рисунок 13; а) |
| Рисунок 10; б) | Рисунок 11; |
| Рисунок 12; б) | Рисунок 13; б) |
| Рисунок 10; | Рисунок 11; |
| Рисунок 12; в) | Рисунок 13; в) |
| Рисунок 10; | Рисунок 11; |
| Рисунок 13; г) |
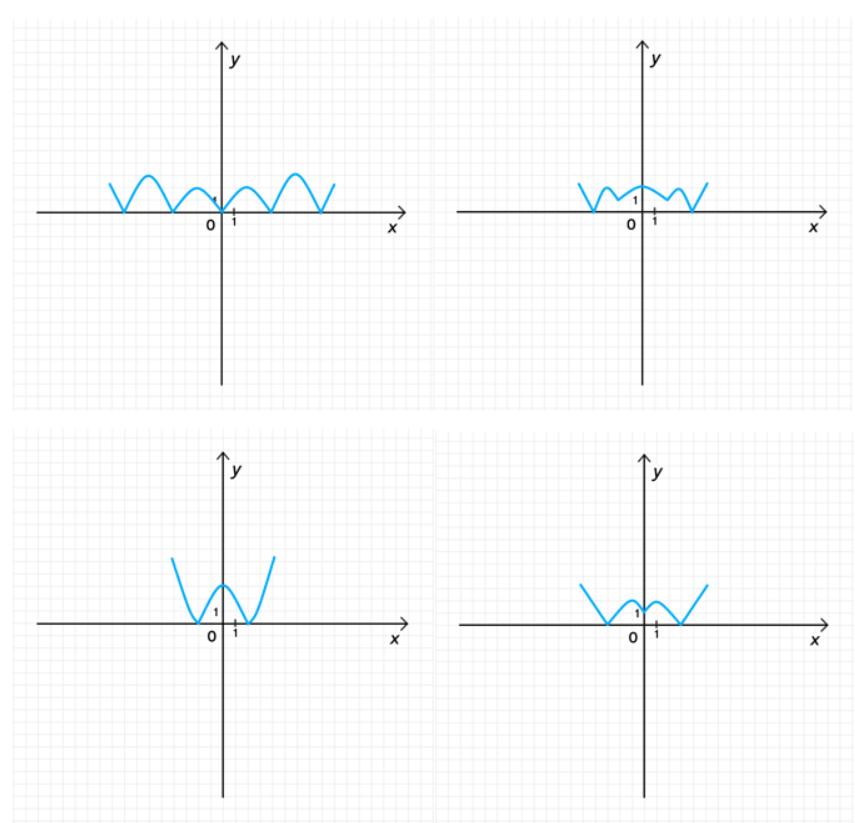
1) Рисунок 10:
а)
Давайте рассмотрим, что происходит при применении операции
Определение: Операция
Графическое представление:
- При этом график функции отрезается по оси
x x x x - Это приведет к тому, что график
y = ∣ f ( x ) ∣ y = |f(x)| f ( x ) f(x) f ( x ) f(x) x x
б)
Здесь мы имеем функцию
Определение: Операция
Графическое представление:
- График этой функции будет симметричен относительно оси
y y x x
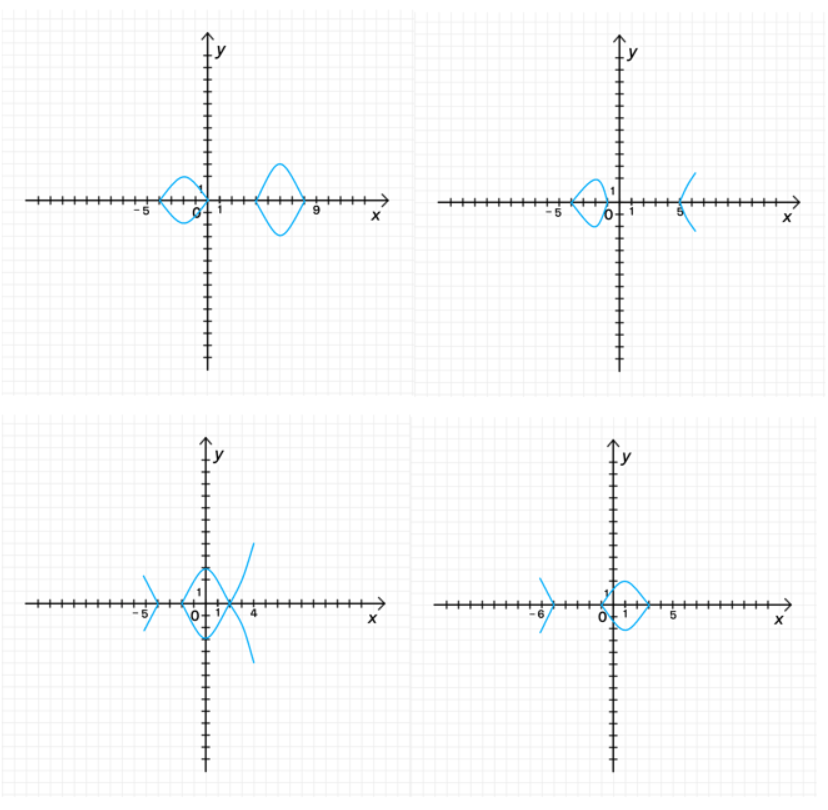
в)
Здесь мы решаем уравнение
Определение: Мы ищем такие
Графическое представление:
- График будет зеркально отражен относительно оси
x x ∣ y ∣ = f ( x ) |y| = f(x) x x y y
г)
Здесь мы решаем уравнение
Определение: Для любого
Графическое представление:
- График будет симметричен относительно вертикальной оси
y y ∣ x ∣ |x| x x y = f ( ∣ x ∣ ) y = f(|x|) y = − f ( ∣ x ∣ ) y = -f(|x|) y y
2) Рисунок 11:
- а)
y = ∣ g ( x ) ∣ y = |g(x)|
Аналогично предыдущей задаче, для функции
- б)
y = g ( ∣ x ∣ ) y = g(|x|)
Как и в предыдущем примере, эта функция будет симметрична относительно оси
- в)
∣ y ∣ = g ( x ) |y| = g(x)
Здесь мы получаем две ветви для каждого значения
- г)
∣ y ∣ = g ( ∣ x ∣ ) |y| = g(|x|)
График будет зеркален относительно оси
3) Рисунок 12:
- а)
y = ∣ h ( x ) ∣ y = |h(x)|
Для этой функции аналогичная ситуация: все отрицательные значения функции
- б)
y = h ( ∣ x ∣ ) y = h(|x|)
График этой функции будет симметричен относительно оси
- в)
∣ y ∣ = h ( x ) |y| = h(x)
График будет включать две ветви для каждого значения
- г)
∣ y ∣ = h ( ∣ x ∣ ) |y| = h(|x|)
Этот график будет симметричен относительно вертикальной оси, а для каждого значения
4) Рисунок 13:
- а)
y = ∣ φ ( x ) ∣ y = |\varphi(x)|
Все отрицательные значения функции
- б)
y = φ ( ∣ x ∣ ) y = \varphi(|x|)
График будет симметричен относительно оси
- в)
∣ y ∣ = φ ( x ) |y| = \varphi(x)
Здесь для каждого значения
- г)
∣ y ∣ = φ ( ∣ x ∣ ) |y| = \varphi(|x|)
График будет симметричен относительно оси