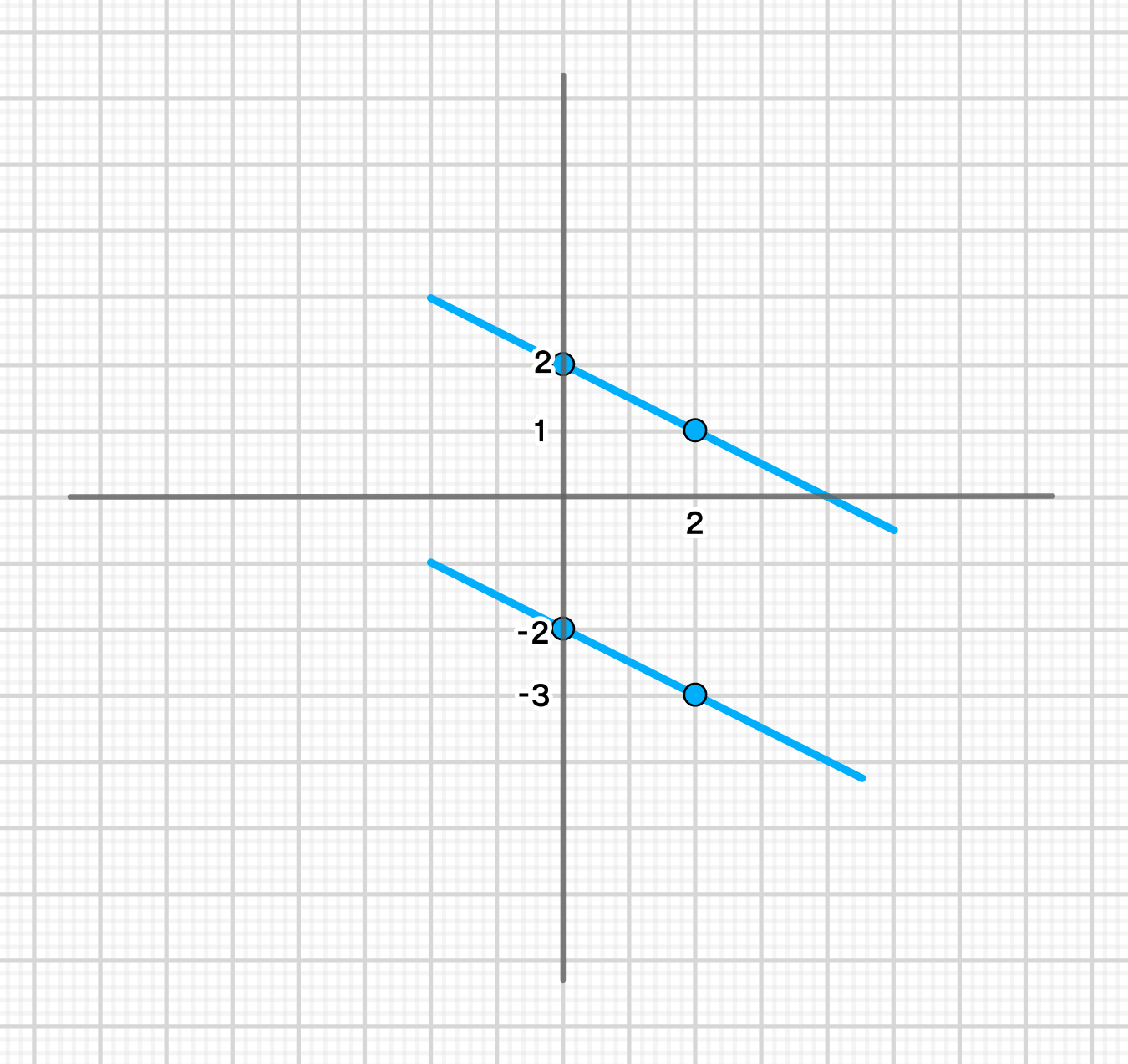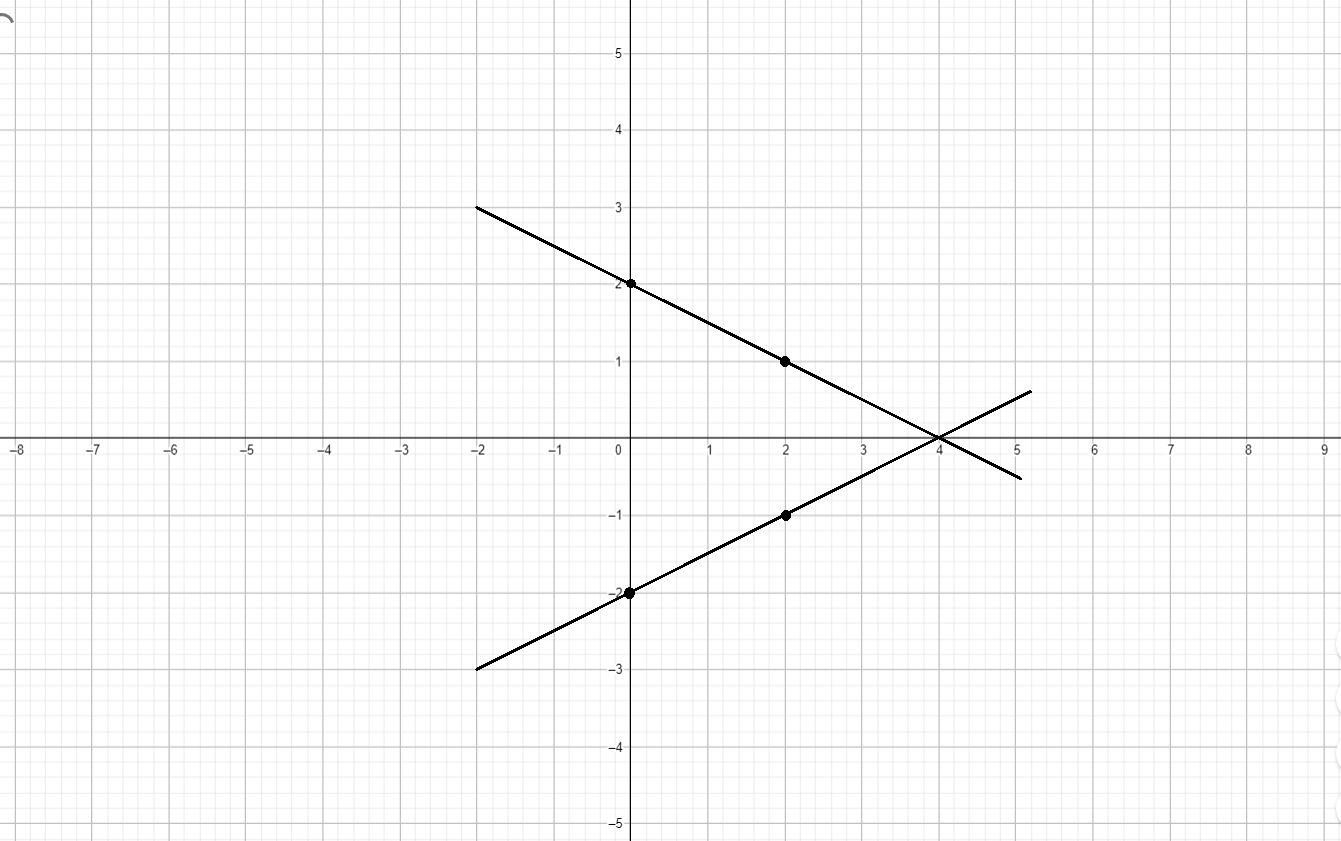ГДЗ по Алгебре 10 Класс Номер 7.62 Профильный Уровень Мордкович — Подробные Ответы

а) $|x + 2y| = 4$

Выражение под знаком модуля:

$$x + 2y \geq 0;$$ $$x \geq -2y;$$

Если $x \geq -2y$, тогда:

$$x + 2y = 4;$$ $$2y = 4 — x;$$ $$y = \frac{4 — x}{2} = 2 — \frac{x}{2};$$

Выполняется при любом $x$:

$$x \geq -2\left(2 — \frac{x}{2}\right);$$ $$x \geq -4 + x;$$ $$0x \geq -4;$$ $$x \in \mathbb{R}.$$ $$\begin{array}{|c|c|c|} \hline x & 0 & 2 \\ \hline y & 2 & 1 \\ \hline \end{array}$$

Если $x < -2y$, тогда:

$$-(x + 2y) = 4;$$ $$x + 2y = -4;$$ $$2y = -4 — x;$$ $$y = \frac{-4 — x}{2} = -2 — \frac{x}{2};$$

Выполняется при любом $x$:

$$x < -2\left(-2 — \frac{x}{2}\right);$$ $$x < 4 + x;$$ $$0x < 4;$$ $$x \in \mathbb{R}.$$ $$\begin{array}{|c|c|c|} \hline x & 0 & 2 \\ \hline y & -2 & -3 \\ \hline \end{array}$$

График уравнения:

б) $|x| + 2y = 4$

Если $x \geq 0$, тогда:

$$x + 2y = 4;$$ $$2y = 4 — x;$$ $$y = \frac{4 — x}{2} = 2 — \frac{x}{2};$$ $$\begin{array}{|c|c|c|} \hline x & 0 & 2 \\ \hline y & 2 & 1 \\ \hline \end{array}$$

Если $x < 0$, тогда:

$$-x + 2y = 4;$$ $$2y = 4 + x;$$ $$y = \frac{4 + x}{2} = 2 + \frac{x}{2};$$ $$\begin{array}{|c|c|c|} \hline x & -2 & 0 \\ \hline y & 1 & 2 \\ \hline \end{array}$$

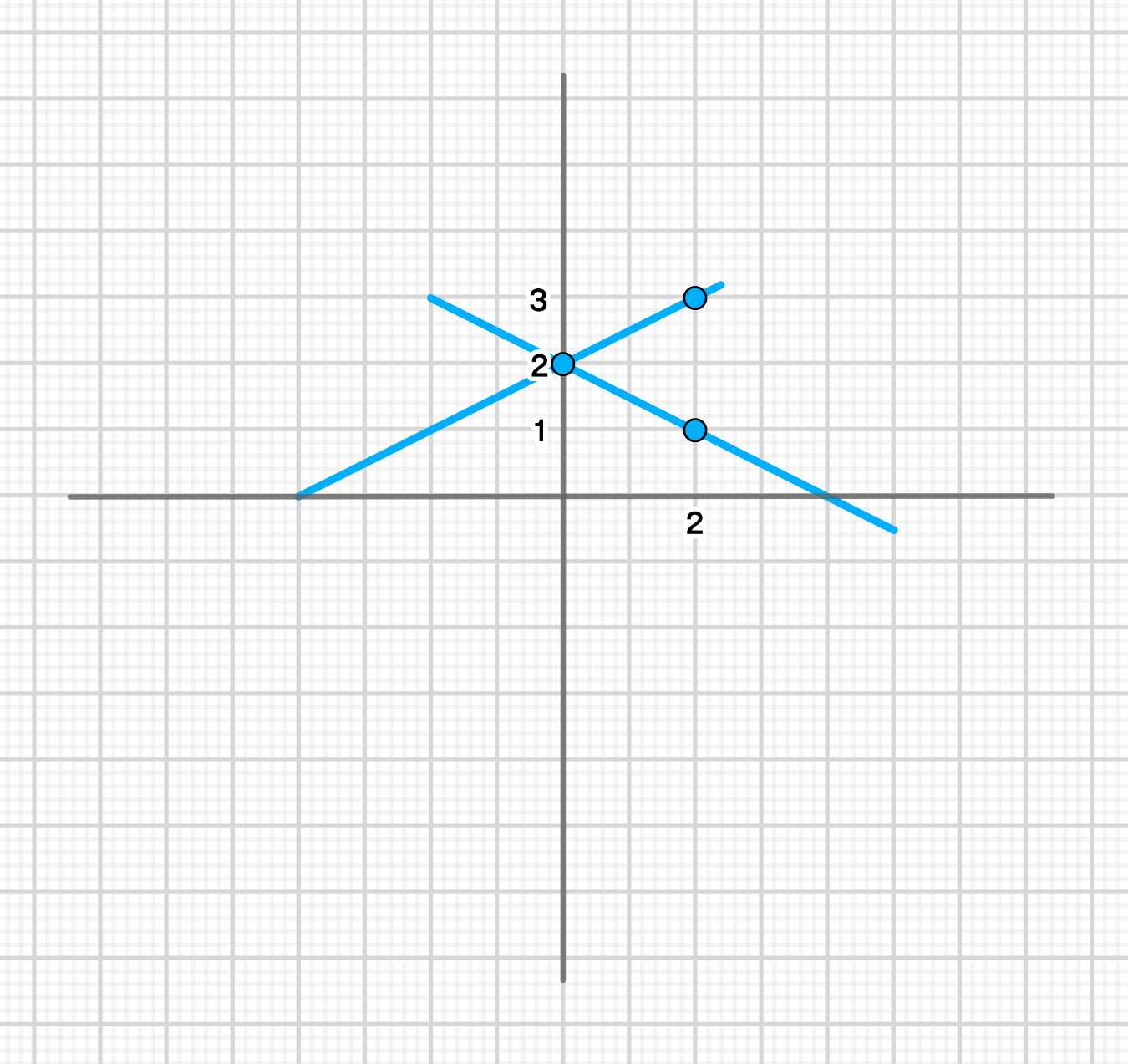
График уравнения:

в) $x + 2|y| = 4$

Если $y \geq 0$, тогда:

$$x + 2y = 4;$$ $$x = 4 — 2y;$$ $$\begin{array}{|c|c|c|} \hline y & 0 & 1 \\ \hline x & 4 & 2 \\ \hline \end{array}$$

Если $y < 0$, тогда:

$$x — 2y = 4;$$ $$x = 4 + 2y;$$ $$\begin{array}{|c|c|c|} \hline y & -1 & 0 \\ \hline x & 2 & 4 \\ \hline \end{array}$$

График уравнения:

г) $|x| + 2|y| = 4$

Если $\begin{cases} x \geq 0 \\ y \geq 0 \end{cases}$, тогда:

$$x + 2y = 4;$$ $$x = 4 — 2y;$$ $$\begin{array}{|c|c|c|} \hline y & 0 & 2 \\ \hline x & 4 & 0 \\ \hline \end{array}$$

Если $\begin{cases} x \geq 0 \\ y \leq 0 \end{cases}$, тогда:

$$x — 2y = 4;$$ $$x = 4 + 2y;$$ $$\begin{array}{|c|c|c|} \hline y & -2 & 0 \\ \hline x & 0 & 4 \\ \hline \end{array}$$

Если $\begin{cases} x \leq 0 \\ y \geq 0 \end{cases}$, тогда:

$$-x + 2y = 4;$$ $$x = 2y — 4;$$ $$\begin{array}{|c|c|c|} \hline y & 0 & 2 \\ \hline x & -4 & 0 \\ \hline \end{array}$$

Если $\begin{cases} x \leq 0 \\ y \leq 0 \end{cases}$, тогда:

$$-x — 2y = 4;$$ $$x = -2y — 4;$$ $$\begin{array}{|c|c|c|} \hline y & -2 & 0 \\ \hline x & 0 & -4 \\ \hline \end{array}$$

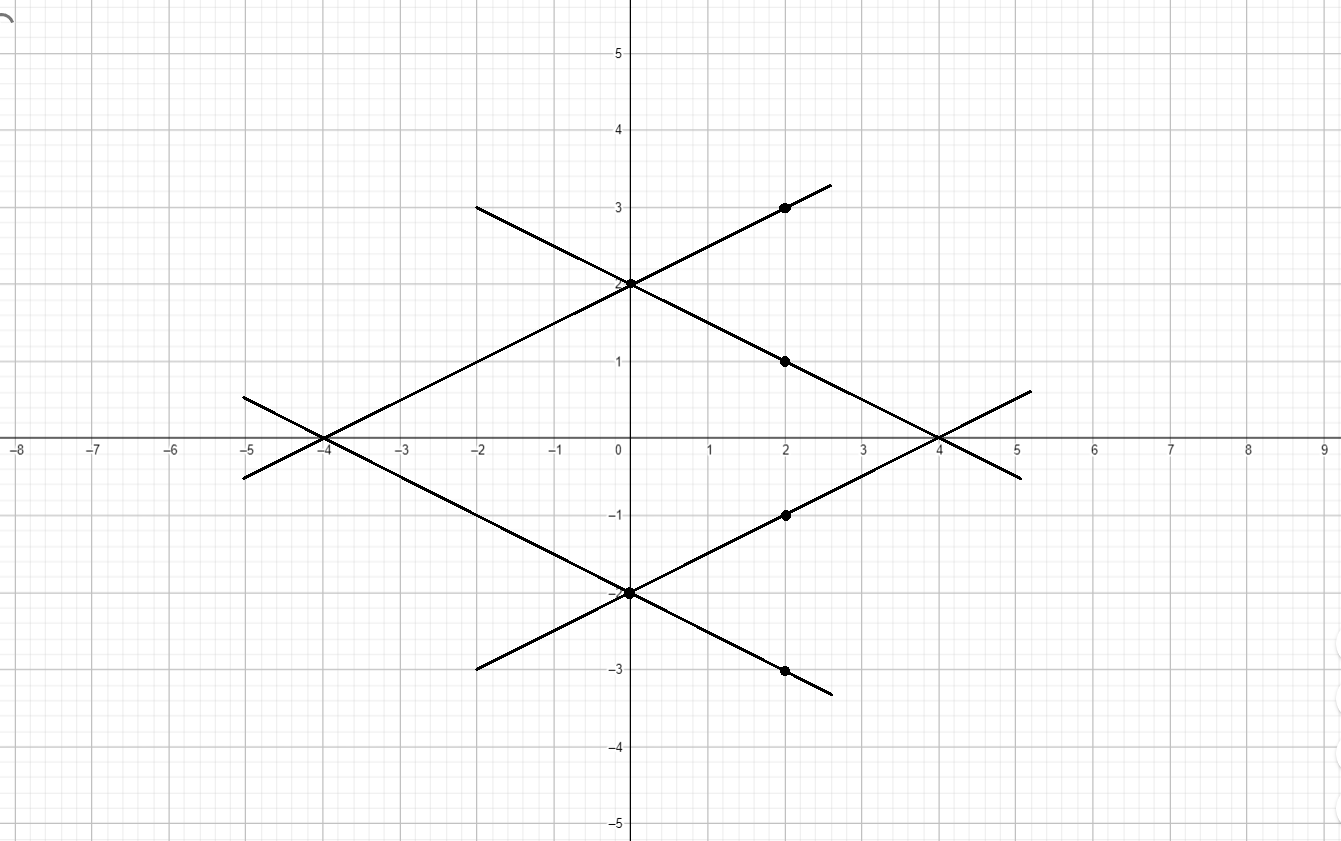
График уравнения:

а) $|x + 2y| = 4$

Для решения этого уравнения, нам нужно рассмотреть два случая, которые возникают из-за модуля.

Первый случай: $x + 2y \geq 0$

Когда $x + 2y \geq 0$, выражение под знаком модуля не меняет свой знак, и уравнение $|x + 2y| = 4$ сводится к:

$$x + 2y = 4$$

Разрешим это уравнение относительно $y$:

$$2y = 4 — x$$ $$y = \frac{4 — x}{2} = 2 — \frac{x}{2}$$

Это уравнение справедливо для всех значений $x$, удовлетворяющих условию $x + 2y \geq 0$. Подставим $y = 2 — \frac{x}{2}$ обратно в условие $x + 2y \geq 0$, чтобы проверить его выполнение:

$$x + 2\left(2 — \frac{x}{2}\right) = x + 4 — x = 4$$

Видно, что это условие выполняется для всех значений $x$. Таким образом, решение этого уравнения будет верным для всех значений $x$, то есть $x \in \mathbb{R}$.

Пример таблицы значений $x$ и $y$:

$$\begin{array}{|c|c|c|} \hline x & 0 & 2 \\ \hline y & 2 & 1 \\ \hline \end{array}$$

Второй случай: $x + 2y < 0$

В этом случае, выражение под знаком модуля меняет свой знак, и уравнение $|x + 2y| = 4$ сводится к:

$$-(x + 2y) = 4$$

Это означает:

$$x + 2y = -4$$

Разрешим это уравнение относительно $y$:

$$2y = -4 — x$$ $$y = \frac{-4 — x}{2} = -2 — \frac{x}{2}$$

Мы снова проверяем условие, при котором выполняется $x + 2y < 0$, подставив $y = -2 — \frac{x}{2}$ в это условие:

$$x + 2\left(-2 — \frac{x}{2}\right) = x — 4 — x = -4$$

Это условие выполняется для всех значений $x$. Таким образом, решение уравнения будет верным для всех значений $x$, то есть $x \in \mathbb{R}$.

Пример таблицы значений $x$ и $y$:

$$\begin{array}{|c|c|c|} \hline x & 0 & 2 \\ \hline y & -2 & -3 \\ \hline \end{array}$$

График уравнения

б) $|x| + 2y = 4$

Это уравнение также нужно рассматривать по частям, в зависимости от значения $x$.

Если $x \geq 0$

Когда $x \geq 0$, модуль $|x| = x$, и уравнение принимает вид:

$$x + 2y = 4$$

Разрешим это уравнение относительно $y$:

$$2y = 4 — x$$ $$y = \frac{4 — x}{2} = 2 — \frac{x}{2}$$

Пример таблицы значений:

$$\begin{array}{|c|c|c|} \hline x & 0 & 2 \\ \hline y & 2 & 1 \\ \hline \end{array}$$

Если $x < 0$

Когда $x < 0$, модуль $|x| = -x$, и уравнение становится:

$$-x + 2y = 4$$

Разрешим это уравнение относительно $y$:

$$2y = 4 + x$$ $$y = \frac{4 + x}{2} = 2 + \frac{x}{2}$$

Пример таблицы значений:

$$\begin{array}{|c|c|c|} \hline x & -2 & 0 \\ \hline y & 1 & 2 \\ \hline \end{array}$$

График уравнения

в) $x + 2|y| = 4$

Если $y \geq 0$

В этом случае $|y| = y$, и уравнение становится:

$$x + 2y = 4$$

Разрешим это уравнение относительно $x$:

$$x = 4 — 2y$$

Пример таблицы значений:

$$\begin{array}{|c|c|c|} \hline y & 0 & 1 \\ \hline x & 4 & 2 \\ \hline \end{array}$$

Если $y < 0$

В этом случае $|y| = -y$, и уравнение становится:

$$x — 2y = 4$$

Разрешим это уравнение относительно $x$:

$$x = 4 + 2y$$

Пример таблицы значений:

$$\begin{array}{|c|c|c|} \hline y & -1 & 0 \\ \hline x & 2 & 4 \\ \hline \end{array}$$

График уравнения

г) $|x| + 2|y| = 4$

Если $x \geq 0$ и $y \geq 0$

В этом случае $|x| = x$ и $|y| = y$, уравнение принимает вид:

$$x + 2y = 4$$

Разрешим это уравнение относительно $x$:

$$x = 4 — 2y$$

Пример таблицы значений:

$$\begin{array}{|c|c|c|} \hline y & 0 & 2 \\ \hline x & 4 & 0 \\ \hline \end{array}$$

Если $x \geq 0$ и $y \leq 0$

В этом случае $|x| = x$ и $|y| = -y$, уравнение становится:

$$x — 2y = 4$$

Разрешим это уравнение относительно $x$:

$$x = 4 + 2y$$

Пример таблицы значений:

$$\begin{array}{|c|c|c|} \hline y & -2 & 0 \\ \hline x & 0 & 4 \\ \hline \end{array}$$

Если $x \leq 0$ и $y \geq 0$

В этом случае $|x| = -x$ и $|y| = y$, уравнение становится:

$$-x + 2y = 4$$

Разрешим это уравнение относительно $x$:

$$x = 2y — 4$$

Пример таблицы значений:

$$\begin{array}{|c|c|c|} \hline y & 0 & 2 \\ \hline x & -4 & 0 \\ \hline \end{array}$$

Если $x \leq 0$ и $y \leq 0$

В этом случае $|x| = -x$ и $|y| = -y$, уравнение становится:

$$-x — 2y = 4$$

Разрешим это уравнение относительно $x$:

$$x = -2y — 4$$

Пример таблицы значений:

$$\begin{array}{|c|c|c|} \hline y & -2 & 0 \\ \hline x & 0 & -4 \\ \hline \end{array}$$

График уравнения