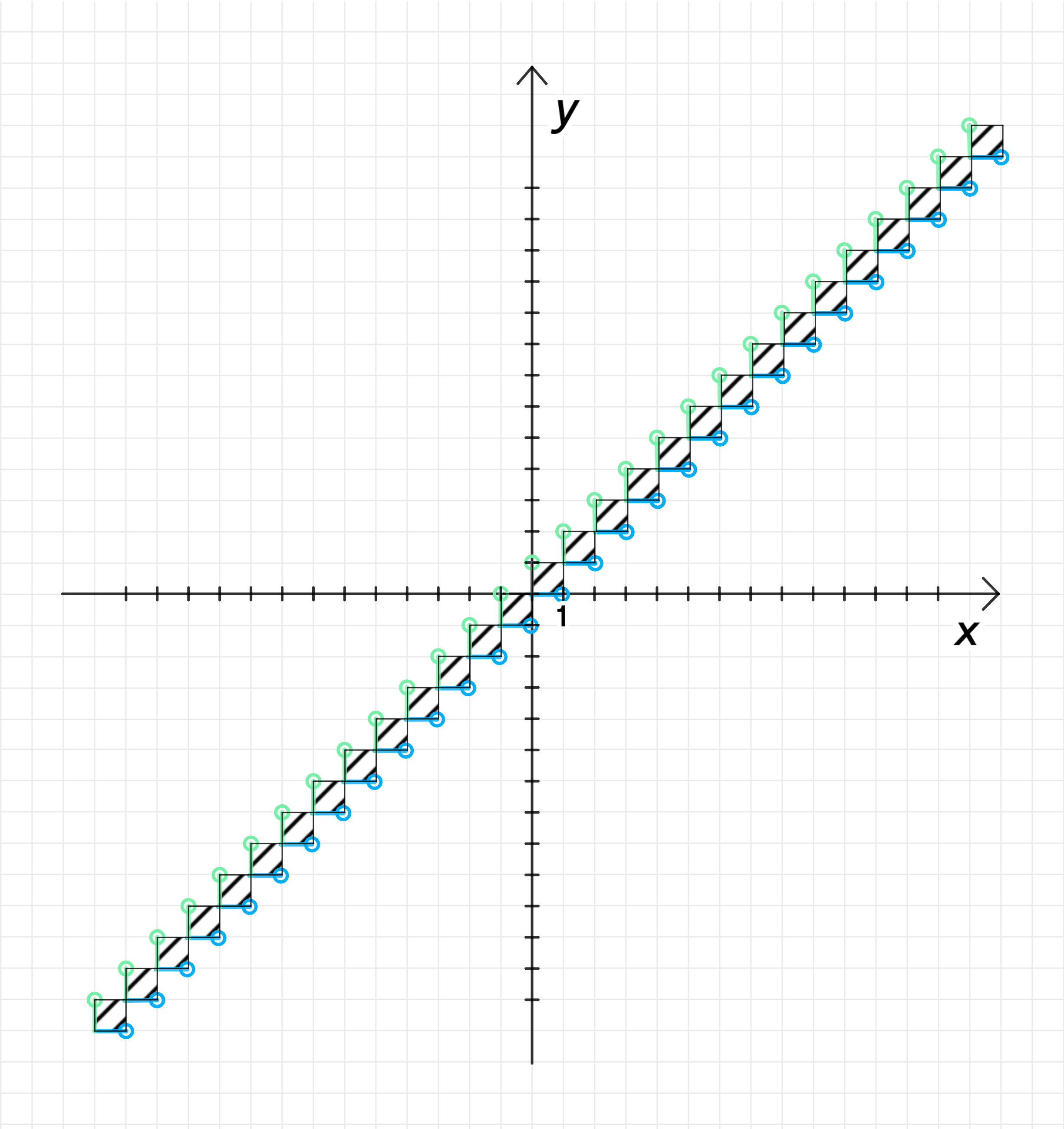ГДЗ по Алгебре 10 Класс Номер 7.68 Профильный Уровень Мордкович — Подробные Ответы

а) [x] = [y];

б) [x] > [y];

в) [x] < [y];

г) [x — 1] > [y + 1]

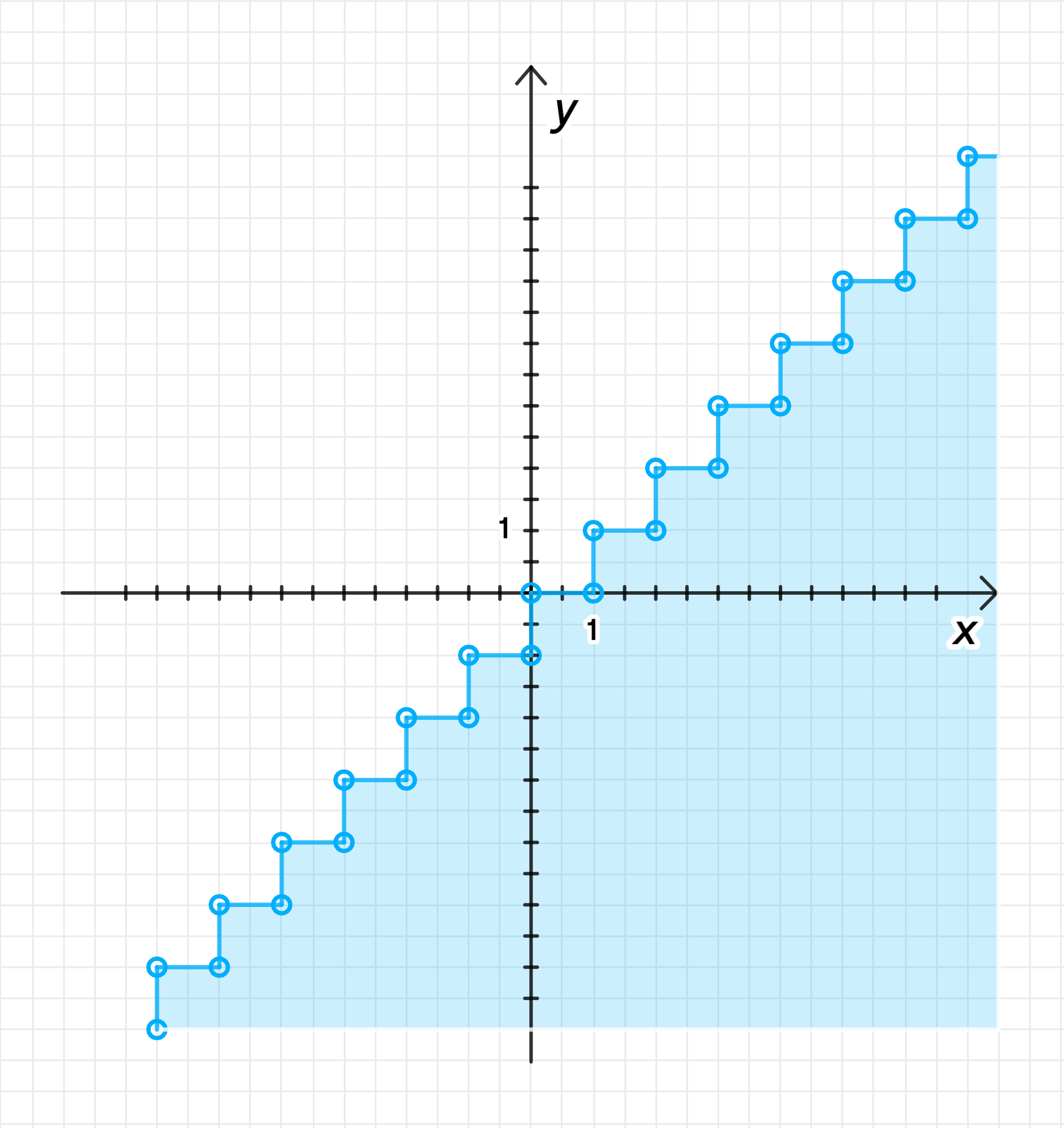
а) [x] = [y];

Первое решение:

$$[x] = [y];$$ $$x = y;$$

Второе решение:

$$[x] = [y] = k;$$ $$k \leq x < k + 1 \text{ и } k \leq y < k + 1;$$

График уравнения:

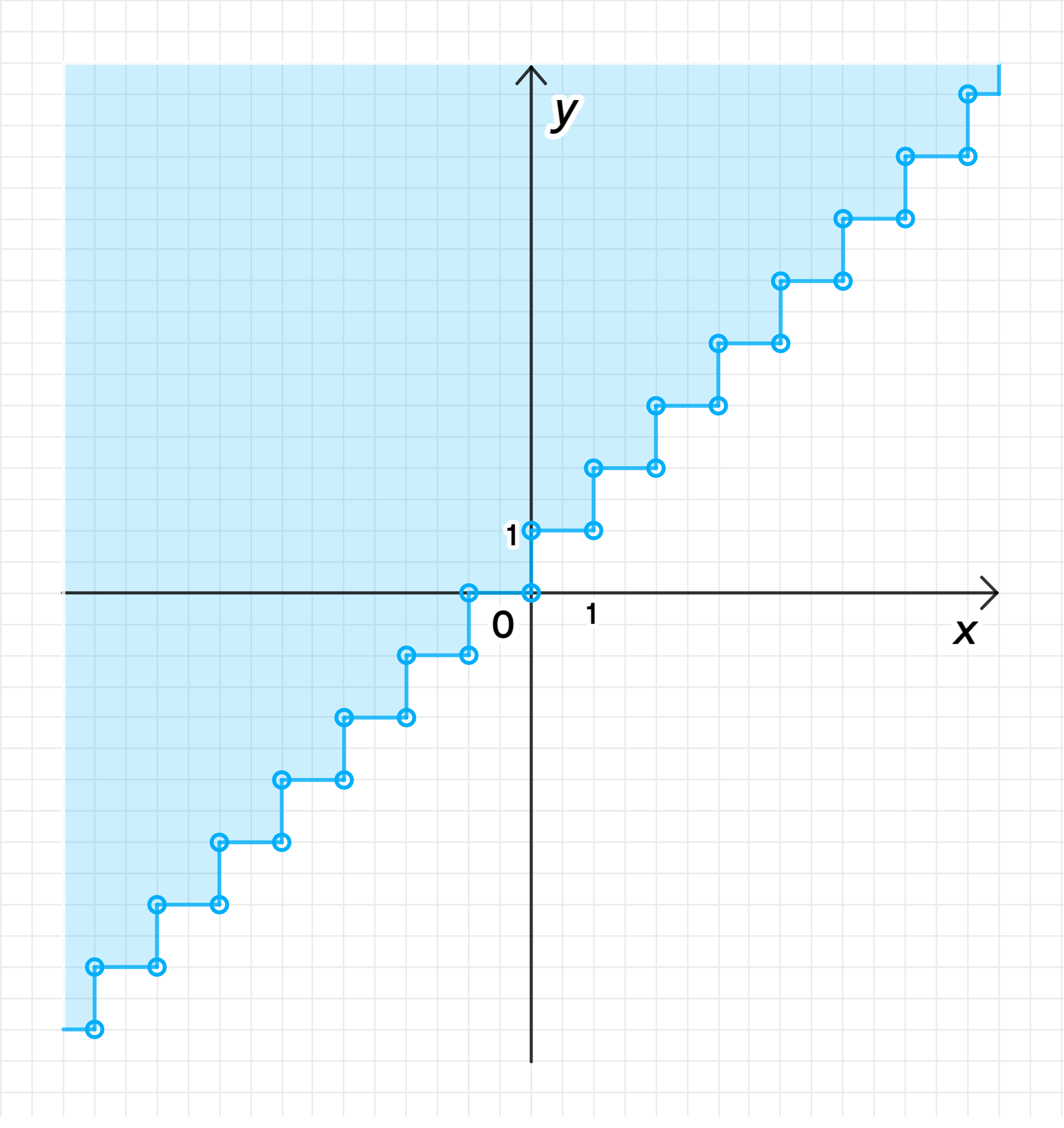
б) [x] > [y];

Решение неравенства:

$$[y] < [x] = k;$$ $$k \leq x < k + 1 \text{ и } y < k;$$

График уравнения:

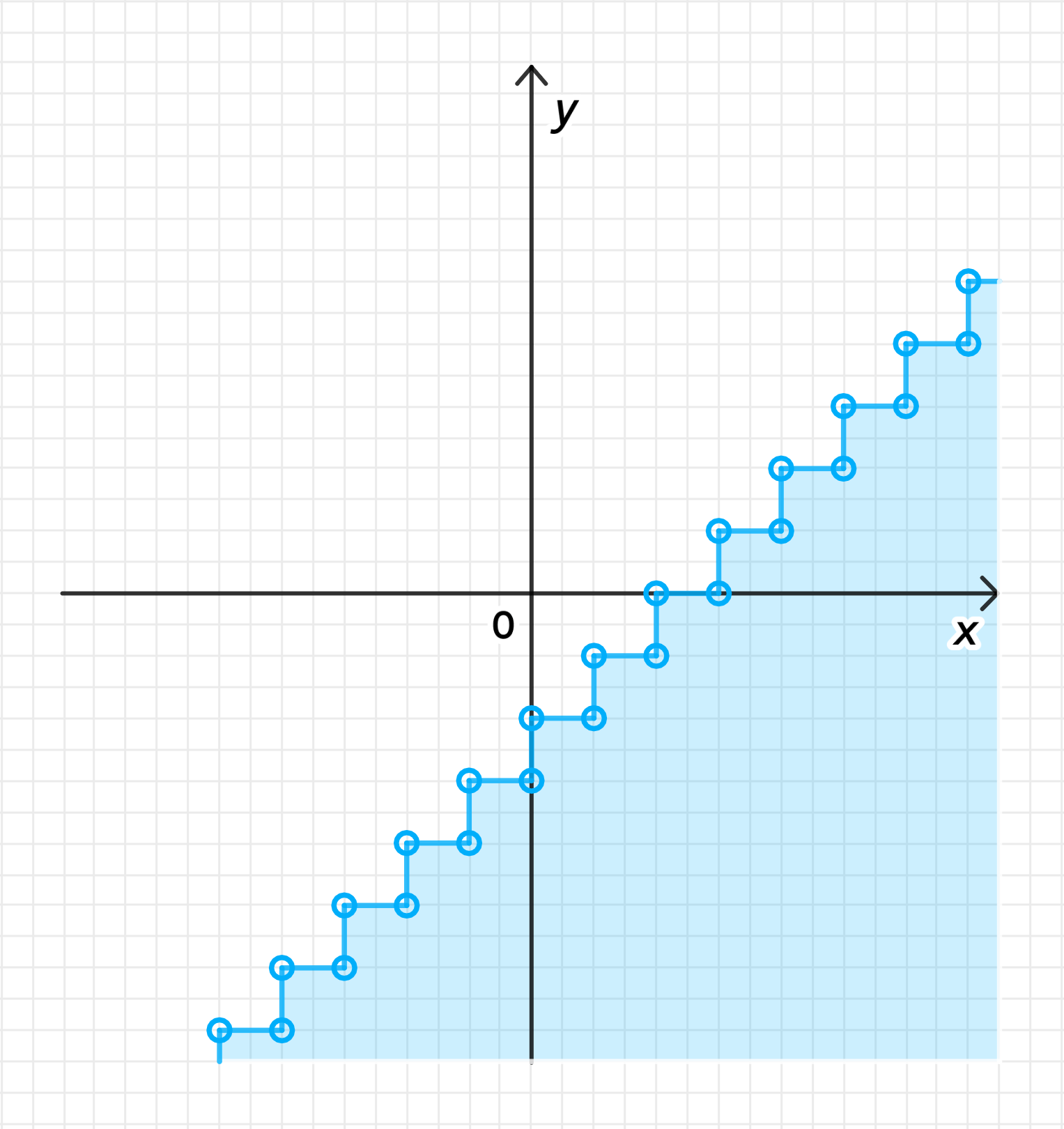
в) [x] < [y];

Решение неравенства:

$$[y] > [x] = k;$$ $$k \leq x < k + 1 \text{ и } y > k;$$

График уравнения:

г) [x — 1] > [y + 1];

Первое решение:

$$[x — 1] = [y + 1];$$ $$x — 1 = y + 1;$$ $$y = x — 2;$$

Второе решение:

$$[x — 1] = [y + 1] = k;$$ $$k \leq x — 1 < k + 1 \quad \Rightarrow \quad k + 1 \leq x < k + 2;$$ $$k \leq y + 1 < k + 1 \quad \Rightarrow \quad k — 1 \leq y < k;$$

График уравнения:

а) $[x] = [y]$

Шаг 1. Определение целой части

Целая часть числа $x$, обозначаемая $[x]$, — это наибольшее целое число, которое не превосходит $x$. Точно так же для числа $y$, $[y]$ — это наибольшее целое число, которое не превосходит $y$.

Когда $[x] = [y]$, это значит, что целая часть числа $x$ равна целой части числа $y$.

Шаг 2. Анализ первого решения

• Если $[x] = [y]$, то это означает, что числа $x$ и $y$ лежат в одном и том же интервале целых чисел. То есть их целые части одинаковы, и это может означать, что $x$ и $y$ — одинаковые числа.

Следовательно, первое возможное решение — это $x = y$. Если $x = y$, то целая часть обоих чисел будет одинаковой, и уравнение выполнится.

Шаг 3. Анализ второго решения

• Вторая возможность — это то, что $[x] = [y] = k$, где $k$ — целое число. В этом случае $x$ и $y$ могут быть любыми числами, которые принадлежат интервалу:

  $$k \leq x < k + 1 \quad \text{и} \quad k \leq y < k + 1.$$

  То есть $x$ и $y$ могут быть любыми числами, которые лежат в интервале от $k$ до $k + 1$, но сами не могут быть равны $k + 1$.

Шаг 4. График решения

б) $[x] > [y]$

Шаг 1. Понимание неравенства

Когда $[x] > [y]$, это означает, что целая часть числа $x$ больше, чем целая часть числа $y$.

Шаг 2. Решение неравенства

Если $[x] = k$, то это означает, что:

$$k \leq x < k + 1.$$

А если $[y] = m$, то это означает:

$$m \leq y < m + 1.$$

Теперь рассмотрим неравенство $[x] > [y]$, то есть $k > m$. Это означает, что целая часть $x$ больше целой части $y$. Таким образом, целая часть $x$ должна быть строго больше, чем целая часть $y$.

Если $[x] = k$, тогда $x$ лежит в интервале $[k, k+1)$, и $[y] = m$, где $y$ лежит в интервале $[m, m+1)$, причем $k > m$.

Шаг 3. Заключение

Таким образом, решение будет:

$$k \leq x < k + 1 \quad \text{и} \quad y < k.$$

То есть, $y$ должно быть меньше $k$, чтобы $[x] > [y]$.

Шаг 4. График решения

в) $[x] < [y]$

Шаг 1. Понимание неравенства

Когда $[x] < [y]$, это означает, что целая часть числа $x$ меньше, чем целая часть числа $y$.

Шаг 2. Решение неравенства

• Если $[x] = k$, то $k \leq x < k + 1$.
• Если $[y] = m$, то $m \leq y < m + 1$.

Для неравенства $[x] < [y]$, то есть $k < m$, целая часть $x$ должна быть строго меньше, чем целая часть $y$. Таким образом, $x$ лежит в интервале $[k, k + 1)$, а $y$ лежит в интервале $[m, m + 1)$, где $k < m$.

Шаг 3. Заключение

Таким образом, решение будет:

$$k \leq x < k + 1 \quad \text{и} \quad y > k.$$

Это означает, что $y$ должно быть больше, чем $k$.

Шаг 4. График решения

г) $[x — 1] > [y + 1]$

Шаг 1. Понимание неравенства

Когда $[x — 1] > [y + 1]$, это означает, что целая часть числа $x — 1$ больше, чем целая часть числа $y + 1$.

Шаг 2. Первое решение

Для начала, если $[x — 1] = [y + 1]$, то $x — 1 = y + 1$, откуда:

$$x = y + 2.$$

Шаг 3. Второе решение

Если $[x — 1] = [y + 1] = k$, то:

$$k \leq x — 1 < k + 1 \quad \Rightarrow \quad k + 1 \leq x < k + 2,$$

и

$$k \leq y + 1 < k + 1 \quad \Rightarrow \quad k — 1 \leq y < k.$$

Шаг 4. Заключение

Таким образом, $x$ будет лежать в интервале $[k+1, k+2)$, а $y$ будет лежать в интервале $[k-1, k)$.

Шаг 5. График решения

Итоговые ответы:

а) $x = y$ или $k \leq x < k + 1$ и $k \leq y < k + 1$.

б) $k \leq x < k + 1$ и $y < k$.

в) $k \leq x < k + 1$ и $y > k$.

г) $x = y + 2$ или $k + 1 \leq x < k + 2$ и $k — 1 \leq y < k$.