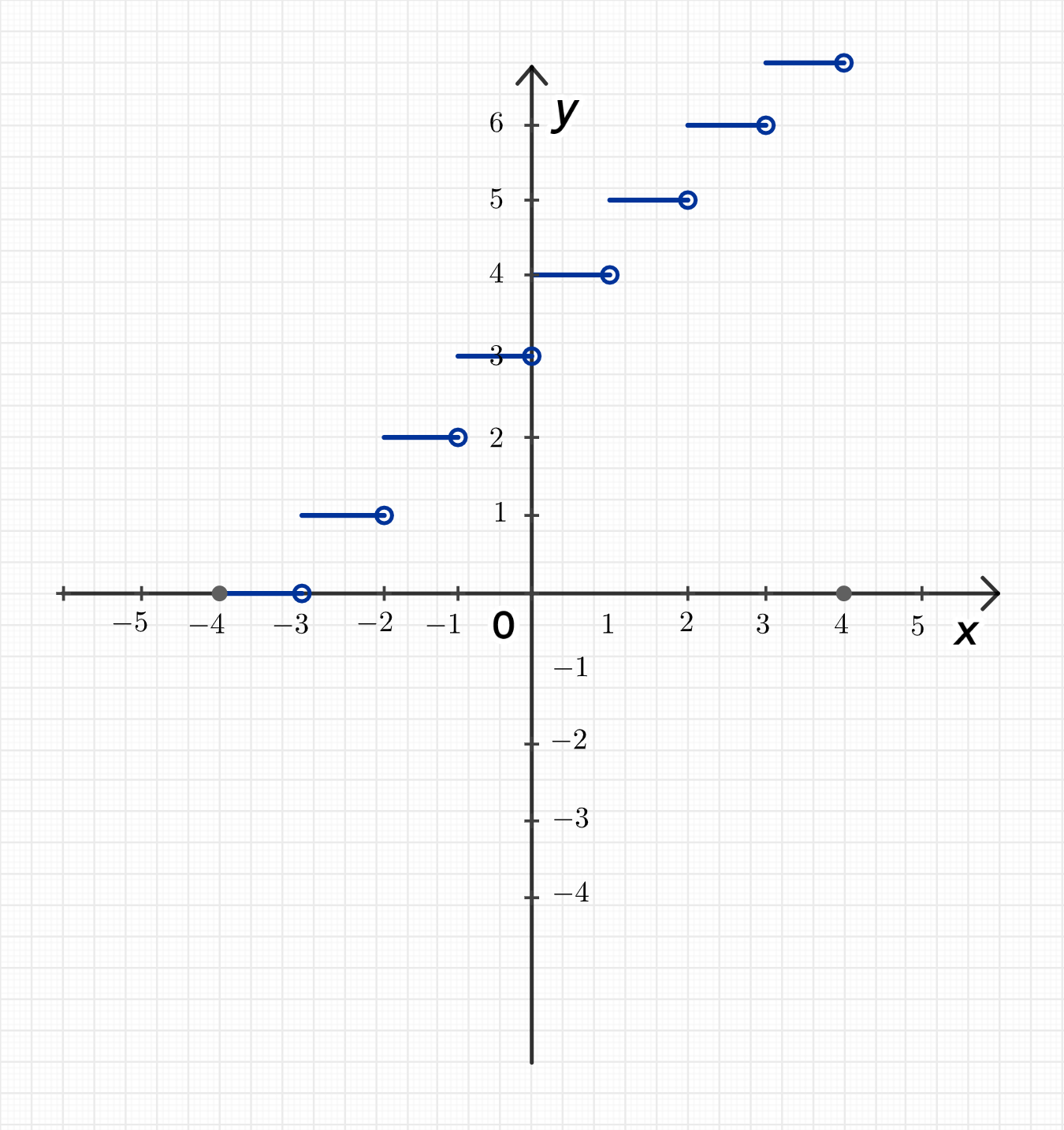ГДЗ по Алгебре 10 Класс Номер 7.73 Профильный Уровень Мордкович — Подробные Ответы

Построить график заданной функции на отрезке $[-4; 4]$:

а) $y = [x]$;

б) $y = [1 — x]$;

в) $y = [x + 4]$;

г) $y = \left[\frac{1 — x}{2}\right]$

Построить график заданной функции на отрезке $[-4; 4]$:

а) $y = [x]$;

Решение равенства:

$$y = [x] = k;$$ $$k \leq x < k + 1;$$

График функции:

б) $y = [1 — x]$;

Решение равенства:

$$y = [1 — x] = k;$$ $$k \leq 1 — x < k + 1;$$ $$k — 1 \leq -x < k;$$ $$-k < x \leq -(k — 1);$$

График функции:

в) $y = [x + 4]$;

Решение равенства:

$$y = [x + 4] = k;$$ $$k \leq x + 4 < k + 1;$$ $$k — 4 \leq x < k — 3;$$

График функции:

г) $y = \left[\frac{1 — x}{2}\right]$;

Решение равенства:

$$y = \left[\frac{1 — x}{2}\right] = k;$$ $$k \leq \frac{1 — x}{2} < k + 1;$$ $$2k \leq 1 — x < 2k + 2;$$ $$2k — 1 \leq -x < 2k + 1;$$ $$-(2k + 1) < x \leq -(2k — 1);$$

График функции:

Построить график заданной функции на отрезке $[-4; 4]$

а) $y = [x]$

Шаг 1. Определение целой части числа

Целая часть числа $x$, обозначаемая $[x]$, это наибольшее целое число, которое не превосходит $x$. Например, для $x = 2.5$, $[x] = 2$, для $x = -2.5$, $[x] = -3$.

Функция $y = [x]$ — это функция, которая на каждом интервале, между двумя целыми числами, принимает постоянное значение. Например:

• Для $x \in [0, 1)$ $y = 0$,
• Для $x \in [1, 2)$ $y = 1$,
• Для $x \in [2, 3)$ $y = 2$,
  и так далее.

Шаг 2. Решение для $y = [x]$

Решение для $y = [x]$ выглядит следующим образом:

$$y = [x] = k,$$

где $k$ — целое число, которое ограничивает интервал. То есть:

$$k \leq x < k + 1.$$

Шаг 3. График функции

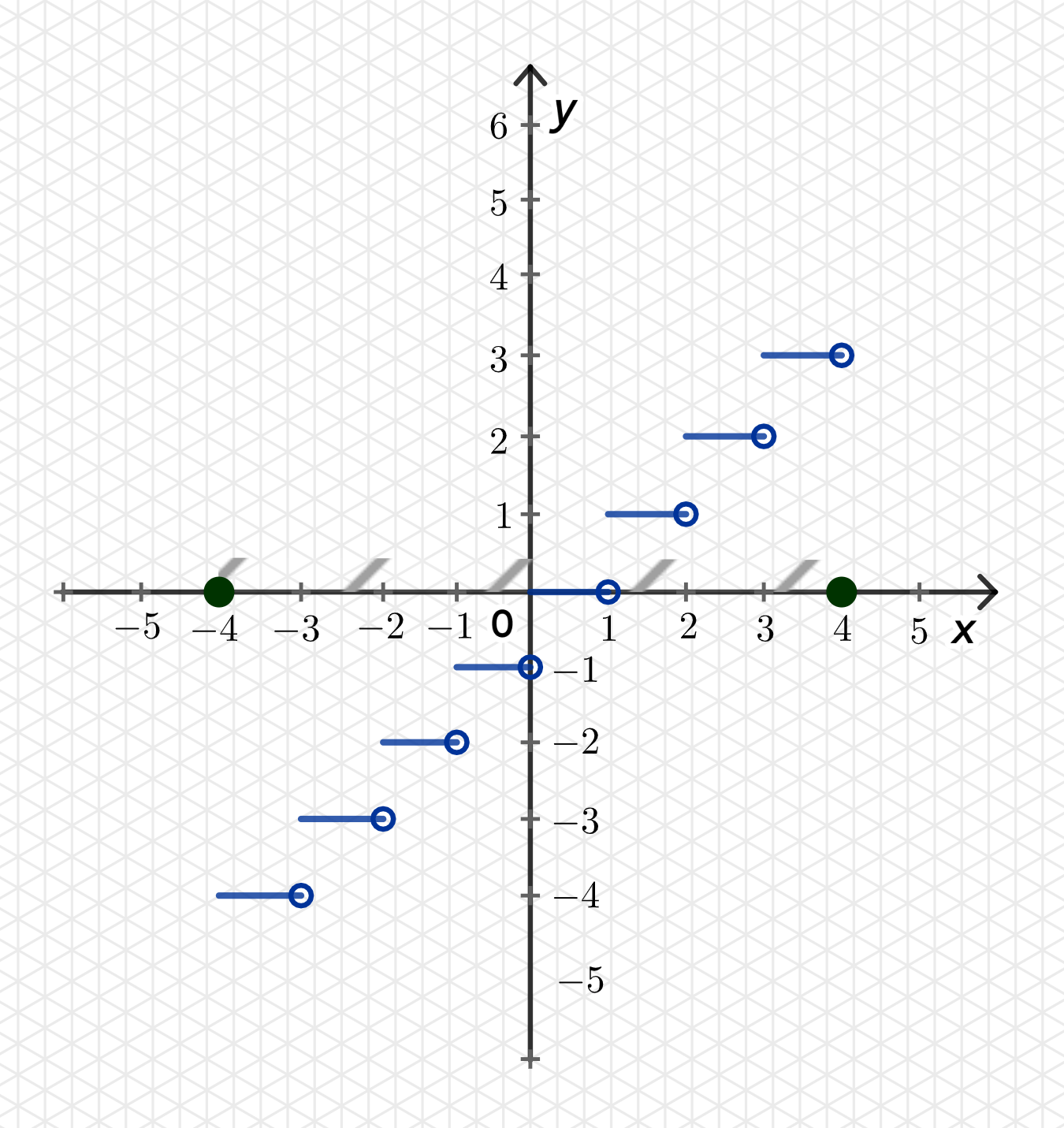
Функция $y = [x]$ будет выглядеть как лестница, которая на каждом интервале между целыми числами принимает постоянное значение $k$. Каждая ступень будет вертикальной и начинаться с целого числа $k$ и заканчиваться в $k+1$, не включая $k+1$.

На отрезке $[-4; 4]$ будут следующие интервалы:

• $y = -4$ для $x \in [-4, -3)$,
• $y = -3$ для $x \in [-3, -2)$,
• $y = -2$ для $x \in [-2, -1)$,
• $y = -1$ для $x \in [-1, 0)$,
• $y = 0$ для $x \in [0, 1)$,
• $y = 1$ для $x \in [1, 2)$,
• $y = 2$ для $x \in [2, 3)$,
• $y = 3$ для $x \in [3, 4)$.

б) $y = [1 — x]$

Шаг 1. Определение целой части выражения $1 — x$

Мы рассматриваем функцию $y = [1 — x]$, то есть целую часть выражения $1 — x$. Для того, чтобы построить график этой функции, нужно понять, как изменяется целая часть выражения $1 — x$ при изменении $x$.

Для $1 — x$ целая часть будет зависеть от того, на каком интервале находится $1 — x$. То есть:

$$k \leq 1 — x < k + 1.$$

Это неравенство можно преобразовать:

$$k — 1 \leq -x < k,$$

и умножив на $-1$, получаем:

$$-k < x \leq -(k — 1).$$

Таким образом, для каждого целого $k$ на интервале $x$, функция будет принимать значение $y = k$.

Шаг 2. График функции

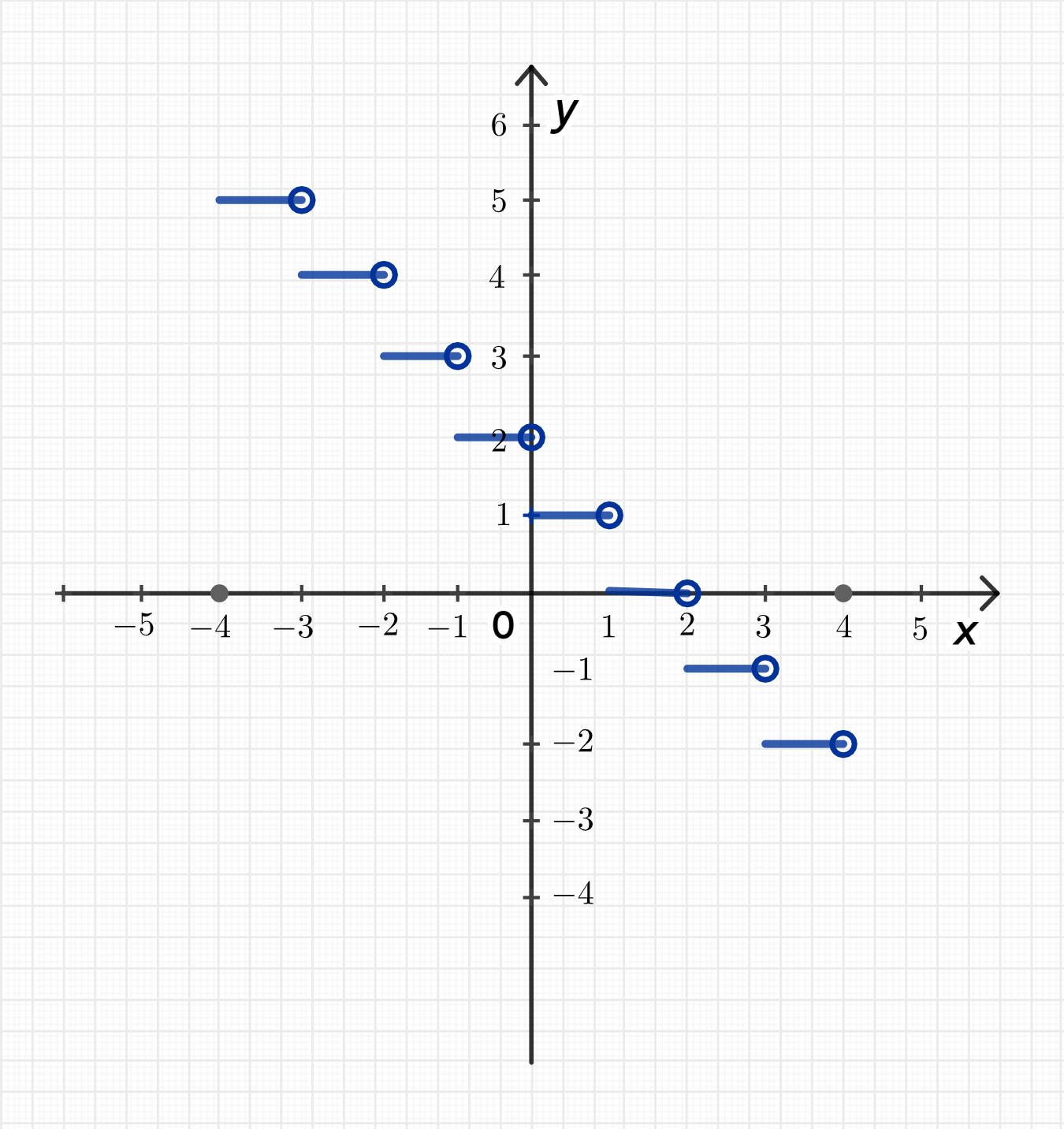
На отрезке $[-4; 4]$ функция будет меняться следующим образом:

• Для $x \in (-4, -3]$, $1 — x \in (5, 4]$, $y = 4$,
• Для $x \in (-3, -2]$, $1 — x \in (4, 3]$, $y = 3$,
• Для $x \in (-2, -1]$, $1 — x \in (3, 2]$, $y = 2$,
• Для $x \in (-1, 0]$, $1 — x \in (2, 1]$, $y = 1$,
• Для $x \in (0, 1]$, $1 — x \in (1, 0]$, $y = 0$,
• Для $x \in (1, 2]$, $1 — x \in (0, -1]$, $y = -1$,
• Для $x \in (2, 3]$, $1 — x \in (-1, -2]$, $y = -2$,
• Для $x \in (3, 4]$, $1 — x \in (-2, -3]$, $y = -3$.

в) $y = [x + 4]$

Шаг 1. Определение целой части выражения $x + 4$

Для функции $y = [x + 4]$ целая часть будет зависеть от выражения $x + 4$. Рассмотрим, как $[x + 4]$ изменяется в зависимости от $x$:

$$k \leq x + 4 < k + 1.$$

Решим это неравенство для $x$:

$$k — 4 \leq x < k — 3.$$

Шаг 2. График функции

На отрезке $[-4; 4]$ значения функции будут следующими:

• $y = 0$ для $x \in [-4, -3)$,
• $y = 1$ для $x \in [-3, -2)$,
• $y = 2$ для $x \in [-2, -1)$,
• $y = 3$ для $x \in [-1, 0)$,
• $y = 4$ для $x \in [0, 1)$,
• $y = 5$ для $x \in [1, 2)$,
• $y = 6$ для $x \in [2, 3)$,
• $y = 7$ для $x \in [3, 4)$.

г) $y = \left[\frac{1 — x}{2}\right]$

Шаг 1. Определение целой части выражения $\frac{1 — x}{2}$

Для функции $y = \left[\frac{1 — x}{2}\right]$, целая часть будет зависеть от выражения $\frac{1 — x}{2}$. Рассмотрим это неравенство:

$$k \leq \frac{1 — x}{2} < k + 1.$$

Умножим обе части на 2:

$$2k \leq 1 — x < 2k + 2.$$

Теперь решим относительно $x$:

$$2k — 1 \leq -x < 2k + 1,$$

умножим на $-1$:

$$-(2k + 1) < x \leq -(2k — 1).$$

Шаг 2. График функции

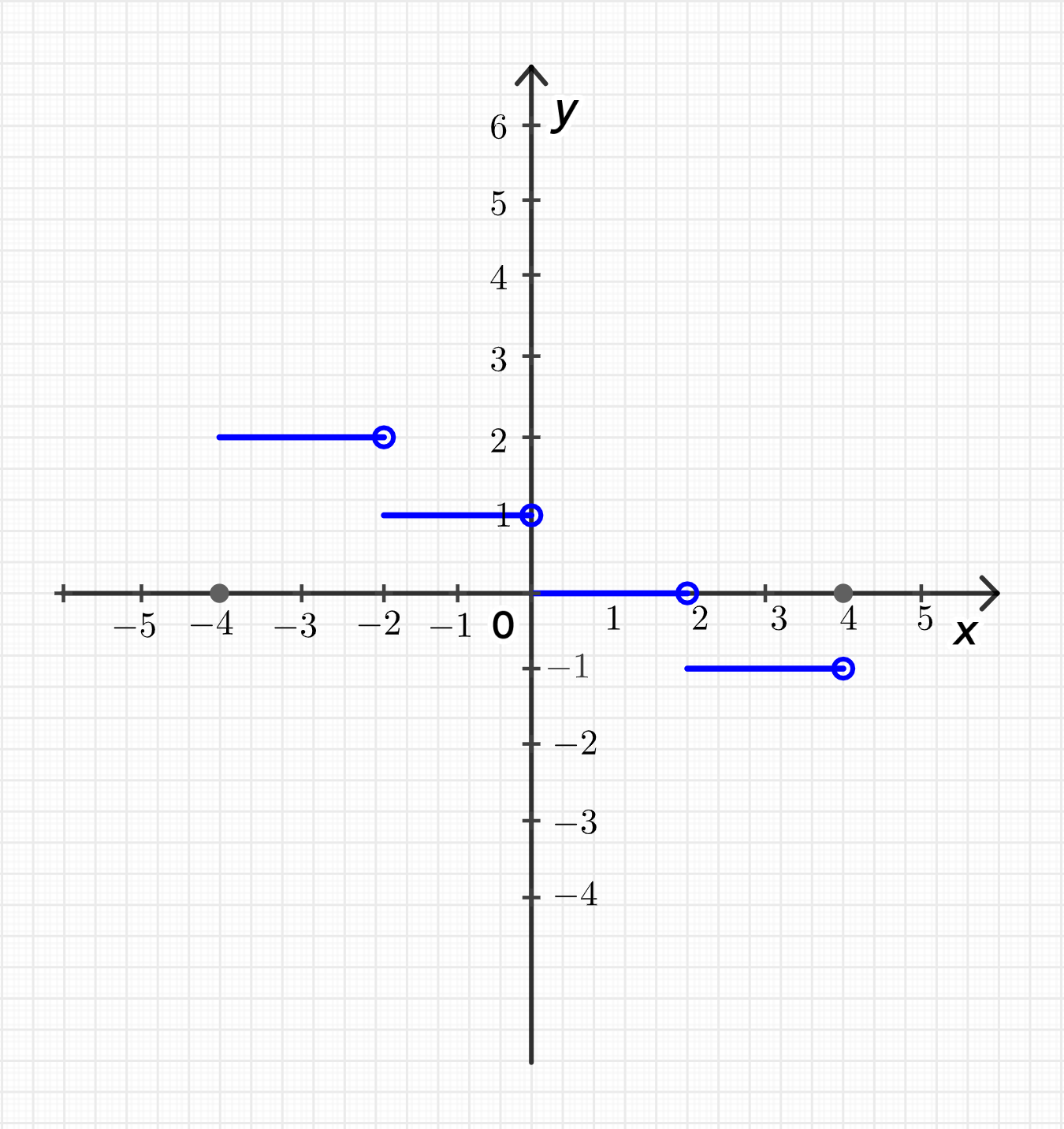
На отрезке $[-4; 4]$ функция будет иметь следующие значения:

• $y = -2$ для $x \in [-4, -3)$,
• $y = -1$ для $x \in [-3, -2)$,
• $y = 0$ для $x \in [-2, -1)$,
• $y = 1$ для $x \in [-1, 0)$,
• $y = 2$ для $x \in [0, 1)$,
• $y = 3$ для $x \in [1, 2)$,
• $y = 4$ для $x \in [2, 3)$,
• $y = 5$ для $x \in [3, 4)$.

Итоговые ответы:

а) График функции $y = [x]$ представляет собой лестницу с горизонтальными участками на интервалах между целыми числами.

б) График функции $y = [1 — x]$ представляет собой лестницу, сдвинутую относительно функции $y = [x]$.

в) График функции $y = [x + 4]$ представляет собой лестницу, сдвинутую на 4 единицы вправо.

г) График функции $y = \left[\frac{1 — x}{2}\right]$ также представляет собой лестницу, но с более сложным сдвигом.