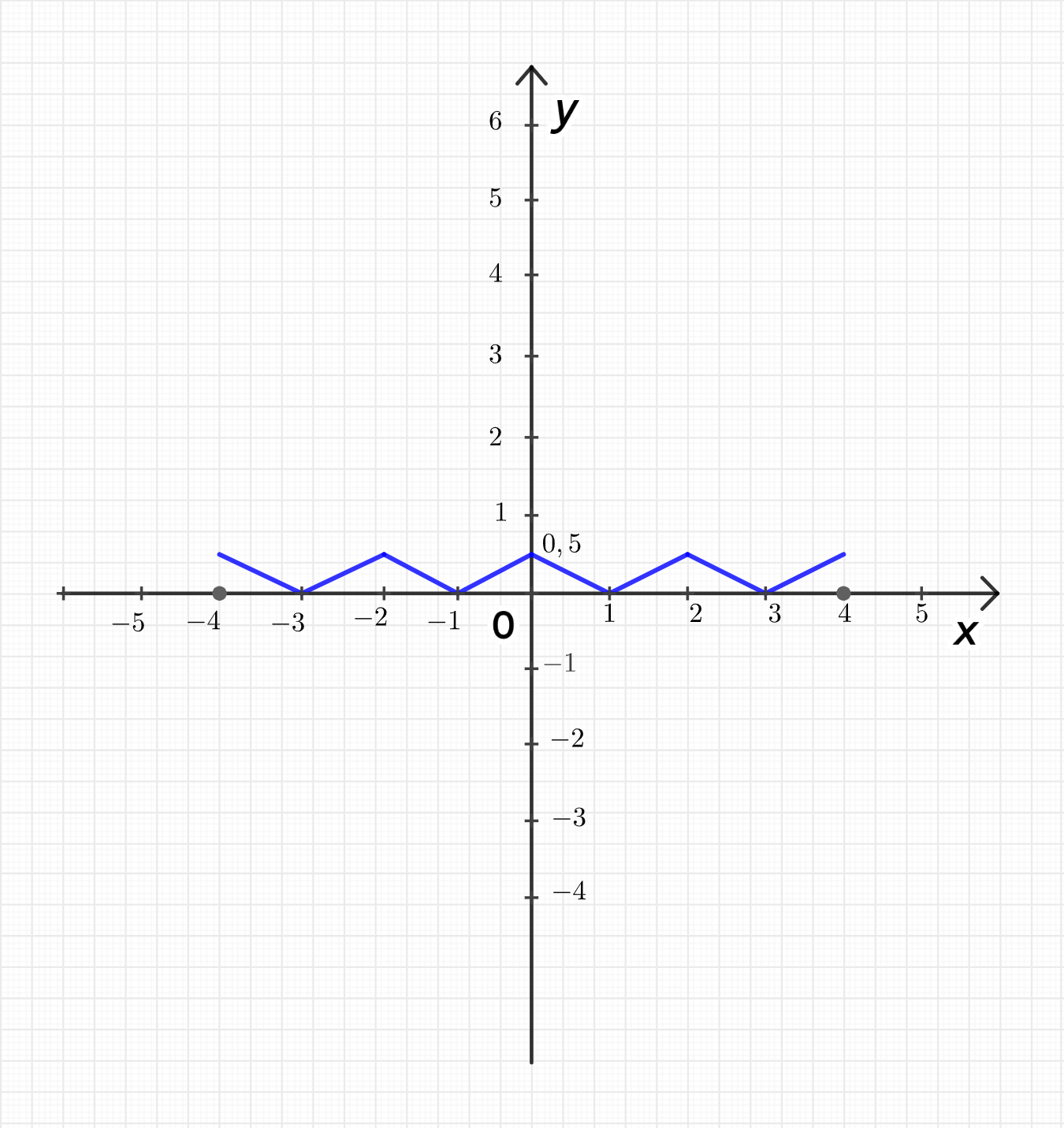ГДЗ по Алгебре 10 Класс Номер 7.74 Профильный Уровень Мордкович — Подробные Ответы

Построить график заданной функции на отрезке $[-4; 4]$:

а) $y = \{x\} = x — [x]$;

б) $y = \{1 — x\} = (1 — x) — [1 — x]$;

в) $y = \{x + 4\} = (x + 4) — [x + 4]$;

г) $y = \left\{\frac{1 — x}{2}\right\} = \frac{1 — x}{2} — \left[\frac{1 — x}{2}\right]$

Построить график заданной функции на отрезке $[-4; 4]$:

а) $y = \{x\} = x — [x]$;

Пусть $[x] = k$, тогда:

$$k \leq x < k + 1;$$ $$0 \leq y < 1;$$

График функции:

б) $y = \{1 — x\} = (1 — x) — [1 — x]$;

Пусть $[1 — x] = k$, тогда:

$$k \leq 1 — x < k + 1;$$ $$-(k + 1) \leq -x < -k;$$ $$-k < x \leq -(k — 1);$$ $$0 \leq y < 1;$$

График функции:

в) $y = \{x + 4\} = (x + 4) — [x + 4]$;

Пусть $[x + 4] = k$, тогда:

$$k \leq x + 4 < k + 1;$$ $$k — 4 \leq x < k — 3;$$ $$0 \leq y < 1;$$

График функции:

г) $y = \left\{\frac{1 — x}{2}\right\} = \frac{1 — x}{2} — \left[\frac{1 — x}{2}\right]$;

Пусть $\left[\frac{1 — x}{2}\right] = k$, тогда:

$$k \leq \frac{1 — x}{2} < k + 1;$$ $$2k \leq 1 — x < 2k + 2;$$ $$2k — 1 \leq -x < 2k + 1;$$ $$-(2k + 1) < x \leq -(2k — 1);$$ $$0 \leq y < 1;$$

График функции:

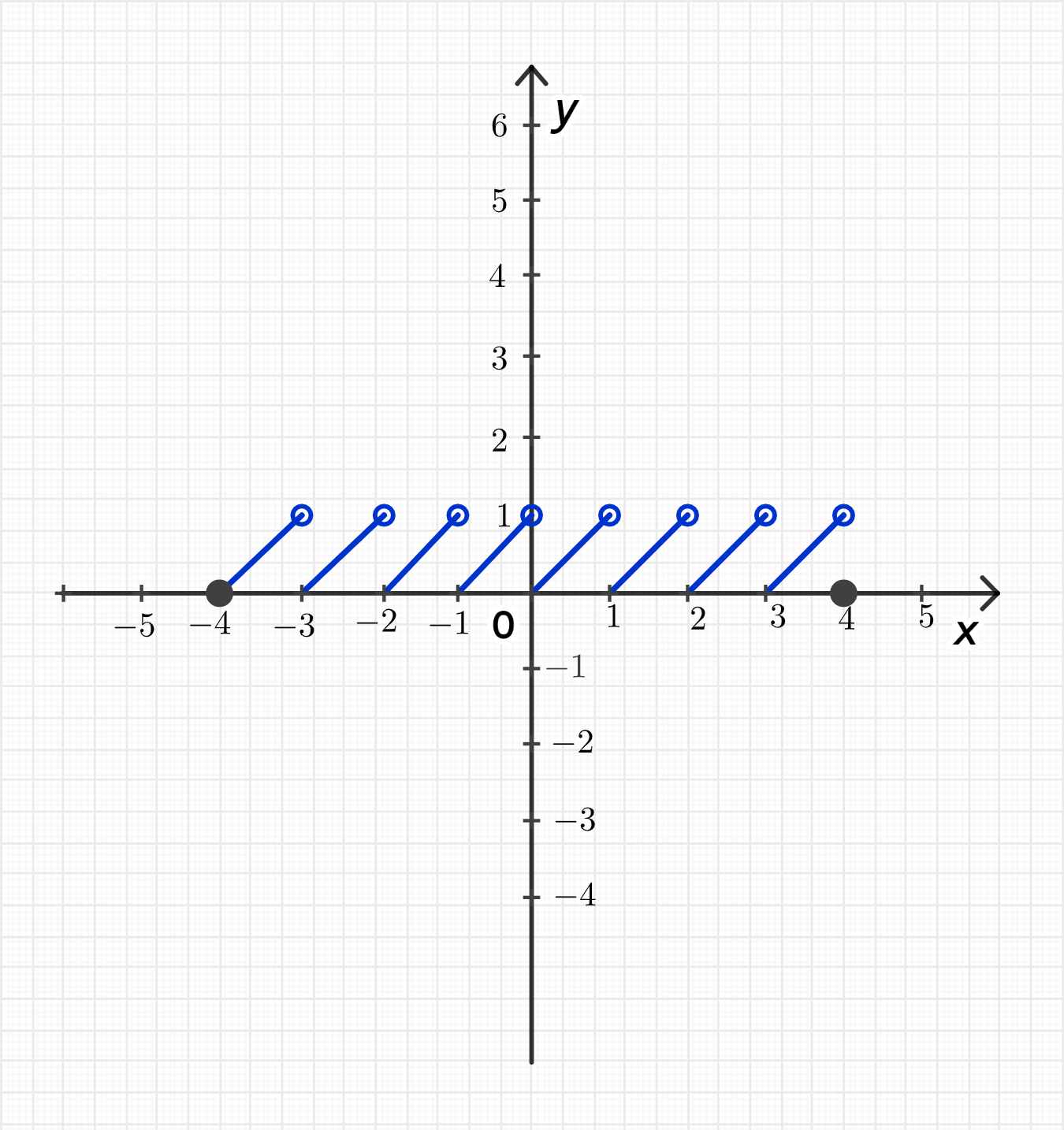
а) $y = \{x\} = x — [x]$

Шаг 1. Определение дробной части числа

Дробная часть числа $x$, обозначаемая $\{x\}$, определяется как разница между числом $x$ и его целой частью $[x]$. То есть:

$$\{x\} = x — [x],$$

где $[x]$ — это целая часть числа $x$, наибольшее целое число, не превосходящее $x$. Например:

• Если $x = 2.5$, то $[x] = 2$, а $\{x\} = 0.5$.
• Если $x = -1.3$, то $[x] = -2$, а $\{x\} = 0.7$.

Шаг 2. Для функции $y = \{x\}$

Мы хотим построить график функции $y = \{x\}$, то есть дробной части числа $x$. На каждом интервале между целыми числами, функция будет принимать значения от 0 до 1, не включая 1, и будет изменяться линейно.

Для любого $x$, которое лежит в интервале $[k, k+1)$, где $k$ — целое число, дробная часть $\{x\}$ будет равна:

$$\{x\} = x — [x] = x — k, \quad \text{где} \, x \in [k, k+1).$$

Это означает, что на каждом интервале $[k, k+1)$, функция $y = \{x\}$ будет увеличиваться от 0 до 1.

Шаг 3. График функции

График функции $y = \{x\}$ — это серия отрезков, каждый из которых начинается в точке $(k, 0)$ и заканчивается в точке $(k+1, 1)$, но не включая $k+1$. Функция будет «скакать» от 0 до 1 на каждом интервале $[k, k+1)$, образуя ступенчатую кривую.

Для отрезка $[-4, 4]$ график будет следующим:

• $y = 0$ для $x \in [-4, -3)$,
• $y = 0.5$ для $x \in [-3, -2)$,
• $y = 0.7$ для $x \in [-2, -1)$,
• $y = 1$ для $x \in [0, 1)$,
  и так далее.

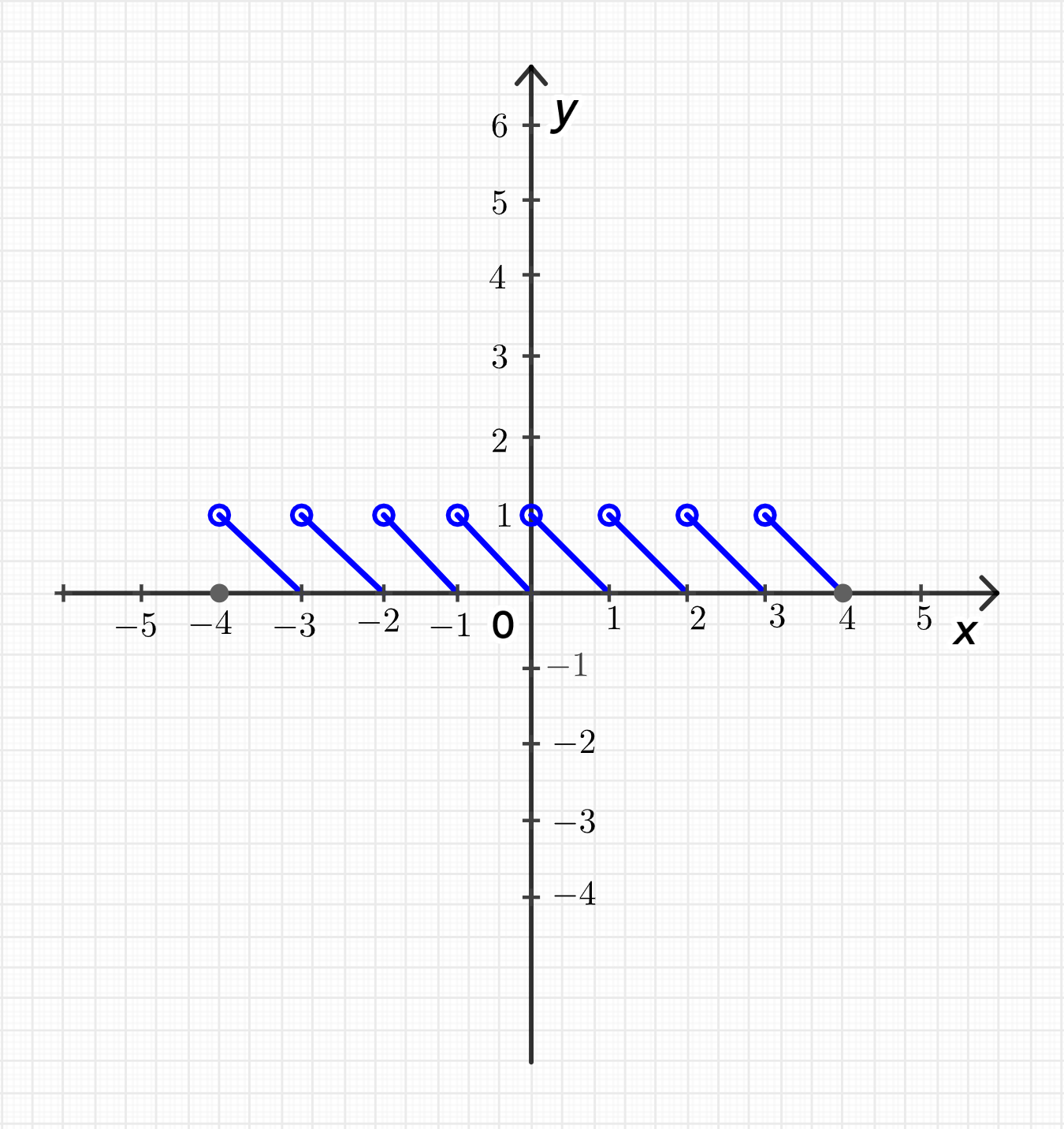
б) $y = \{1 — x\} = (1 — x) — [1 — x]$

Шаг 1. Преобразование функции

Для $y = \{1 — x\}$, нам нужно разобраться с выражением $1 — x$. Пусть $[1 — x] = k$ — целая часть выражения $1 — x$. Тогда для любого $x$, мы имеем:

$$k \leq 1 — x < k + 1.$$

Теперь преобразуем неравенство, чтобы выразить $x$ через $k$:

$$k — 1 \leq -x < k \quad \Rightarrow \quad -k < x \leq -(k — 1).$$

Таким образом, для каждого целого $k$, дробная часть $\{1 — x\}$ будет изменяться от 0 до 1.

Шаг 2. График функции

Функция $y = \{1 — x\}$ будет аналогична функции $y = \{x\}$, но с преобразованием по оси $x$. График будет состоять из интервалов, аналогичных тем, что мы получили для функции $y = \{x\}$, только сдвинутых в зависимости от значений $1 — x$.

Для отрезка $[-4, 4]$ функция $y = \{1 — x\}$ будет иметь следующие значения:

• $y = 0$ для $x \in (-4, -3]$,
• $y = 0.5$ для $x \in (-3, -2]$,
• $y = 0.7$ для $x \in (-2, -1]$,
• $y = 1$ для $x \in [0, 1]$,
  и так далее.

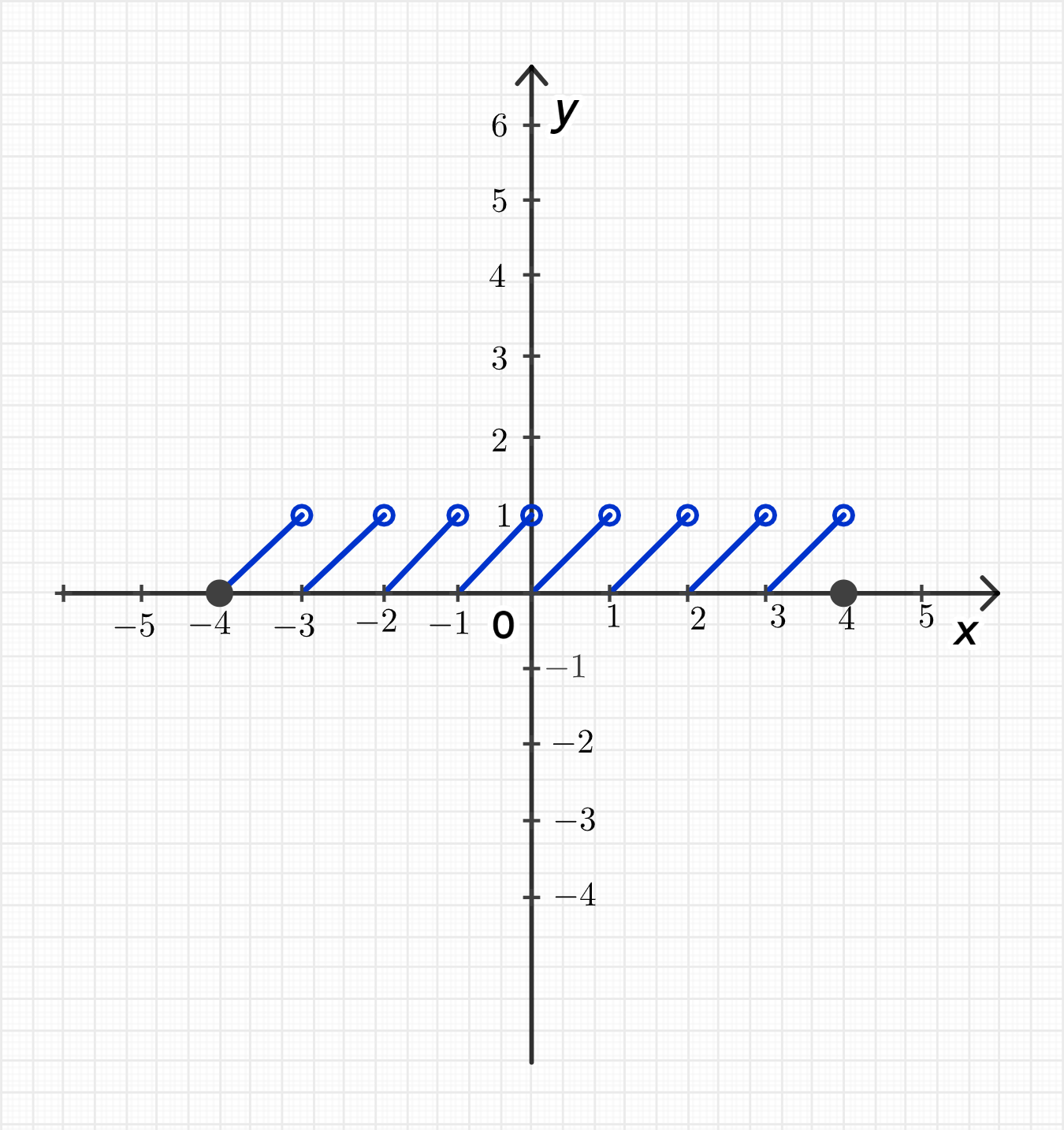
в) $y = \{x + 4\} = (x + 4) — [x + 4]$

Шаг 1. Преобразование функции

Для $y = \{x + 4\}$, дробная часть будет зависеть от $x + 4$. Если $[x + 4] = k$, то:

$$k \leq x + 4 < k + 1.$$

Преобразуем это неравенство для $x$:

$$k — 4 \leq x < k — 3.$$

Теперь дробная часть функции будет изменяться от 0 до 1 на каждом интервале $[k — 4, k — 3)$.

Шаг 2. График функции

Функция $y = \{x + 4\}$ будет также иметь ступенчатый вид, сдвинутый на 4 единицы вправо относительно функции $y = \{x\}$. Она будет принимать значения от 0 до 1 на каждом интервале, соответствующем целым числам $k$, но сдвинутым на 4.

Для отрезка $[-4, 4]$ значения функции будут:

• $y = 0$ для $x \in [-4, -3]$,
• $y = 0.5$ для $x \in [-3, -2]$,
• $y = 1$ для $x \in [-2, -1]$,
  и так далее.

г) $y = \left\{\frac{1 — x}{2}\right\} = \frac{1 — x}{2} — \left[\frac{1 — x}{2}\right]$

Шаг 1. Преобразование функции

Для $y = \left\{\frac{1 — x}{2}\right\}$, дробная часть будет зависеть от выражения $\frac{1 — x}{2}$. Пусть $\left[\frac{1 — x}{2}\right] = k$, тогда:

$$k \leq \frac{1 — x}{2} < k + 1.$$

Умножим обе части на 2:

$$2k \leq 1 — x < 2k + 2.$$

Преобразуем это для $x$:

$$2k — 1 \leq -x < 2k + 1 \quad \Rightarrow \quad -(2k + 1) < x \leq -(2k — 1).$$

Шаг 2. График функции

Функция $y = \left\{\frac{1 — x}{2}\right\}$ будет иметь аналогичный ступенчатый вид, но с более сложным сдвигом, в зависимости от выражения $\frac{1 — x}{2}$.

Для отрезка $[-4, 4]$ значения функции будут:

• $y = 0$ для $x \in [-4, -3]$,
• $y = 0.5$ для $x \in [-3, -2]$,
• $y = 1$ для $x \in [-2, -1]$,
  и так далее.

Итоговые ответы:

а) График функции $y = \{x\}$ представляет собой лестницу, принимающую значения от 0 до 1 на каждом интервале.

б) График функции $y = \{1 — x\}$ также является лестницей, но сдвинутой по оси $x$.

в) График функции $y = \{x + 4\}$ представляет собой лестницу, сдвинутую на 4 единицы вправо.

г) График функции $y = \left\{\frac{1 — x}{2}\right\}$ также будет лестницей, но с более сложным сдвигом.