ГДЗ по Алгебре 10 Класс Номер 7.9 Профильный Уровень Мордкович — Подробные Ответы

Ha рисунке представлен график функции, определенной на отрезке [а; b]; S(x) — площадь «подграфика» на отрезке [а; x], а < x < b. Выразите величину S(x) через x и постройте график функции у = S(x). По этому графику найдите область значений функции у = S(x):

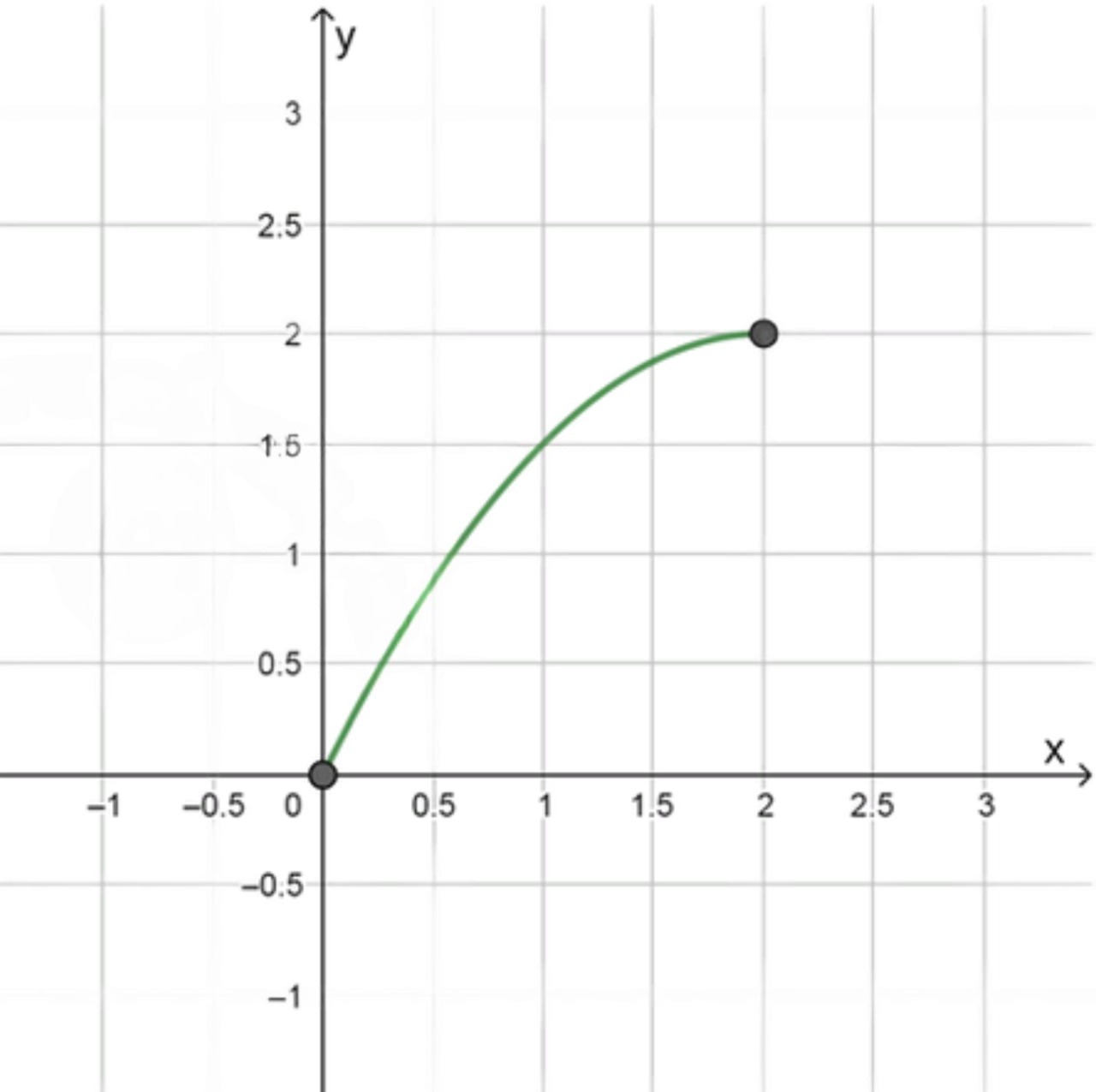
а) рис. 8 (а = 0, b = 2);

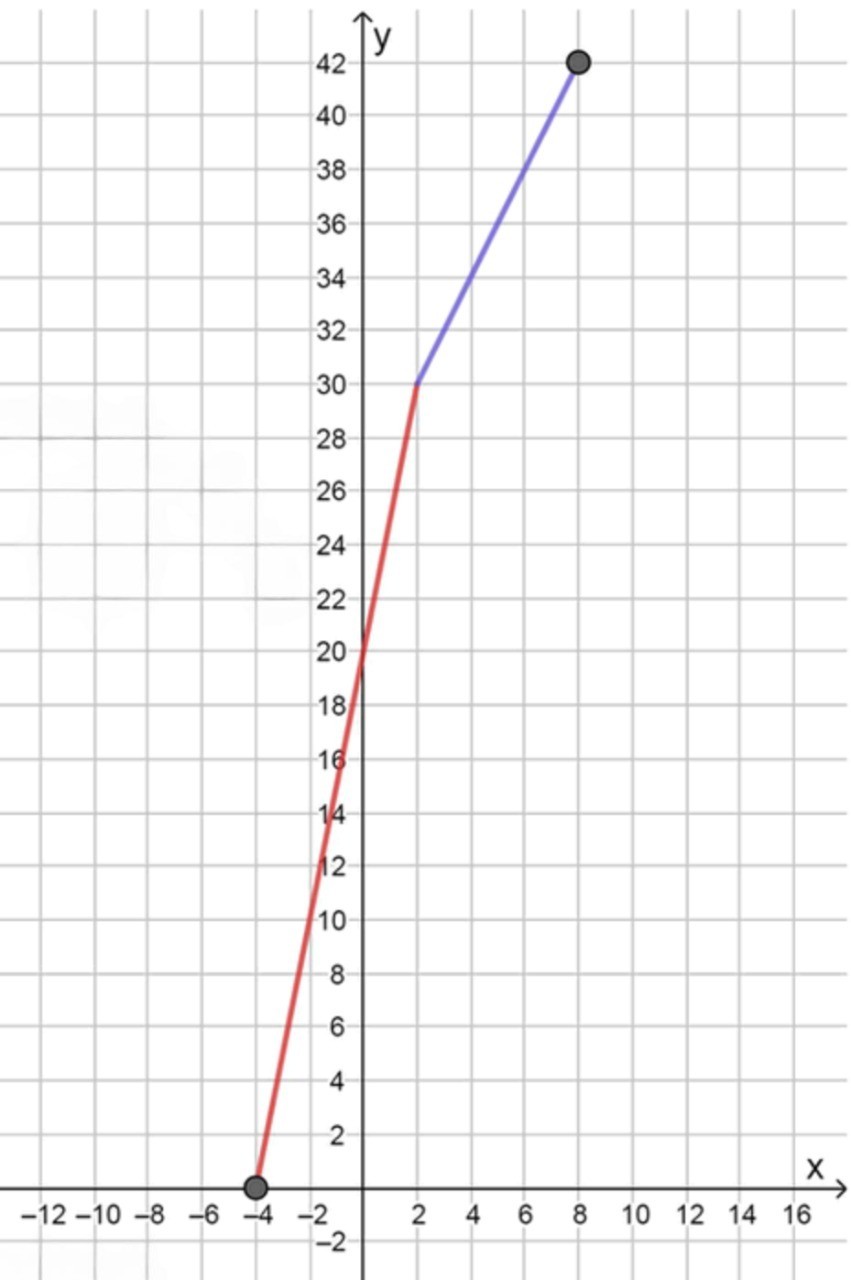
б) рис. 9 (а = -4, b = 8).

а) Рисунок 8 ($a = 0, b = 2$):

Прямая задана функцией вида $y = kx + b$:

$$\begin{cases} 2 = k \cdot 0 + b & \Rightarrow \begin{cases} b = 2 \\ 0 = k \cdot 2 + b \end{cases} \Rightarrow \begin{cases} b = 2 \\ k = -1 \end{cases}; \end{cases}$$ $$y = -x + 2 = 2 — x;$$

Под графиком функции имеем трапецию, у которой $a = 2$, $b = 2 — x$ и $h = x$:

$$S(x) = \frac{h(a + b)}{2} = \frac{x(2 + (2 — x))}{2} = \frac{x(4 — x)}{2};$$

График искомой функции:

Множество значений функции: $E(f) = [0; 2]$;

Ответ: $S(x) = \frac{x(4 — x)}{2}, \, x \in [0; 2]$.

б) Рисунок 9 ($a = -4, b = 8$):

Под графиком имеем многоугольник, состоящий из двух прямоугольников, стороны которых равны:

$$a_1 = 2 — (-4) = 2 + 4 = 6 \quad \text{и} \quad b_1 = 5 — 0 = 5;$$ $$a_2 = 8 — 2 = 6 \quad \text{и} \quad b_2 = 2 — 0 = 2;$$

Если $-4 \leq x \leq 2$, тогда:

$$S(x) = (x — (-4)) \cdot b_1 = 5(x + 4) = 5x + 20;$$

Если $2 < x \leq 8$, тогда:

$$S_1 = a_1 \cdot b_1 = 6 \cdot 5 = 30;$$ $$S_2 = (x — 2) \cdot b_2 = 2(x — 2) = 2x — 4;$$ $$S(x) = S_1 + S_2 = 30 + 2x — 4 = 2x + 26;$$

График искомой функции:

Множество значений функции: $E(f) = [0; 42]$;

Ответ:

$$S(x) = \begin{cases} 5x + 20, \text{если } -4 \leq x \leq 2 \\ 2x + 26, \text{если } 2 < x \leq 8 \end{cases}.$$

а) Рисунок 8 $(a = 0, b = 2)$

1) Найдём уравнение прямой

Нам дана прямая линия, проходящая через две точки:

• $A(0, 2)$
• $B(2, 0)$

Прямая описывается уравнением линейной функции:

$$y = kx + b$$

Где:

• $k$ — угловой коэффициент (наклон прямой),
• $b$ — значение $y$ при $x = 0$ (сдвиг по оси $y$).

Подставим точку $A(0, 2)$:

$$2 = k \cdot 0 + b \Rightarrow b = 2$$

Подставим точку $B(2, 0)$:

$$0 = k \cdot 2 + 2 \Rightarrow 2k = -2 \Rightarrow k = -1$$

Итоговое уравнение прямой:

$$y = -x + 2$$

2) Найдём площадь фигуры под графиком

Под графиком на отрезке $x \in [0, 2]$ находится трапеция. Границы по оси $x$ — от 0 до 2.

Вспомним формулу площади трапеции:

$$S = \frac{1}{2} h (a + b)$$

Где:

• $h$ — высота трапеции (в данном случае $x$),
• $a$ — длина одного основания трапеции,
• $b$ — длина второго основания трапеции.

Поскольку одно основание — это постоянная высота $y = 2$, а второе основание — значение функции $y = 2 — x$, то:

• $a = 2$ (высота слева при $x = 0$),
• $b = 2 — x$ (значение функции в правой точке),
• $h = x$

Подставим в формулу:

$$S(x) = \frac{1}{2} \cdot x \cdot (2 + (2 — x)) = \frac{1}{2} \cdot x \cdot (4 — x)$$ $$S(x) = \frac{x(4 — x)}{2}$$

3) График функции $S(x)$

Функция $S(x) = \frac{x(4 — x)}{2}$ определена на отрезке:

$$x \in [0; 2]$$

Это квадратичная функция, ветви параболы направлены вниз, так как коэффициент при $x^2$ отрицателен:

$$S(x) = \frac{-x^2 + 4x}{2} = -\frac{1}{2}x^2 + 2x$$

4) Найдём множество значений функции

Функция определена на отрезке $[0; 2]$. Найдём максимум функции на этом промежутке.

$$S(x) = \frac{x(4 — x)}{2}$$

Максимум будет в вершине параболы, а вершина у квадратичной функции $y = ax^2 + bx + c$ достигается при:

$$x = -\frac{b}{2a}$$

В нашей функции:

$$S(x) = -\frac{1}{2}x^2 + 2x \Rightarrow a = -\frac{1}{2}, b = 2 \Rightarrow x = -\frac{2}{2 \cdot (-\frac{1}{2})} = 2$$

Подставим $x = 2$ в функцию:

$$S(2) = \frac{2(4 — 2)}{2} = \frac{2 \cdot 2}{2} = 2$$

Минимальное значение:

$$S(0) = \frac{0 \cdot 4}{2} = 0$$

Ответ:

Множество значений:

$$E(f) = [0; 2]$$

Окончательный ответ для пункта (а):

$$S(x) = \frac{x(4 — x)}{2}, \quad x \in [0; 2]$$

б) Рисунок 9 $(a = -4, b = 8)$

На рисунке — фигура под графиком, составленная из двух прямоугольников.

1) Разделим на части:

• От $x = -4$ до $x = 2$: прямоугольник высотой 5.
• От $x = 2$ до $x = 8$: прямоугольник высотой 2.

Найдём стороны этих прямоугольников:

Прямоугольник 1:

• Ширина: $a_1 = 2 — (-4) = 6$
• Высота: $b_1 = 5 — 0 = 5$

Прямоугольник 2:

• Ширина: $a_2 = 8 — 2 = 6$
• Высота: $b_2 = 2 — 0 = 2$

2) Первая часть графика: $-4 \leq x \leq 2$

На этом участке площадь под графиком линейно нарастает.

Ширина области от левого края ($x = -4$) до текущего $x$:

$$x — (-4) = x + 4$$

Площадь прямоугольника:

$$S(x) = 5 \cdot (x + 4) = 5x + 20$$

3) Вторая часть графика: $2 < x \leq 8$

Теперь площадь состоит из двух частей:

1. Постоянная площадь слева (вся отрезанная область до $x = 2$):

$$S_1 = a_1 \cdot b_1 = 6 \cdot 5 = 30$$

2. Новая площадь справа:

Ширина новой области: $x — 2$

Высота: 2

$$S_2 = 2(x — 2) = 2x — 4$$

Общая площадь:

$$S(x) = S_1 + S_2 = 30 + (2x — 4) = 2x + 26$$

4) Найдём множество значений

Минимум площади — в крайней левой точке, где $x = -4$:

$$S(-4) = 5 \cdot (-4 + 4) = 0$$

Максимум — в крайней правой точке $x = 8$:

$$S(8) = 2 \cdot 8 + 26 = 42$$

Ответ:

Множество значений:

$$E(f) = [0; 42]$$

Окончательный ответ для пункта (б):

$$S(x) = \begin{cases} 5x + 20, & \text{если } -4 \leq x \leq 2 \\ 2x + 26, & \text{если } 2 < x \leq 8 \end{cases}$$