ГДЗ по Алгебре 10 Класс Номер 9.17 Профильный Уровень Мордкович — Подробные Ответы

Постройте график данной периодической функции у = f(x) и укажите область ее определения, область значений, промежутки монотонности, точки экстремума, наибольшее и наименьшее значения, нули функции, промежутки знаков постоянства; исследуйте функцию на четность-нечетность:

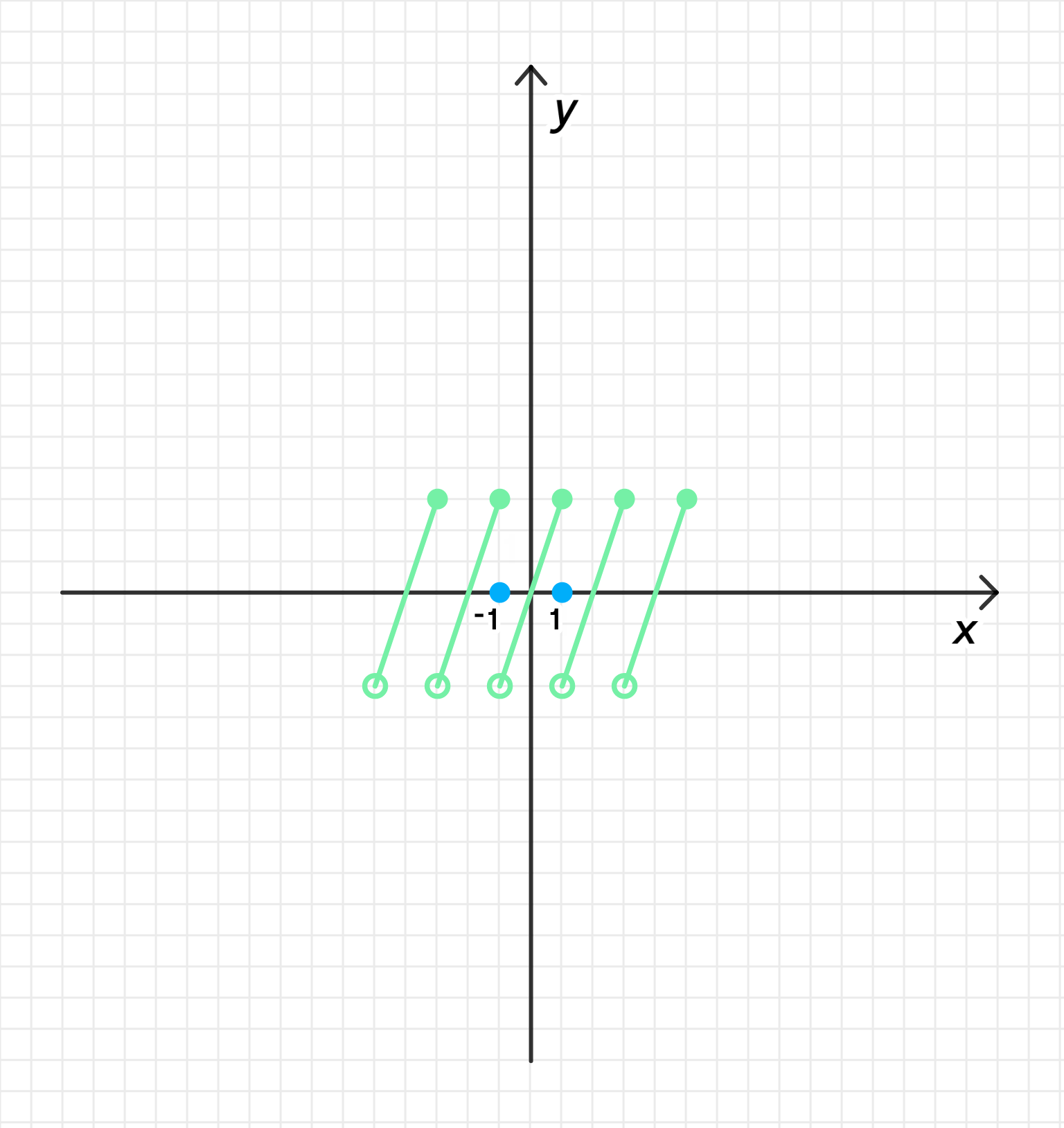
а) Период функции равен 2 и f(x) = Sx на промежутке (-1; 1];

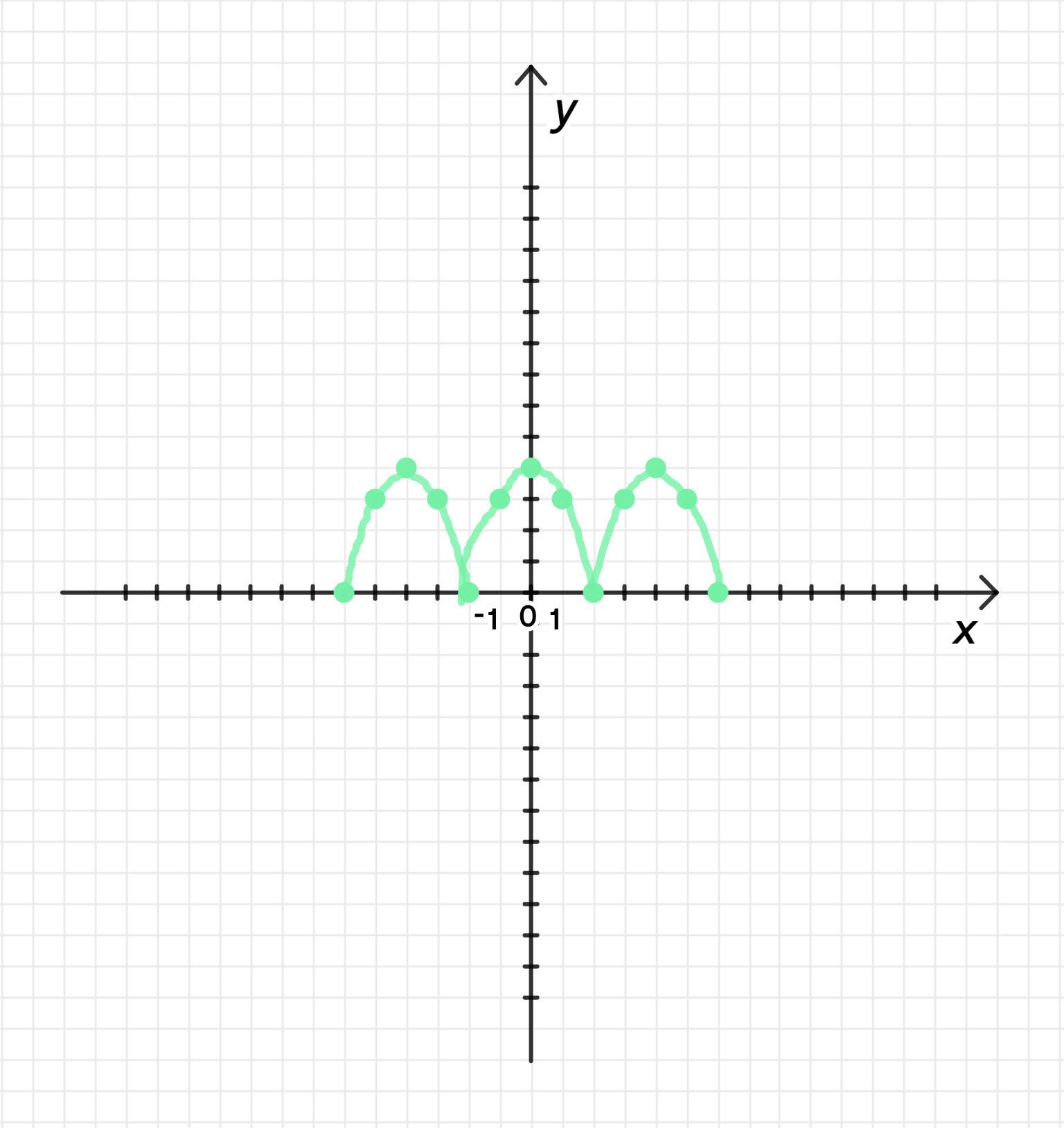
б) период функции равен 4 и f(x) = 4 — x² на отрезке [-2; 2];

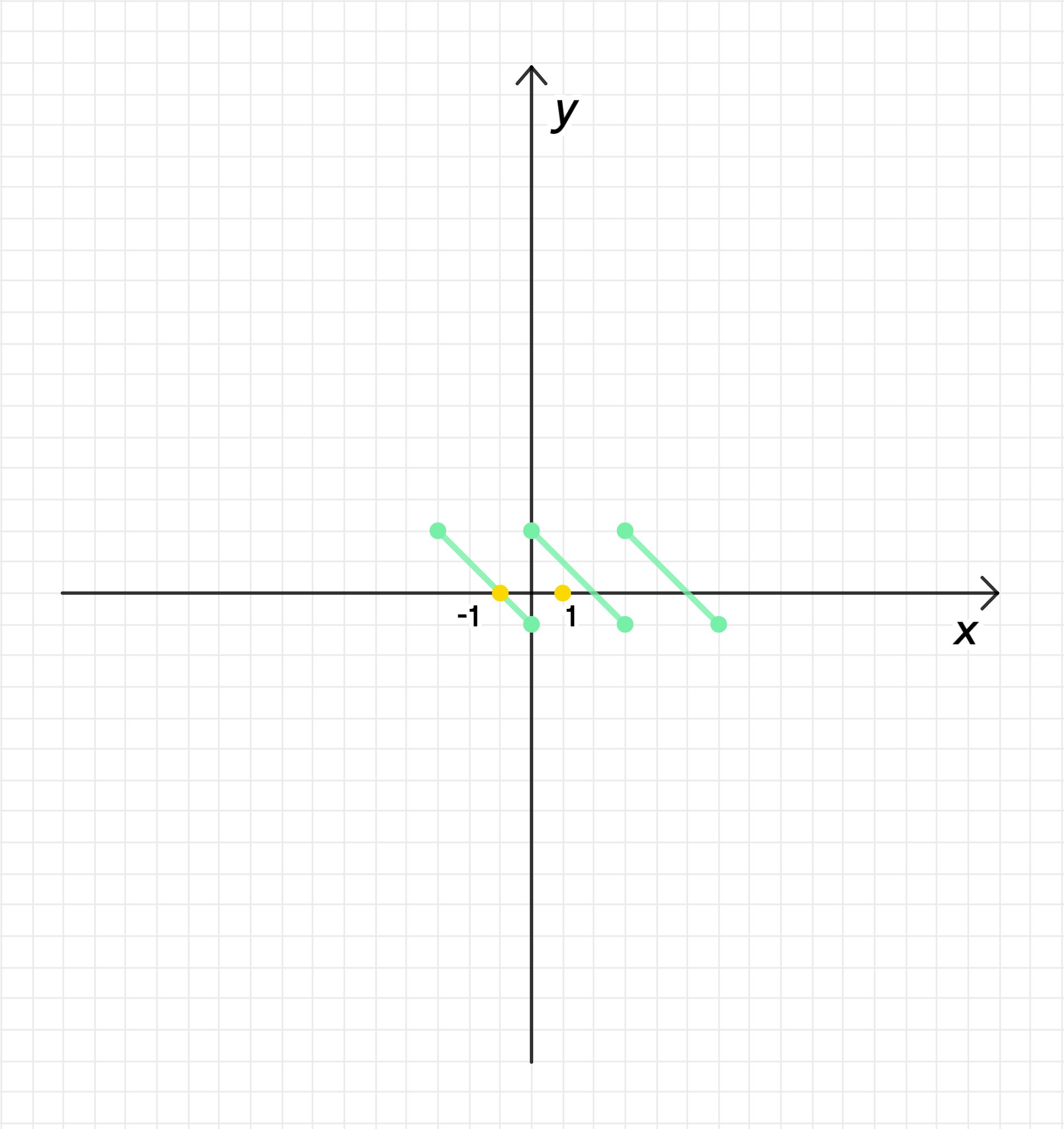
в) период функции равен 3 и f{x) = 2 — x на промежутке [0; 3);

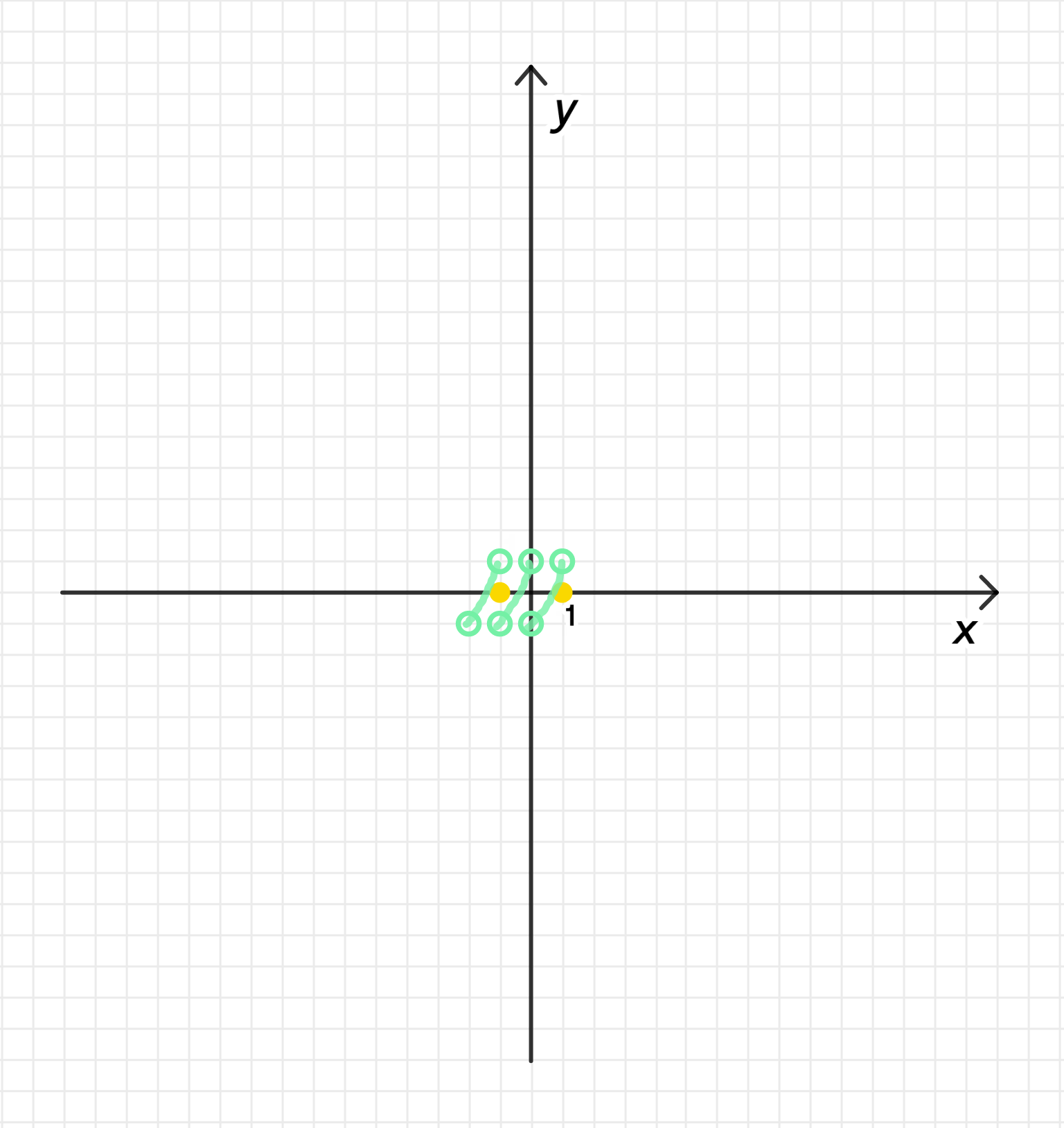
г) период функции равен 1 и f(x) = 2x² — 1 на промежутке (0; 1).

а) $f(x) = 3x$ на промежутке $(-1; 1]$ и $T = 2$:

Рассмотрим функцию $y = 3x$:

• $k = 3 > 0$ — функция возрастает;
• $3x = 0 \quad \Rightarrow \quad x = 0$;

Все периоды функции:

• $T_{\text{общ}} = kT = 2k$;

График функции:

Область определения: $D(f) = (-\infty; +\infty)$;

Множество значений: $E(f) = (-3; 3]$;

Возрастает на $(2k — 1; 2k + 1]$;

Наибольшее и наименьшее значения:

• $y_{\text{наиб}} = 3$ и $y_{\text{наим}}$ — нет;

Нули функции: $x = 2k$;

$f(x) > 0$ на $(2k; 2k + 1]$ и $f(x) < 0$ на $(2k — 1; 2k)$;

Функция ни четная, ни нечетная;

б) $f(x) = 4 — x^2$ на отрезке $[-2; 2]$ и $T = 4$:

Рассмотрим функцию $y = 4 — x^2$:

• $a = -1 < 0$ — ветви направлены вниз;
• $x_0 = -\frac{b}{2a} = -\frac{0}{2 \cdot (-1)} = 0$;
• $y_0 = 4 — 0^2 = 4$;
• $4 — x^2 = 0 \quad \Rightarrow \quad x = \pm 2$;

Все периоды функции:

• $T_{\text{общ}} = kT = 4k$;

График функции:

Область определения: $D(f) = (-\infty; +\infty)$;

Множество значений: $E(f) = [0; 4]$;

Возрастает на $[4k — 2; 4k]$ и убывает на $[4k; 4k + 2]$;

Наибольшее и наименьшее значения:

• $y_{\text{наиб}} = 4$ и $y_{\text{наим}} = 0$;

Нули функции: $x = 4k \pm 2$;

$f(x) > 0$ на $(4k — 2; 4k + 2)$;

Функция является четной;

в) $f(x) = 2 — x$ на промежутке $[0; 3)$ и $T = 3$:

Рассмотрим функцию $y = 2 — x$:

• $k = -1 < 0$ — функция убывает;
• $2 — x = 0 \quad \Rightarrow \quad x = 2$;

Все периоды функции:

• $T_{\text{общ}} = kT = 3k$;

График функции:

Область определения: $D(f) = (-\infty; +\infty)$;

Множество значений: $E(f) = (-1; 2]$;

Убывает на $[3k; 3k + 3)$;

Наибольшее и наименьшее значения:

• $y_{\text{наиб}} = 2$ и $y_{\text{наим}}$ — нет;

Нули функции: $x = 3k + 2$;

$f(x) > 0$ на $[3k; 3k + 2)$ и $f(x) < 0$ на $(3k + 2; 3k + 3)$;

Функция ни четная, ни нечетная;

г) $f(x) = 2x^2 — 1$ на интервале $(0; 1)$ и $T = 1$:

Рассмотрим функцию $y = 2x^2 — 1$:

• $a = 1 > 0$ — ветви направлены вверх;
• $x_0 = -\frac{b}{2a} = -\frac{0}{2 \cdot 2} = 0$;
• $y_0 = 2 \cdot 0^2 — 1 = -1$;
• $2x^2 — 1 = 0 \quad \Rightarrow \quad x^2 = 0.5 \quad \Rightarrow \quad x = \pm \frac{1}{\sqrt{2}}$;

Все периоды функции:

• $T_{\text{общ}} = kT = k$;

График функции:

Область определения: $D(f) = (k; k + 1)$;

Множество значений: $E(f) = (-1; 1)$;

Возрастает на $(k; k + 1)$;

Наибольшее и наименьшее значения:

• $y_{\text{наиб}}$ — нет и $y_{\text{наим}}$ — нет;

Нули функции: $x = k + \frac{1}{\sqrt{2}}$;

$f(x) > 0$ на $\left(k + \frac{1}{\sqrt{2}}; k + 1\right)$ и $f(x) < 0$ на $\left(k; k + \frac{1}{\sqrt{2}}\right)$;

Функция ни четная, ни нечетная;

а) $f(x) = 3x$ на промежутке $(-1; 1]$ и $T = 2$:

Шаг 1: Анализ функции $f(x) = 3x$

Функция $f(x) = 3x$ является линейной. Это значит, что её график — прямая линия.

Константа $k = 3$ — коэффициент при $x$. Так как $k > 0$, функция возрастает на всей своей области определения.

Шаг 2: Поведение функции на интервале $(-1; 1]$

Значения функции:

• Когда $x = -1$, $y = 3(-1) = -3$.
• Когда $x = 1$, $y = 3(1) = 3$.

Таблица значений:

$$\begin{array}{|c|c|c|} \hline x & -1 & 1 \\ \hline y = f(x) & -3 & 3 \\ \hline \end{array}$$

Шаг 3: Периоды функции

Поскольку функция линейна, она не имеет фиксированного периода в классическом понимании. Однако, для задачи предполагается, что период функции на этом интервале равен $T = 2$.

Таким образом, все возможные периоды для функции $f(x)$ могут быть записаны как $T_{\text{общ}} = kT = 2k$, где $k$ — целое число.

Шаг 4: График функции

Область определения: $D(f) = (-\infty; +\infty)$ — функция определена для всех $x$.

Множество значений: $E(f) = (-3; 3]$. Мы знаем, что $f(x)$ — линейная функция, она принимает значения на всей прямой.

Интервал возрастания: Поскольку $f(x)$ возрастает на всей области, то на каждом интервале $(2k — 1; 2k + 1]$ функция будет возрастать.

Наибольшее и наименьшее значения:

• $y_{\text{наиб}} = 3$ — наибольшее значение функции на интервале $(-1; 1]$.
• $y_{\text{наим}}$ — нет, так как функция возрастает, и она стремится к минус бесконечности по мере уменьшения $x$.

Нули функции: $x = 0$ — когда функция пересекает ось абсцисс, то есть $3x = 0$.

Знак функции:

• $f(x) > 0$ на интервале $(2k; 2k + 1]$.
• $f(x) < 0$ на интервале $(2k — 1; 2k)$.

Шаг 5: Четность и нечетность

Функция не является ни четной, ни нечетной, так как:

Четная функция удовлетворяет условию $f(-x) = f(x)$, что не выполняется для линейной функции $f(x) = 3x$.

Нечетная функция удовлетворяет условию $f(-x) = -f(x)$, что также не выполняется для функции $f(x) = 3x$.

б) $f(x) = 4 — x^2$ на отрезке $[-2; 2]$ и $T = 4$:

Шаг 1: Анализ функции $f(x) = 4 — x^2$

Функция $f(x) = 4 — x^2$ — это парабола, направленная вниз, так как коэффициент при $x^2$ отрицательный ($a = -1$).

Вершина параболы:

• Вершина параболы находится в точке $x_0 = -\frac{b}{2a} = 0$ (так как $b = 0$).
• Значение функции в вершине $y_0 = f(0) = 4 — 0^2 = 4$.

Шаг 2: Поведение функции на интервале $[-2; 2]$

Значения функции:

• Когда $x = -2$ или $x = 2$, $y = 4 — 2^2 = 0$.
• Когда $x = -1$ или $x = 1$, $y = 4 — 1^2 = 3$.

Таблица значений:

$$\begin{array}{|c|c|c|c|c|} \hline x & -2 & -1 & 1 & 2 \\ \hline y = f(x) & 0 & 3 & 3 & 0 \\ \hline \end{array}$$

Шаг 3: Периоды функции

Период функции равен $T = 4$, и общие периоды функции можно записать как $T_{\text{общ}} = kT = 4k$.

Шаг 4: График функции

Область определения: $D(f) = (-\infty; +\infty)$ — функция определена для всех $x$.

Множество значений: $E(f) = [0; 4]$.

Интервалы возрастания и убывания:

• Функция возрастает на интервале $[4k — 2; 4k]$.
• Функция убывает на интервале $[4k; 4k + 2]$.

Наибольшее и наименьшее значения:

• $y_{\text{наиб}} = 4$.
• $y_{\text{наим}} = 0$.

Нули функции: Функция обнуляется при $x = 4k \pm 2$, то есть при $x = -2, 2$ для $k = 0$.

Знак функции: $f(x) > 0$ на интервале $(4k — 2; 4k + 2)$.

Шаг 5: Четность функции

Функция является четной, потому что:

$$f(-x) = 4 — (-x)^2 = 4 — x^2 = f(x).$$

Это выполняется для всех $x$, поэтому функция четная.

в) $f(x) = 2 — x$ на промежутке $[0; 3)$ и $T = 3$:

Шаг 1: Анализ функции $f(x) = 2 — x$

Функция $f(x) = 2 — x$ — это линейная функция с коэффициентом $k = -1$, то есть она убывает на всей своей области.

Значение функции:

• Когда $x = 0$, $y = 2 — 0 = 2$.
• Когда $x = 3$, $y = 2 — 3 = -1$.

Шаг 2: Поведение функции на интервале $[0; 3)$

Значения функции:

• $y$ убывает от 2 до $-1$ на интервале $[0; 3)$.

Шаг 3: Периоды функции

Период функции равен $T = 3$, и общие периоды функции можно записать как $T_{\text{общ}} = kT = 3k$.

Шаг 4: График функции

Область определения: $D(f) = (-\infty; +\infty)$.

Множество значений: $E(f) = (-1; 2]$.

Интервал убывания: $f(x)$ убывает на интервале $[3k; 3k + 3)$.

Наибольшее и наименьшее значения:

• $y_{\text{наиб}} = 2$.
• $y_{\text{наим}}$ — нет, так как $y$ убывает без нижней границы.

Нули функции: $f(x) = 0$ при $x = 2$.

Знак функции:

• $f(x) > 0$ на интервале $[3k; 3k + 2)$.
• $f(x) < 0$ на интервале $(3k + 2; 3k + 3)$.

Шаг 5: Четность и нечетность

Функция не является ни четной, ни нечетной, так как:

Для четности $f(-x) = f(x)$ не выполняется.

Для нечетности $f(-x) = -f(x)$ также не выполняется.

г) $f(x) = 2x^2 — 1$ на интервале $(0; 1)$ и $T = 1$:

Шаг 1: Анализ функции $f(x) = 2x^2 — 1$

Функция $f(x) = 2x^2 — 1$ — это парабола, направленная вверх, так как коэффициент при $x^2$ положительный.

Вершина параболы:

• Вершина параболы находится в точке $x_0 = 0$.
• Значение функции в вершине $y_0 = f(0) = -1$.

Шаг 2: Поведение функции на интервале $(0; 1)$

Значения функции:

• Когда $x = 0$, $y = -1$.
• Когда $x = 1$, $y = 1$.

Шаг 3: Периоды функции

Период функции равен $T = 1$, и общие периоды функции можно записать как $T_{\text{общ}} = kT = k$.

Шаг 4: График функции

Область определения: $D(f) = (k; k + 1)$.

Множество значений: $E(f) = (-1; 1)$.

Интервал возрастания: $f(x)$ возрастает на интервале $(k; k + 1)$.

Наибольшее и наименьшее значения:

• $y_{\text{наиб}}$ и $y_{\text{наим}}$ — нет, так как функция имеет асимптоты на бесконечности.

Нули функции: $f(x) = 0$ при $x = k + \frac{1}{\sqrt{2}}$.

Знак функции:

• $f(x) > 0$ на интервале $\left(k + \frac{1}{\sqrt{2}}; k + 1\right)$.
• $f(x) < 0$ на интервале $\left(k; k + \frac{1}{\sqrt{2}}\right)$.

Шаг 5: Четность и нечетность

Функция не является ни четной, ни нечетной.