ГДЗ по Алгебре 10 Класс Номер 9.18 Профильный Уровень Мордкович — Подробные Ответы

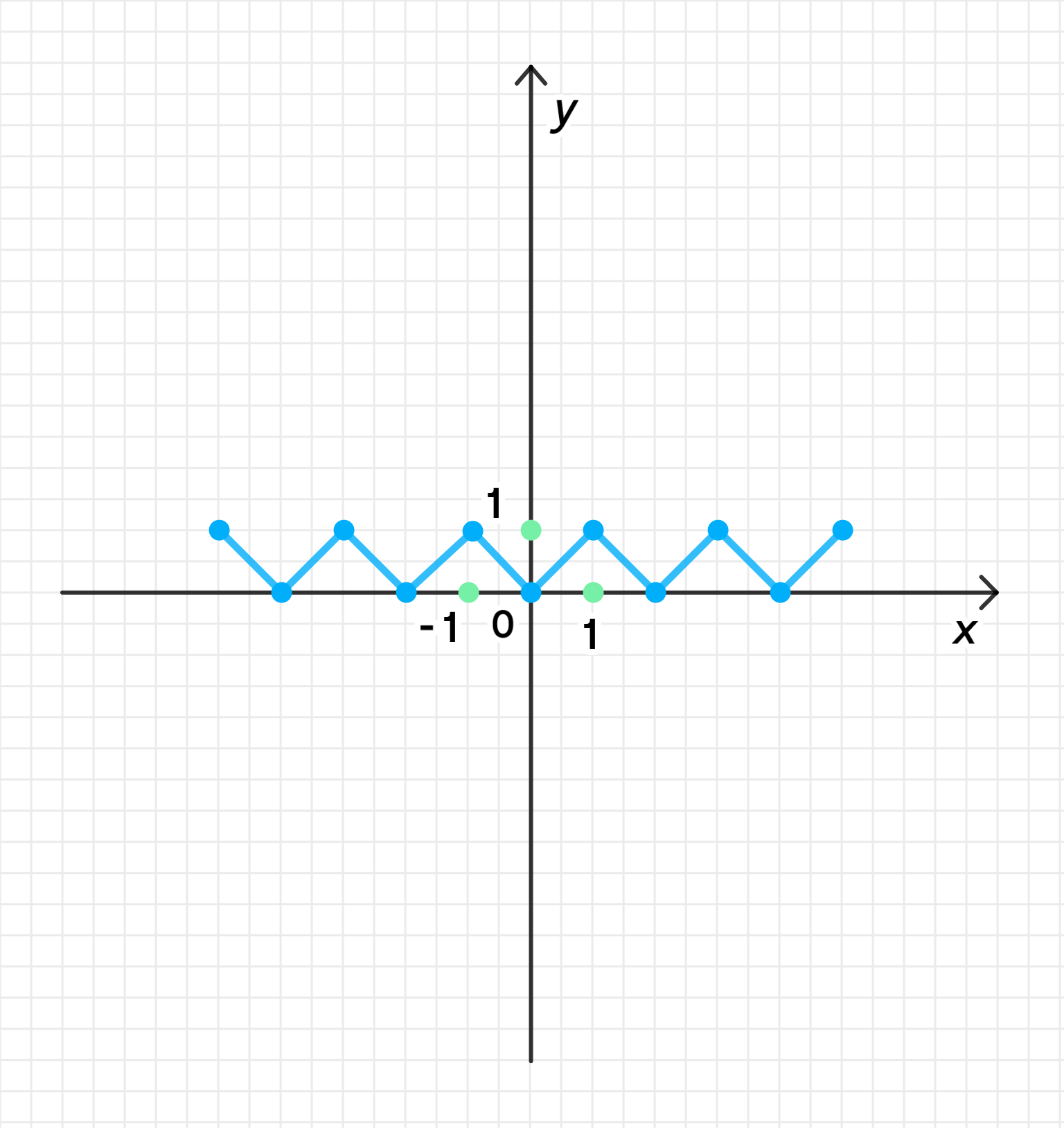
а) Период функции равен 2 и $f(x) = |x|$ на отрезке $[-1; 1]$;

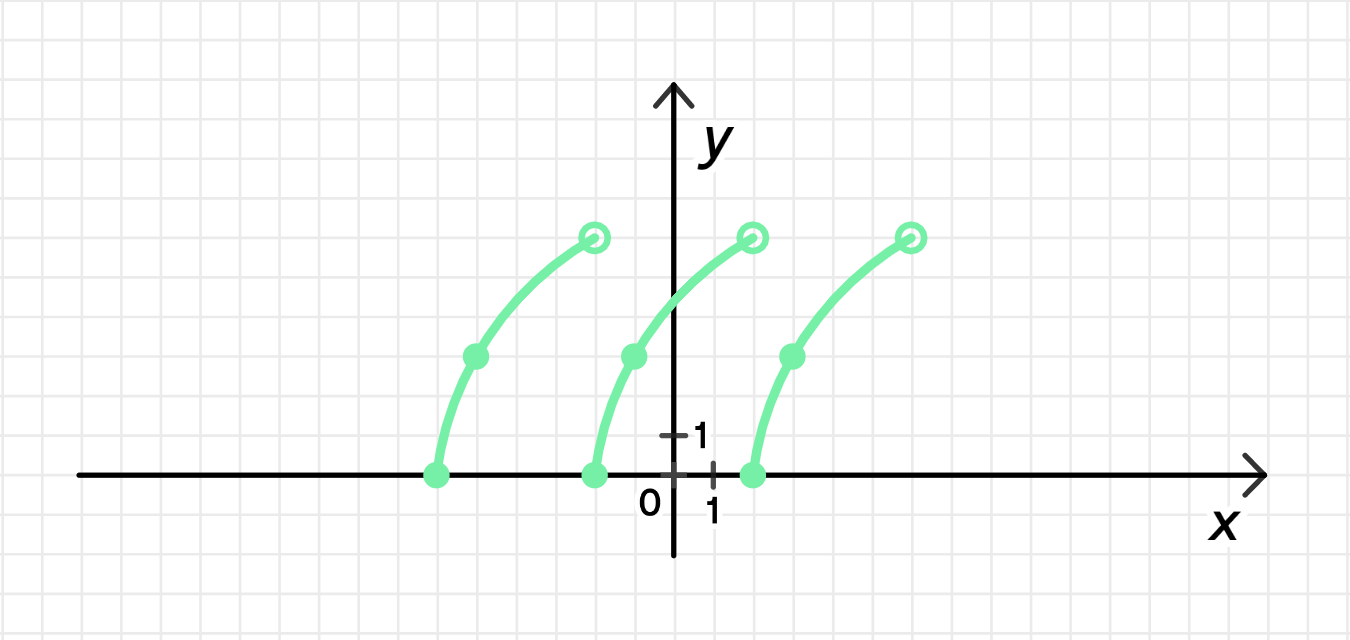
б) Период функции равен 4 и $f(x) = 3\sqrt{x + 2}$ на промежутке $[-2; 2)$;

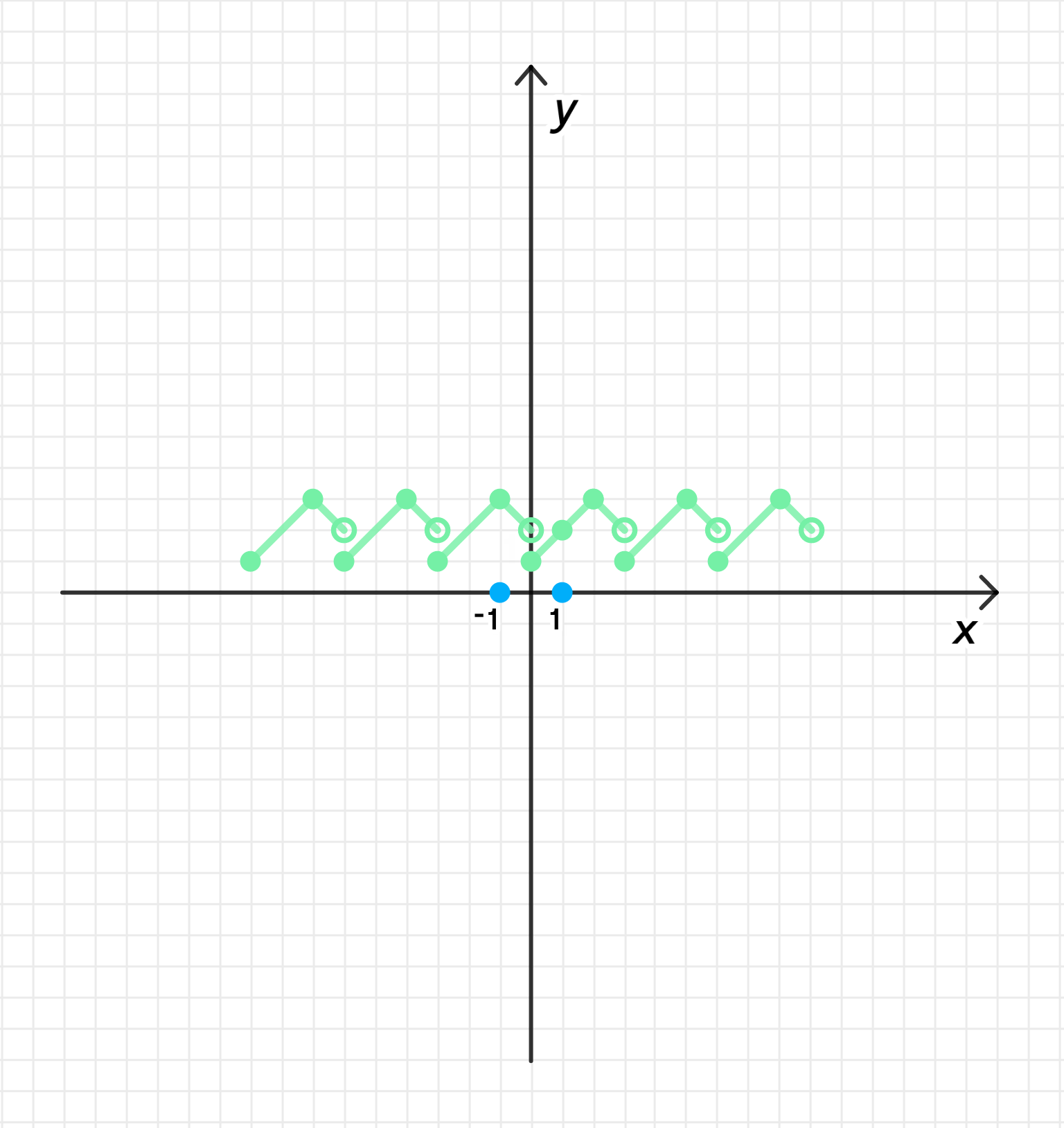
в) Период функции равен 3 и $f(x) = 3 — |2 — x|$ на промежутке $[0; 3)$;

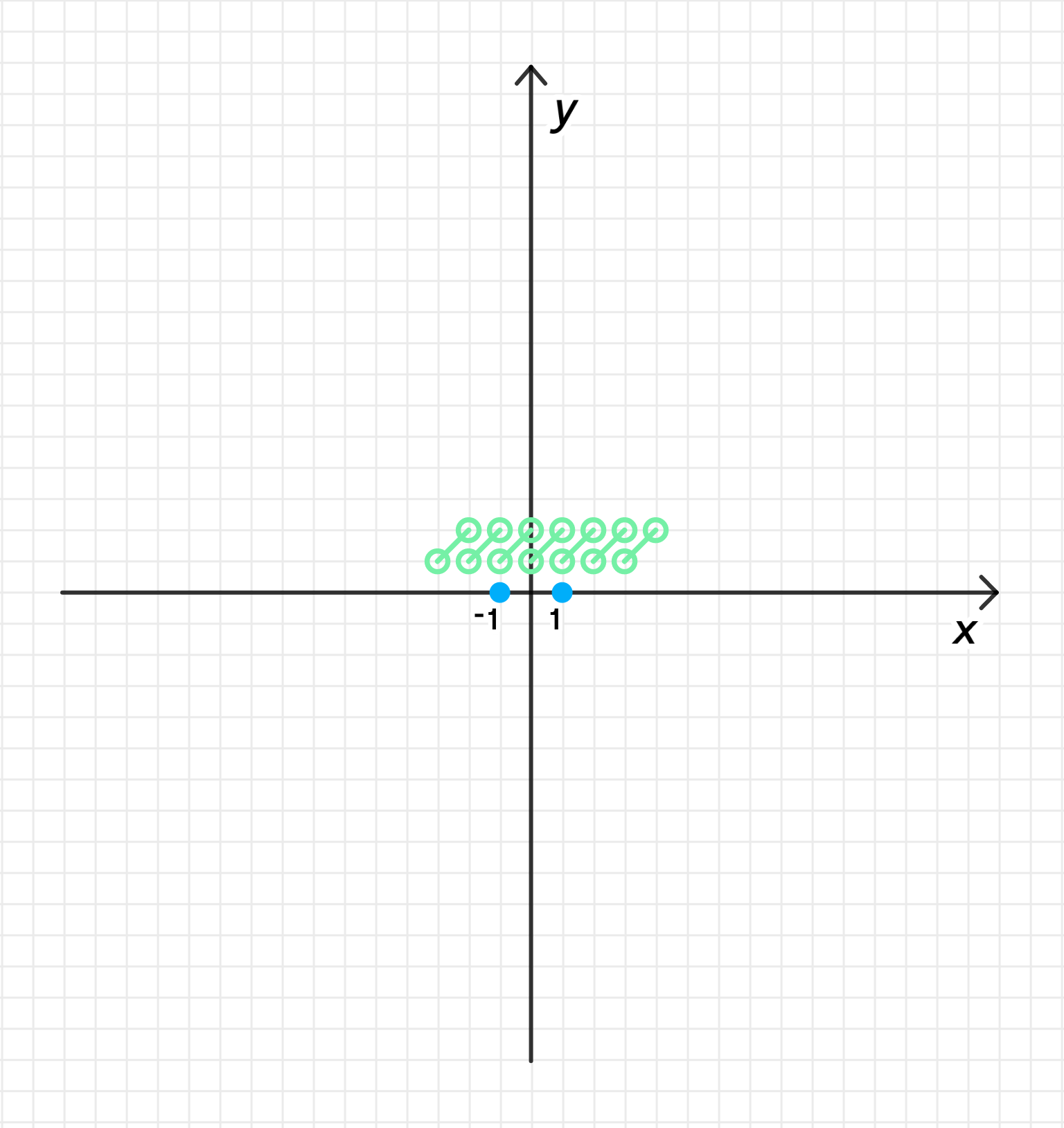
г) Период функции равен 1 и $f(x) = 3 — \sqrt{4 — 3x}$ на промежутке $(0; 1)$.

а) $f(x) = |x|$ на отрезке $[-1; 1]$ и $T = 2$;

Рассмотрим функцию $y = |x|$:

• $k = 1 > 0$ — ветви направлены вверх;
• $a = 1 > 0$;
• $x_0 = 0$ и $y_0 = 0$;
• $|x| = 0 \quad \Rightarrow \quad x = 0$;

Все периоды функции:

• $T_{\text{общ}} = kT = 2k$;

График функции:

• Область определения: $D(f) = (-\infty; +\infty)$;
• Множество значений: $E(f) = [0; 1]$;
• Возрастает на $[2k; 2k + 1]$ и убывает на $[2k — 1; 2k]$;
• Наибольшее и наименьшее значения:
  • $y_{\text{наиб}} = 1$ и $y_{\text{наим}} = 0$;
• Нули функции: $x = 2k$;
• $f(x) > 0$ на $(2k; 2k + 2)$;
• Функция является четной;

б) $f(x) = 3\sqrt{x + 2}$ на промежутке $[-2; 2]$ и $T = 4$;

Рассмотрим функцию $y = 3\sqrt{x + 2}$:

• $k = 1 > 0$;
• $a = 1 > 0$ — функция возрастает;
• $x_0 = -2$ и $y_0 = 0$;
• $3\sqrt{x + 2} = 0 \quad \Rightarrow \quad x + 2 = 0 \quad \Rightarrow \quad x = -2$;

Все периоды функции:

• $T_{\text{общ}} = kT = 4k$;

График функции:

• Область определения: $D(f) = (-\infty; +\infty)$;
• Множество значений: $E(f) = [0; 6]$;
• Возрастает на $[4k — 2; 4k + 2)$;
• Наибольшее и наименьшее значения:
  • $y_{\text{наиб}}$ нет и $y_{\text{наим}} = 0$;
• Нули функции: $x = 4k — 2$;
• $f(x) > 0$ на $(4k — 2; 4k + 2)$;
• Функция ни четная, ни нечетная;

в) $f(x) = 3 — |2 — x|$ на промежутке $[0; 3]$ и $T = 3$;

Рассмотрим функцию $y = 3 — |2 — x|$:

• $k = -1 < 0$;
• $a = -1 < 0$ — ветви направлены вверх;
• $x_0 = 2$ и $y_0 = 3$;
• $3 — |2 — x| = 0 \quad \Rightarrow \quad 2 — x = \pm 3 \quad \Rightarrow \quad \begin{cases} x_1 = -1 \\ x_2 = 5 \end{cases}$;

Все периоды функции:

• $T_{\text{общ}} = kT = 3k$;

График функции:

• Область определения: $D(f) = (-\infty; +\infty)$;
• Множество значений: $E(f) = [1; 3]$;
• Возрастает на $[3k; 3k + 2]$ и убывает на $[3k + 2; 3k + 3]$;
• Наибольшее и наименьшее значения:
  • $y_{\text{наиб}} = 3$ и $y_{\text{наим}} = 1$;
• Нули функции отсутствуют;
• $f(x) > 0$ на $(-∞; +∞)$;
• Функция ни четная, ни нечетная;

г) $f(x) = 3 — \sqrt{4 — 3x}$ на промежутке $(0; 1)$ и $T = 1$;

Рассмотрим функцию $y = 3 — \sqrt{4 — 3x}$:

• $k = -1 < 0$;
• $a = -1 < 0$ — функция возрастает;
• $x_0 = \frac{1}{3}$ и $y_0 = 3$;
• $3 — \sqrt{4 — 3x} = 0 \quad \Rightarrow \quad 4 — 3x = 9 \quad \Rightarrow \quad x = -1 \frac{2}{3}$;

Все периоды функции:

• $T_{\text{общ}} = kT = k$;

График функции:

• Область определения: $D(f) = (k; k + 1)$;
• Множество значений: $E(f) = (1; 2)$;
• Возрастает на $(k; k + 1)$;
• Наибольшее и наименьшее значения:
  • $y_{\text{наиб}}$ нет и $y_{\text{наим}}$ нет;
• Нули функции отсутствуют;
• $f(x) > 0$ на $(k; k + 1)$;
• Функция ни четная, ни нечетная

а) $f(x) = |x|$ на отрезке $[-1; 1]$ и $T = 2$:

Шаг 1: Определение функции и ее поведения

Функция $f(x) = |x|$ — это абсолютное значение, которая имеет характерный график в виде «V», открывающийся вверх.

Константа $k$:

• Функция $f(x) = |x|$ является симметричной относительно оси $y$ и возрастает для $x > 0$, убывает для $x < 0$. В данном случае $k = 1$, так как коэффициент при $x$ в выражении абсолютной величины равен 1.

Вершина графика:

• Вершина функции — это точка, где функция достигает минимального значения. Для функции $f(x) = |x|$, эта точка будет $x_0 = 0$, а значение функции в этой точке $y_0 = 0$.

Значения функции:

• При $x = -1$, $f(x) = 1$.
• При $x = 1$, $f(x) = 1$.

Таблица значений функции:

$$\begin{array}{|c|c|c|} \hline x & -1 & 1 \\ \hline f(x) & 1 & 1 \\ \hline \end{array}$$

Шаг 2: Периоды функции

Периодичность функции заключается в том, что абсолютное значение функции $|x|$ повторяется через каждый интервал длины 2. Таким образом, период функции на данном интервале равен $T = 2$.

Все периоды функции:

$$T_{\text{общ}} = kT = 2k,$$

где $k$ — целое число. Период функции будет повторяться каждые 2 единицы на всей числовой оси.

Шаг 3: График функции

Область определения: $D(f) = (-\infty; +\infty)$, так как функция абсолютного значения определена для всех $x$.

Множество значений: $E(f) = [0; 1]$, так как на отрезке $[-1; 1]$ функция принимает значения от 0 до 1.

Интервалы возрастания и убывания:

• Функция возрастает на интервале $[0; 1]$ и убывает на интервале $[-1; 0]$.

Наибольшее и наименьшее значения:

• Наибольшее значение функции на отрезке $[-1; 1]$: $y_{\text{наиб}} = 1$, которое достигается в точках $x = -1$ и $x = 1$.
• Наименьшее значение функции: $y_{\text{наим}} = 0$, которое достигается в точке $x = 0$.

Нули функции:

• Функция обнуляется в точке $x = 0$.

Знак функции:

• $f(x) > 0$ на интервале $(0; 1]$.
• $f(x) < 0$ на интервале $[-1; 0)$.

Шаг 4: Четность функции

Функция является четной, так как:

$$f(-x) = | -x | = |x| = f(x),$$

что выполняется для всех значений $x$.

б) $f(x) = 3\sqrt{x + 2}$ на промежутке $[-2; 2]$ и $T = 4$:

Шаг 1: Определение функции и ее поведения

Функция $f(x) = 3\sqrt{x + 2}$ является корнем с положительным коэффициентом, и функция возрастает на интервале $[-2; 2]$.

Константа $k$:

• $k = 3$, так как перед корнем стоит множитель 3.

Вершина графика:

• Функция будет возрастать с минимального значения в точке $x_0 = -2$, где $f(-2) = 0$.

Значения функции:

• Когда $x = -2$, $f(x) = 0$.
• Когда $x = -1$, $f(x) = 3\sqrt{-1 + 2} = 3$.
• Когда $x = 2$, $f(x) = 3\sqrt{2 + 2} = 6$.

Таблица значений функции:

$$\begin{array}{|c|c|c|c|} \hline x & -2 & -1 & 2 \\ \hline f(x) & 0 & 3 & 6 \\ \hline \end{array}$$

Шаг 2: Периоды функции

Период функции равен $T = 4$, и общие периоды функции могут быть записаны как $T_{\text{общ}} = 4k$, где $k$ — целое число.

Шаг 3: График функции

Область определения: $D(f) = [-2; 2]$, так как подкоренное выражение $x + 2$ должно быть неотрицательным.

Множество значений: $E(f) = [0; 6]$, так как функция принимает значения от 0 до 6.

Интервал возрастания:

• Функция возрастает на интервале $[-2; 2]$.

Наибольшее и наименьшее значения:

• Наибольшее значение $y_{\text{наиб}} = 6$, которое достигается при $x = 2$.
• Наименьшее значение $y_{\text{наим}} = 0$, которое достигается при $x = -2$.

Нули функции:

• Функция обнуляется в точке $x = -2$.

Знак функции:

• Функция всегда положительна на интервале $[-2; 2]$, так как $f(x) = 3\sqrt{x + 2} \geq 0$.

Шаг 4: Четность функции

Функция не является четной, так как:

$$f(-x) = 3\sqrt{-x + 2} \neq f(x).$$

Она также не является нечетной, так как не выполняется условие $f(-x) = -f(x)$.

в) $f(x) = 3 — |2 — x|$ на промежутке $[0; 3]$ и $T = 3$:

Шаг 1: Определение функции и ее поведения

Функция $f(x) = 3 — |2 — x|$ имеет вид, который указывает на симметричную функцию относительно точки $x = 2$.

Константа $k$:

• $k = -1$, так как функция имеет отрицательное значение перед абсолютным значением.

Вершина графика:

• Вершина функции $f(x) = 3 — |2 — x|$ будет достигаться при $x_0 = 2$, где функция достигает максимального значения $y_0 = 3$.

Значения функции:

• При $x = 0$, $f(x) = 3 — |2 — 0| = 3 — 2 = 1$.
• При $x = 1$, $f(x) = 3 — |2 — 1| = 3 — 1 = 2$.
• При $x = 3$, $f(x) = 3 — |2 — 3| = 3 — 1 = 2$.

Таблица значений функции:

$$\begin{array}{|c|c|c|c|} \hline x & 0 & 1 & 3 \\ \hline f(x) & 1 & 2 & 2 \\ \hline \end{array}$$

Шаг 2: Периоды функции

Период функции равен $T = 3$, и все возможные периоды могут быть записаны как $T_{\text{общ}} = 3k$.

Шаг 3: График функции

Область определения: $D(f) = [0; 3]$.

Множество значений: $E(f) = [1; 3]$.

Интервалы возрастания и убывания:

• Функция возрастает на интервале $[0; 2]$.
• Функция убывает на интервале $[2; 3]$.

Наибольшее и наименьшее значения:

• Наибольшее значение $y_{\text{наиб}} = 3$ в точке $x = 2$.
• Наименьшее значение $y_{\text{наим}} = 1$ в точке $x = 0$.

Нули функции: Нули функции отсутствуют, так как $f(x) \geq 0$ на всей области определения.

Шаг 4: Четность функции

Функция не является ни четной, ни нечетной, так как не удовлетворяет ни одному из условий для четности или нечетности.

г) $f(x) = 3 — \sqrt{4 — 3x}$ на промежутке $(0; 1)$ и $T = 1$:

Шаг 1: Определение функции и ее поведения

Функция $f(x) = 3 — \sqrt{4 — 3x}$ представляет собой квадратный корень, и для $x \in (0; 1)$ она будет возрастать.

Константа $k$:

• $k = -1$, так как перед квадратным корнем стоит отрицательная константа.

Вершина графика:

• Вершина будет в точке $x_0 = \frac{1}{3}$, где функция достигает минимального значения.

Значения функции:

• При $x = 0$, $f(x) = 3 — \sqrt{4} = 1$.
• При $x = 1$, $f(x) = 3 — \sqrt{1} = 2$.

Таблица значений функции:

$$\begin{array}{|c|c|c|} \hline x & 0 & 1 \\ \hline f(x) & 1 & 2 \\ \hline \end{array}$$

Шаг 2: Периоды функции

Период функции равен $T = 1$, и все возможные периоды могут быть записаны как $T_{\text{общ}} = k$.

Шаг 3: График функции

Область определения: $D(f) = \left(0; 1\right)$.

Множество значений: $E(f) = (1; 2)$.

Интервалы возрастания:

• Функция возрастает на интервале $(0; 1)$.

Наибольшее и наименьшее значения:

• $y_{\text{наиб}}$ и $y_{\text{наим}}$ отсутствуют, так как функция не достигает экстремумов.

Нули функции: Нули функции отсутствуют, так как функция всегда положительна.

Шаг 4: Четность функции

Функция не является ни четной, ни нечетной.