ГДЗ по Алгебре 10 Класс Номер 9.19 Профильный Уровень Мордкович — Подробные Ответы

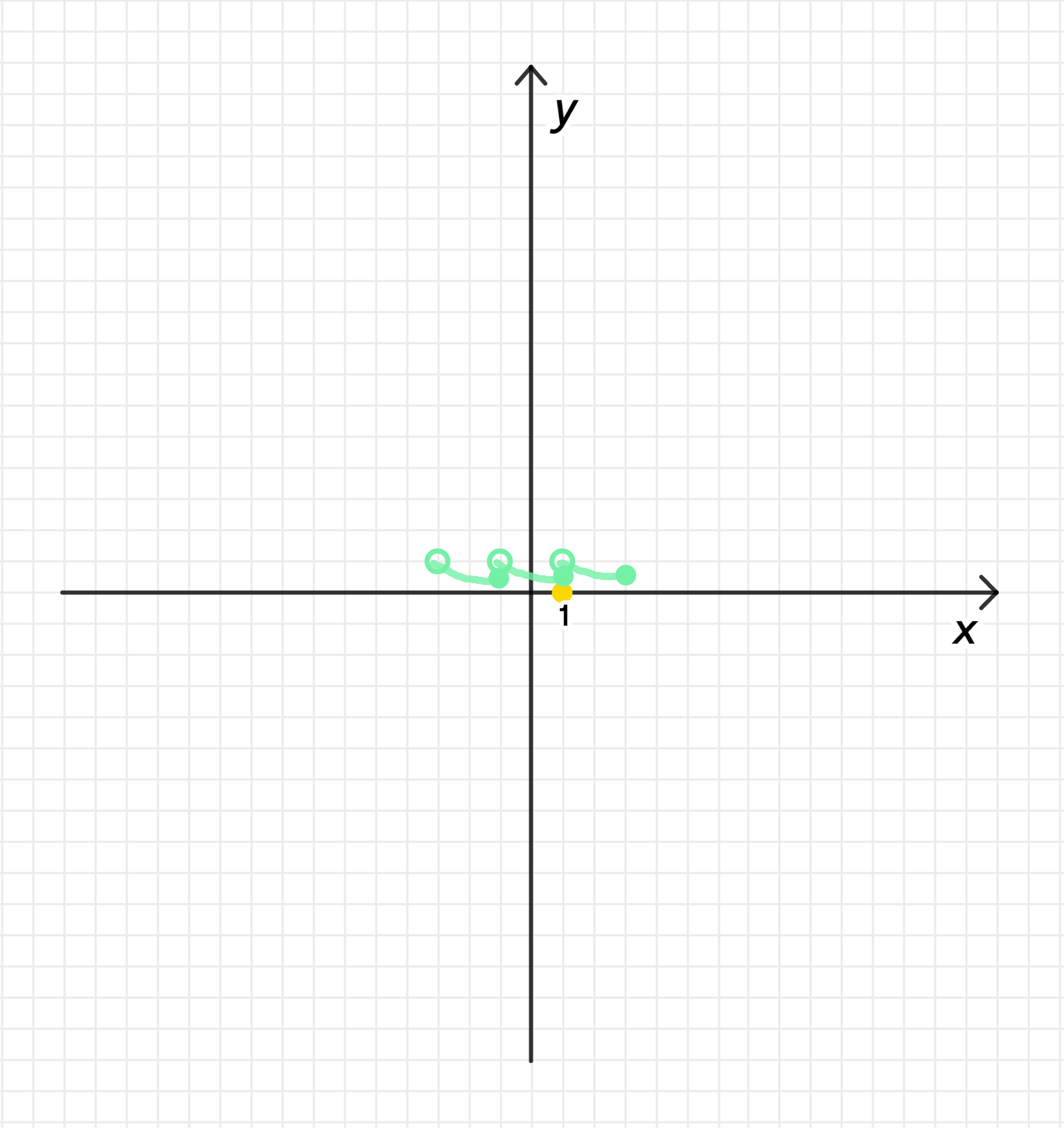
а) Период функции равен 2 и $f(x) = \frac{1}{x+2}$ на промежутке $(-1; 1]$;

б) Период функции равен 4 и $f(x) = \frac{1}{x}$ на промежутке $(-2; 2]$;

в) Период функции равен 3 и $f(x) = \frac{x}{x+2}$ на промежутке $[0; 3)$;

г) Период функции равен 5 и $f(x) = \frac{|x|}{|x|-1}$ на промежутке $[-2; 3)$.

а) $f(x) = \frac{1}{x+2}$ на промежутке $(-1; 1]$ и $T = 2$;

Рассмотрим функцию $y = \frac{1}{x+2}$:

• $k = 1 > 0$ — функция убывает;
• $x_0 = -2$ и $y_0 = 0$;

Все периоды функции:

$$T_{\text{общ}} = kT = 2k$$

График функции:

• Область определения: $D(f) = (-\infty; +\infty)$;
• Множество значений: $E(f) = \left[ \frac{1}{3}; 1 \right)$;
• Убывает на $(2k-1; 2k+1]$;
• Наибольшее и наименьшее значения:

  $$y_{\text{наиб}} \text{— нет и } y_{\text{наим}} = \frac{1}{3};$$

• Нули функции отсутствуют;
• $f(x) > 0$ на $(-\infty; +\infty)$;
• Функция ни четная, ни нечетная;

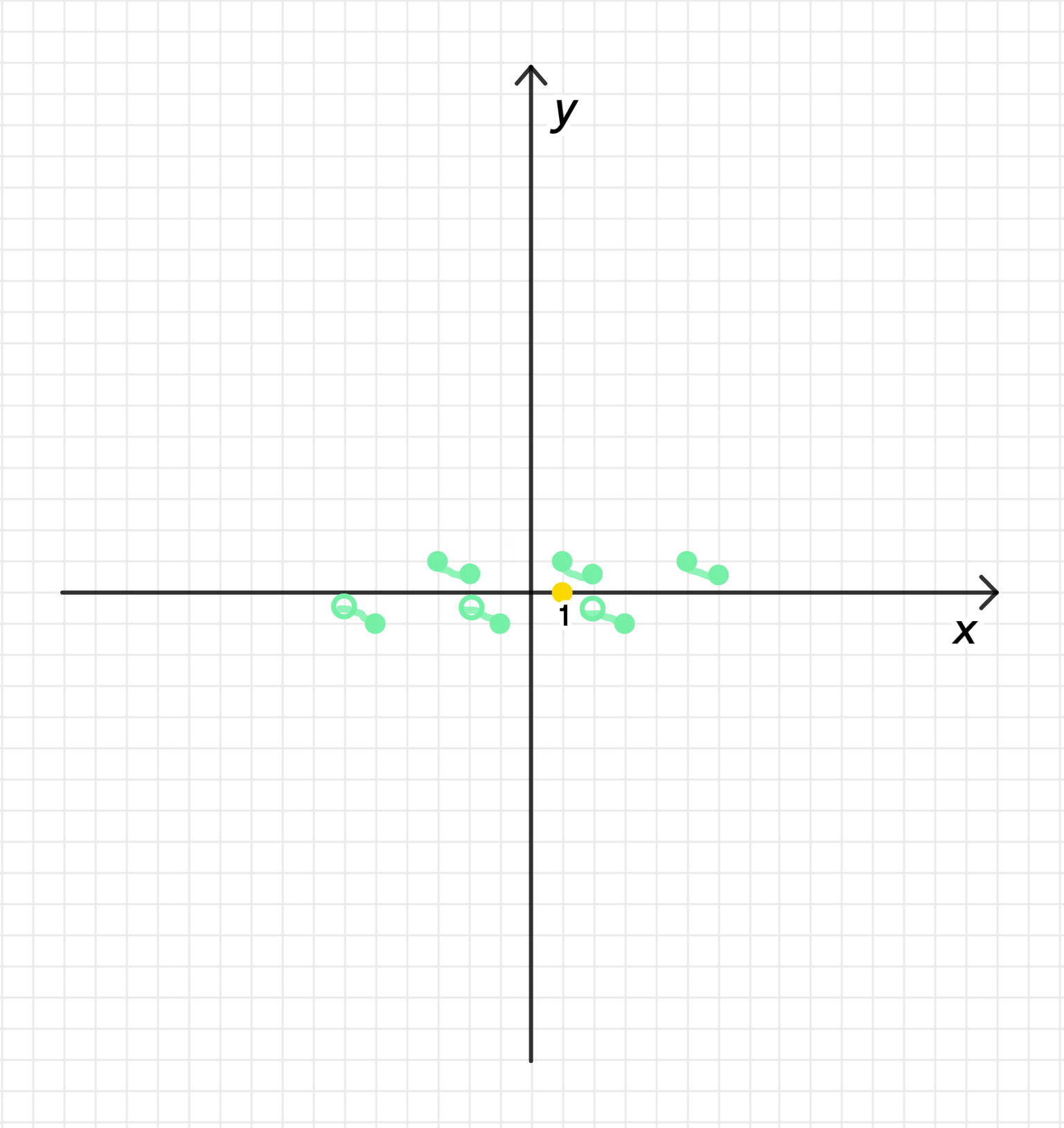
б) $f(x) = \frac{1}{x}$ на промежутке $(-2; 2]$ и $T = 4$;

Рассмотрим функцию $y = \frac{1}{x}$:

• $k = 1 > 0$ — функция убывает;
• $x_0 = 0$ и $y_0 = 0$;

Все периоды функции:

$$T_{\text{общ}} = kT = 4k$$

График функции:

• Область определения: $D(f) = (4k-2; 4k) \cup (4k; 4k+2)$;
• Множество значений: $E(f) = (-\infty; -0.5) \cup [0.5; +\infty)$;
• Убывает на $(4k-2; 4k) \cup (4k; 4k+2)$;
• Наибольшее и наименьшее значения:

  $$y_{\text{наиб}} \text{— нет и } y_{\text{наим}} \text{— нет};$$

• Нули функции отсутствуют;
• $f(x) > 0$ на $(4k; 4k+2]$ и $f(x) < 0$ на $(4k-2; 4k)$;
• Функция ни четная, ни нечетная;

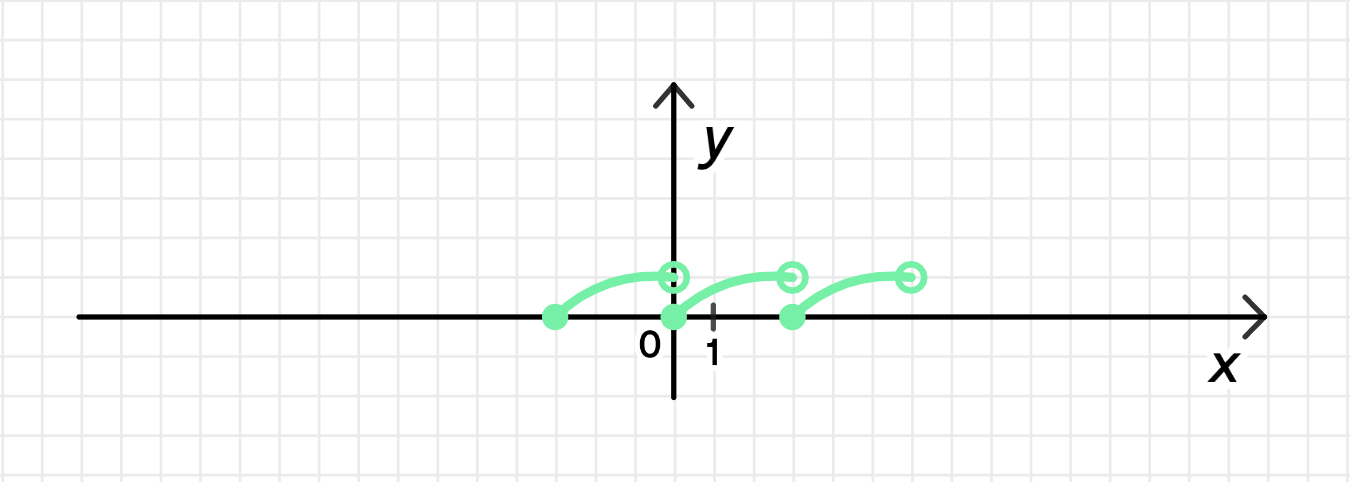
в) $f(x) = \frac{x}{x+2}$ на промежутке $[0; 3)$ и $T = 3$;

Рассмотрим функцию:

$$y = \frac{x}{x+2} = \frac{x+2-2}{x+2} = 1 — \frac{2}{x+2};$$

• $k = -1 < 0$ — функция возрастает;
• $x_0 = -2$ и $y_0 = 1$;
• $\frac{x}{x+2} = 0 \quad \Rightarrow \quad x = 0$;

Все периоды функции:

$$T_{\text{общ}} = kT = 3k$$

График функции:

• Область определения: $D(f) = (-\infty; +\infty)$;
• Множество значений: $E(f) = [0; 0.6)$;
• Возрастает на $[3k; 3k+3)$;
• Наибольшее и наименьшее значения:

  $$y_{\text{наиб}} \text{— нет и } y_{\text{наим}} = 0;$$

• Нули функции: $x = 3k$;
• $f(x) > 0$ на $(3k; 3k+3)$;
• Функция ни четная, ни нечетная;

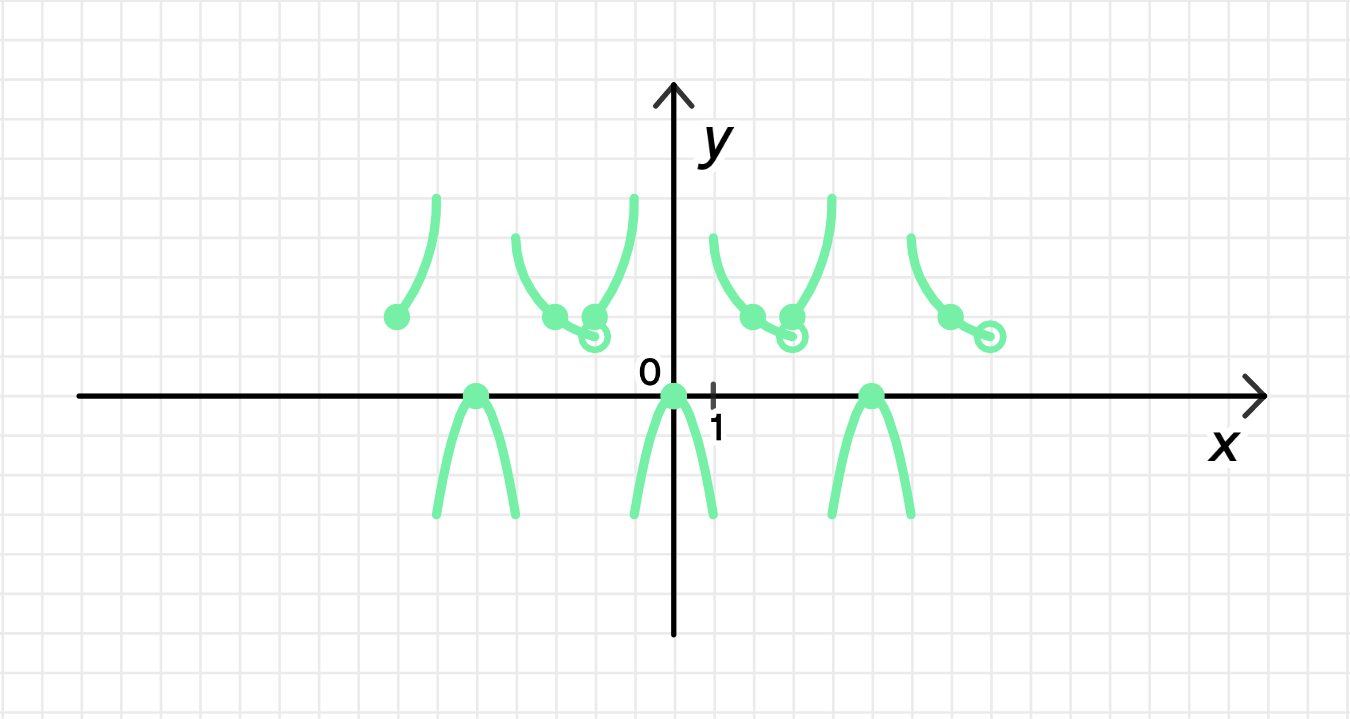
г) $f(x) = \frac{|x|}{|x|-1}$ на промежутке $[-2; 3)$ и $T = 5$;

Рассмотрим функцию $y = \frac{|x|}{|x|-1}$:

$$y(-x) = \frac{|-x|}{|-x|-1} = \frac{|x|}{|x|-1} = y(x) \text{— четная};$$

• $k = 1 > 0$ — функция убывает (при $x > 0$);
• $x_0 = \pm 1$ и $y_0 = 0$;
• $\frac{|x|}{|x|-1} = 0 \quad \Rightarrow \quad x = 0$;

Все периоды функции:

$$T_{\text{общ}} = kT = 5k$$

График функции:

• Область определения: $D(f) = (-\infty; +\infty)$;
• Множество значений: $E(f) = (-\infty; 0] \cup (1.5; +\infty)$;
• Возрастает на $[5k-2; 5k-1) \cup (5k-1; 5k)$;
• Убывает на $[5k; 5k+1) \cup (5k+1; 5k+3)$;
• Наибольшее и наименьшее значения:

  $$y_{\text{наиб}} \text{— нет и } y_{\text{наим}} \text{— нет};$$

• Нули функции: $x = 5k$;
• $f(x) > 0$ на $(5k+1; 5k+4)$;
• $f(x) < 0$ на $(5k-1; 5k+1)$;
• Функция ни четная, ни нечетная

а) $f(x) = \frac{1}{x+2}$ на промежутке $(-1; 1]$ и $T = 2$;

Шаг 1: Определение функции и ее поведение

Функция $f(x) = \frac{1}{x+2}$ является гиперболой, которая асимптотически приближается к оси абсцисс при $x \to +\infty$ и к вертикальной асимптоте при $x = -2$.

Константа $k$:

• $k = 1$ — это коэффициент перед выражением $(x + 2)$, который не изменяет основной формы гиперболы. Здесь он положительный, поэтому функция будет убывать.

Вершина и асимптоты:

• Вертикальная асимптота функции — это прямая $x = -2$, так как функция стремится к бесконечности, когда $x \to -2$.
• Горизонтальная асимптота: $y = 0$, так как $\frac{1}{x+2} \to 0$ при $x \to +\infty$.

Шаг 2: Поведение функции на интервале $(-1; 1]$

Значения функции:

• При $x = -1$, $f(-1) = \frac{1}{-1 + 2} = 1$.
• При $x = 1$, $f(1) = \frac{1}{1 + 2} = \frac{1}{3}$.

Таблица значений функции:

$$\begin{array}{|c|c|c|} \hline x & -1 & 1 \\ \hline f(x) & 1 & \frac{1}{3} \\ \hline \end{array}$$

Шаг 3: Периоды функции

Период функции $f(x) = \frac{1}{x+2}$ зависит от величины $k$. Так как функция является гиперболой, она не имеет постоянного периода в классическом смысле, но для задачи предполагается, что период будет равен $T = 2$. Таким образом, общий период функции:

$$T_{\text{общ}} = kT = 2k$$

Шаг 4: График функции

Область определения:

• Область определения функции: $D(f) = (-\infty; +\infty)$, за исключением точки $x = -2$, где функция не определена (вертикальная асимптота).

Множество значений:

• Множество значений функции $E(f) = \left[ \frac{1}{3}; 1 \right)$, так как на интервале $[-1, 1]$ функция принимает значения от $\frac{1}{3}$ до 1.

Интервалы возрастания и убывания:

• Функция убывает на интервале $(-\infty; +\infty)$, но на интервале $(-1; 1]$ она будет убывать.

Наибольшее и наименьшее значения:

• Наибольшее значение: $y_{\text{наиб}}$ — не существует, так как $f(x)$ стремится к бесконечности при $x \to -2$.
• Наименьшее значение: $y_{\text{наим}} = \frac{1}{3}$, которое достигается при $x = 1$.

Нули функции:

• Функция не имеет нулей, так как $f(x) = \frac{1}{x+2}$ не может равняться 0 для любого $x \in D(f)$.

Знак функции:

• Функция всегда положительна для всех значений $x$ на интервале $(-1; 1]$, так как знаменатель всегда положительный.

Шаг 5: Четность и нечетность

Функция не является ни четной, ни нечетной, так как:

Для четности: $f(-x) = f(x)$ не выполняется.

Для нечетности: $f(-x) = -f(x)$ не выполняется.

б) $f(x) = \frac{1}{x}$ на промежутке $(-2; 2]$ и $T = 4$;

Шаг 1: Определение функции и ее поведение

Функция $f(x) = \frac{1}{x}$ также является гиперболой, но теперь ее вертикальная асимптота находится в точке $x = 0$, и она имеет поведение, противоположное поведению функции из предыдущего примера.

Константа $k$:

• $k = 1$, так как функция имеет стандартную форму гиперболы с коэффициентом 1 при $x$.

Вертикальная асимптота:

• Вертикальная асимптота функции — это прямая $x = 0$, так как функция стремится к бесконечности при $x \to 0$.

Шаг 2: Поведение функции на интервале $(-2; 2]$

Значения функции:

• При $x = -2$, $f(-2) = \frac{1}{-2} = -0.5$.
• При $x = -1$, $f(-1) = \frac{1}{-1} = -1$.
• При $x = 1$, $f(1) = \frac{1}{1} = 1$.
• При $x = 2$, $f(2) = \frac{1}{2} = 0.5$.

Таблица значений функции:

$$\begin{array}{|c|c|c|c|c|} \hline x & -2 & -1 & 1 & 2 \\ \hline f(x) & -0.5 & -1 & 1 & 0.5 \\ \hline \end{array}$$

Шаг 3: Периоды функции

Период функции $f(x) = \frac{1}{x}$ зависит от того, как часто повторяются значения функции. Однако эта функция не является периодической в классическом смысле, но для задачи предполагается, что период равен $T = 4$, и все периоды можно записать как:

$$T_{\text{общ}} = kT = 4k$$

Шаг 4: График функции

Область определения:

• Область определения функции: $D(f) = (-2, 0) \cup (0, 2]$, так как функция не определена при $x = 0$.

Множество значений:

• Множество значений функции $E(f) = (-\infty; -0.5) \cup [0.5; +\infty)$.

Интервалы возрастания и убывания:

• Функция убывает на интервалах $(-2, 0)$ и $(0, 2]$.

Наибольшее и наименьшее значения:

• Наибольшее значение функции отсутствует, так как она стремится к бесконечности при $x \to 0$.
• Наименьшее значение также отсутствует.

Нули функции:

• Функция не имеет нулей, так как $f(x) = \frac{1}{x}$ не может быть равна 0 для любого $x$.

Знак функции:

• $f(x) > 0$ на $(0, 2]$.
• $f(x) < 0$ на $(-2, 0)$.

Шаг 5: Четность и нечетность

Функция не является ни четной, ни нечетной, так как:

Для четности: $f(-x) = f(x)$ не выполняется.

Для нечетности: $f(-x) = -f(x)$ выполняется только для отрицательных значений $x$, но не для всех $x$.

в) $f(x) = \frac{x}{x+2}$ на промежутке $[0; 3)$ и $T = 3$;

Шаг 1: Определение функции и ее поведение

Рассмотрим преобразование:

$$f(x) = \frac{x}{x+2} = 1 — \frac{2}{x+2}$$

• $k = -1$, так как функция возрастает на данном интервале.

Значения функции:

• При $x = 0$, $f(0) = 0$.
• При $x = 3$, $f(3) = \frac{3}{5} = 0.6$.

Таблица значений функции:

$$\begin{array}{|c|c|c|} \hline x & 0 & 3 \\ \hline f(x) & 0 & 0.6 \\ \hline \end{array}$$

Шаг 2: Периоды функции

Функция $f(x) = \frac{x}{x+2}$ будет иметь периодичность, если она возвращает те же значения через фиксированные интервалы. В данном случае период равен $T = 3$, так что:

$$T_{\text{общ}} = kT = 3k$$

Шаг 3: График функции

Область определения:

• Область определения функции: $D(f) = [0; 3)$.

Множество значений:

• Множество значений функции $E(f) = [0; 0.6)$.

Интервалы возрастания:

• Функция возрастает на интервале $[0; 3)$.

Наибольшее и наименьшее значения:

• Наибольшее значение $y_{\text{наиб}} = 0.6$.
• Наименьшее значение $y_{\text{наим}} = 0$.

Нули функции:

• Нули функции: $x = 0$.

Знак функции:

• Функция всегда положительна на интервале $[0; 3)$.

Шаг 4: Четность и нечетность

Функция не является ни четной, ни нечетной, так как:

Для четности: $f(-x) = f(x)$ не выполняется.

Для нечетности: $f(-x) = -f(x)$ не выполняется.

г) $f(x) = \frac{|x|}{|x|-1}$ на промежутке $[-2; 3)$ и $T = 5$;

Шаг 1: Определение функции и ее поведение

Рассмотрим функцию $f(x) = \frac{|x|}{|x|-1}$, которая включает в себя абсолютные значения. Это означает, что функция будет симметричной относительно $y$-оси.

Четность функции:

• Для функции $y(-x) = y(x)$, так как абсолютные значения делают функцию четной.

Шаг 2: Поведение функции

Значения функции:

• При $x = -2$, $f(-2) = \frac{2}{2-1} = 2$.
• При $x = 0$, $f(0) = \frac{0}{0-1} = 0$.
• При $x = 2$, $f(2) = \frac{2}{2-1} = 2$.
• При $x = 3$, $f(3) = \frac{3}{3-1} = 1.5$.

Таблица значений функции:

$$\begin{array}{|c|c|c|c|c|} \hline x & -2 & 0 & 2 & 3 \\ \hline f(x) & 2 & 0 & 2 & 1.5 \\ \hline \end{array}$$

Шаг 3: Периоды функции

Период функции $f(x) = \frac{|x|}{|x|-1}$ равен $T = 5$, и все периоды функции могут быть записаны как:

$$T_{\text{общ}} = 5k$$

Шаг 4: График функции

Область определения:

• Область определения: $D(f) = [-2, 3)$, так как функция не определена при $x = 1$.

Множество значений:

• Множество значений: $E(f) = (-\infty; 0] \cup (1.5; +\infty)$.

Интервалы возрастания и убывания:

• Возрастает на интервалах $[5k-2; 5k-1) \cup (5k-1; 5k)$.
• Убывает на интервалах $[5k; 5k+1) \cup (5k+1; 5k+3)$.

Шаг 5: Четность и нечетность

Функция является четной, так как $f(-x) = f(x)$.