ГДЗ по Алгебре 10 Класс Номер 9.29 Профильный Уровень Мордкович — Подробные Ответы

Постройте график функции и определите, является ли функция периодической:

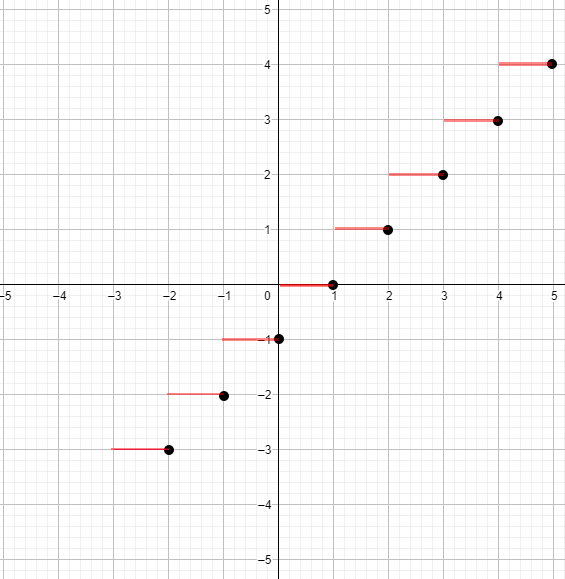
а) у = [x];

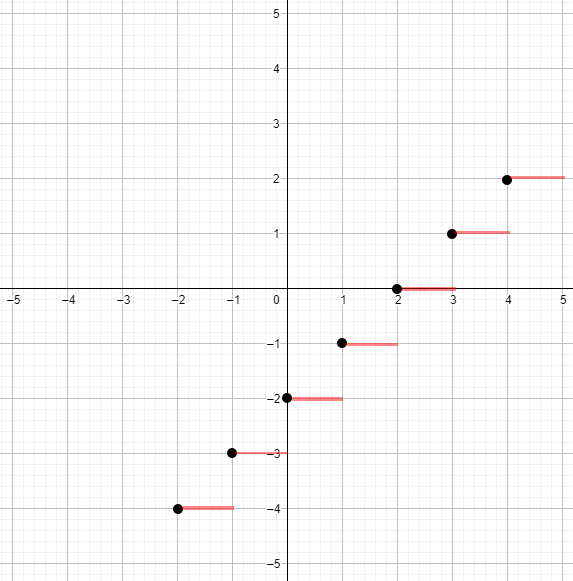
б) у = [x — 2,5];

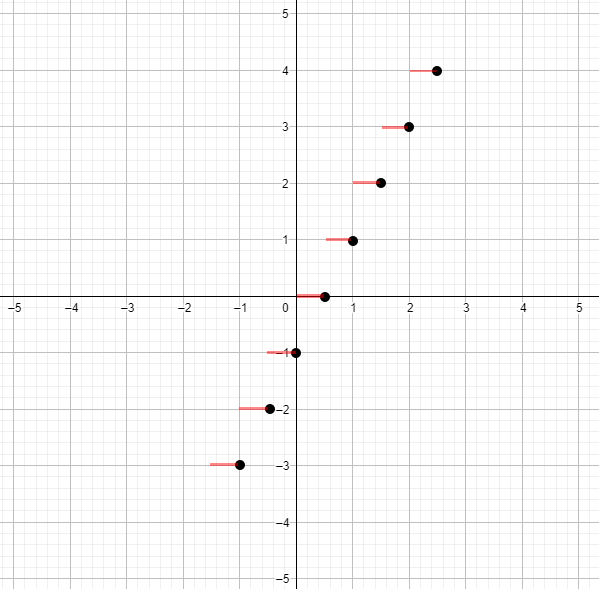
в) у = [2x];

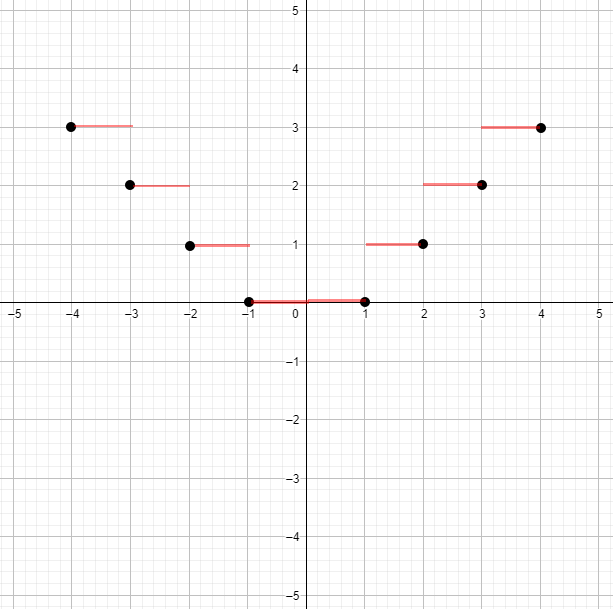
г) у = [|х|].

а) $y = [x]$;

Решение равенства:

$$y = [x] = k;$$ $$k \leq x < k + 1;$$

График функции:

Ответ: не является.

б) $y = [x — 2.5]$;

Решение равенства:

$$y = [x — 2.5] = k;$$ $$k \leq x — 2.5 < k + 1;$$ $$k + 2.5 \leq x < k + 3.5;$$

График функции:

Ответ: не является.

в) $y = [2x]$;

Решение равенства:

$$y = [2x] = k;$$ $$k \leq 2x < k + 1;$$ $$\frac{k}{2} \leq x < \frac{k + 1}{2};$$

График функции:

Ответ: не является.

г) $y = [|x|]$;

Функция является четной:

$$y(-x) = [|{-x}|] = [|x|] = y(x);$$

Если $x > 0$, тогда:

$$y = [x] = k;$$ $$k \leq x < k + 1;$$

График функции:

Ответ: не является.

а) $y = [x]$

Решение равенства:

Дано:

$$y = [x] = k,$$

где $k \in \mathbb{Z}$ — целая часть числа $x$.

По определению целой части числа, $[x]$ — это наибольшее целое число, не превышающее $x$. То есть, целая часть числа $x$ находится в интервале:

$$k \leq x < k + 1,$$

где $k$ — целая часть числа $x$.

Таким образом, решение равенства $y = [x] = k$ сводится к тому, что $k$ — это целая часть числа $x$, и для каждого $k$ существует интервал $k \leq x < k + 1$, в котором выполняется равенство.

График функции $y = [x]$:

График функции $y = [x]$ представляет собой ступенчатую линию, где каждый «степ» начинается с целого числа $k$ и заканчивается перед следующим целым числом $k + 1$. Это означает, что для всех $x$, лежащих в интервале $k \leq x < k + 1$, функция $y = [x]$ будет равна $k$. График имеет горизонтальные участки, и происходит скачок каждый раз, когда $x$ достигает нового целого числа.

Ответ: График не является функцией, так как она не является непрерывной. Функция является разрывной на каждом целочисленном значении $x$, поэтому такой график нельзя назвать гладким.

б) $y = [x — 2.5]$

Решение равенства:

Дано:

$$y = [x — 2.5] = k.$$

Как и в предыдущем случае, $[x — 2.5]$ — это целая часть числа $x — 2.5$. То есть, по определению:

$$k \leq x — 2.5 < k + 1.$$

Теперь, прибавим 2.5 ко всем частям неравенства:

$$k + 2.5 \leq x < k + 3.5.$$

Таким образом, решение равенства сводится к тому, что $x$ должно находиться в интервале от $k + 2.5$ до $k + 3.5$ для любого целого числа $k$.

График функции $y = [x — 2.5]$:

График этой функции также будет ступенчатым, но сдвинутым по оси $x$ на 2.5 единицы влево. Это означает, что график функции будет начинаться в точке $k + 2.5$ и будет продолжаться до $k + 3.5$, где для каждого $k$ функция $y$ будет равна $k$.

Ответ: График функции тоже будет разрывным и ступенчатым, только сдвинутым относительно графика функции $y = [x]$ на 2.5 единицы.

в) $y = [2x]$

Решение равенства:

Дано:

$$y = [2x] = k.$$

Здесь целая часть числа $2x$ равна $k$, что означает:

$$k \leq 2x < k + 1.$$

Теперь разделим обе части неравенства на 2:

$$\frac{k}{2} \leq x < \frac{k + 1}{2}.$$

Таким образом, решение равенства сводится к тому, что для любого целого числа $k$ значение $x$ должно находиться в интервале от $\frac{k}{2}$ до $\frac{k + 1}{2}$.

График функции $y = [2x]$:

График функции $y = [2x]$ также будет ступенчатым, но с более частыми скачками, чем график функции $y = [x]$, потому что каждый «степ» будет происходить на интервале, равном $\frac{1}{2}$, а не 1. Это означает, что при увеличении $x$ скачки будут происходить дважды быстрее.

Ответ: График функции будет ступенчатым и разрывным, с удвоенной частотой скачков по сравнению с графиком функции $y = [x]$.

г) $y = [|x|]$

Функция является четной:

Так как функция $y = [|x|]$ зависит от модуля $|x|$, она является четной. Это означает, что для всех $x$:

$$y(-x) = [|{-x}|] = [|x|] = y(x).$$

Таким образом, график функции симметричен относительно оси $y$.

Рассмотрим случай $x > 0$:

Если $x > 0$, то $|x| = x$, и функция будет вести себя как $y = [x]$, что уже было рассмотрено в предыдущем пункте:

$$y = [x] = k;$$ $$k \leq x < k + 1.$$

Для всех $x$, лежащих в интервале $k \leq x < k + 1$, функция будет равна $k$.

График функции $y = [|x|]$:

График этой функции будет похож на график функции $y = [x]$, но с симметрией относительно оси $y$. То есть, для положительных $x$ график будет точно таким же, как и для отрицательных $x$, поскольку функция зависит от абсолютного значения $x$.

Ответ: График функции будет ступенчатым и разрывным, но симметричным относительно оси $y$, поскольку функция является четной.