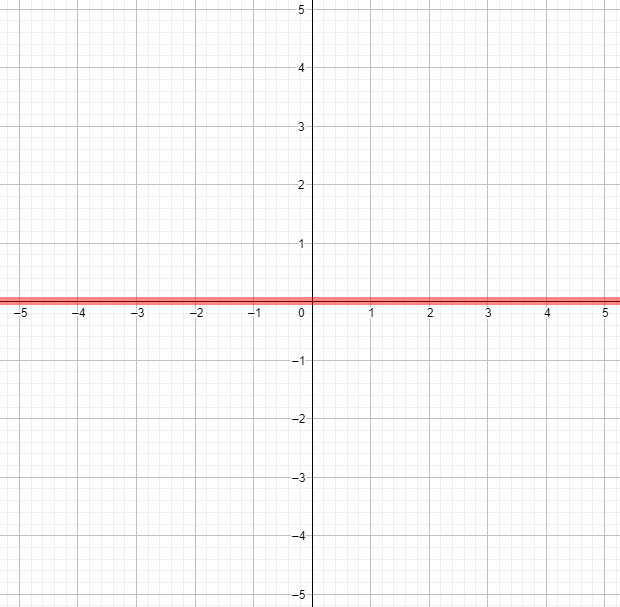ГДЗ по Алгебре 10 Класс Номер 9.30 Профильный Уровень Мордкович — Подробные Ответы

а) у = |[x]|;

б) у = x + [x];

в) у = {x) + [x];

г) у = [{x}].

a) $y = |[x]|$

Если $x > 0$, тогда:

$$y = [x] = k;$$ $$k \leq x < k + 1;$$

Если $x < 0$, тогда:

$$y = -[x] = k;$$ $$[x] = -k;$$ $$-k \leq x < -k + 1;$$

График функции:

Ответ: не является.

б) $y = x + [x]$

Решение равенства:

$$k \leq x < k + 1 \quad \Rightarrow \quad [x] = k;$$ $$2k \leq x + [x] < 2k + 1;$$ $$2k \leq y < 2k + 1;$$

График функции:

Ответ: не является.

в) $y = \{x\} + [x]$

Решение равенства:

$$y = \{x\} + [x] = (x — [x]) + [x] = x;$$ $$y = x;$$

График функции:

Ответ: не является.

г) $y = [[x]]$

Решение равенства:

$$k \leq x < k + 1;$$ $$0 \leq \{x\} < 1;$$ $$[[x]] = 0;$$ $$y = 0;$$

График функции:

Ответ: является.

a) $y = |[x]|$

1) Разбор для $x > 0$:

Для $x > 0$, целая часть $[x] = k$, где $k \in \mathbb{Z}$ — это наибольшее целое число, которое не превышает $x$. Это значит, что:

$$k \leq x < k + 1.$$

Следовательно:

$$y = |[x]| = |k| = k \quad \text{(так как \( k \geq 0 \) при \( x > 0 \))}.$$

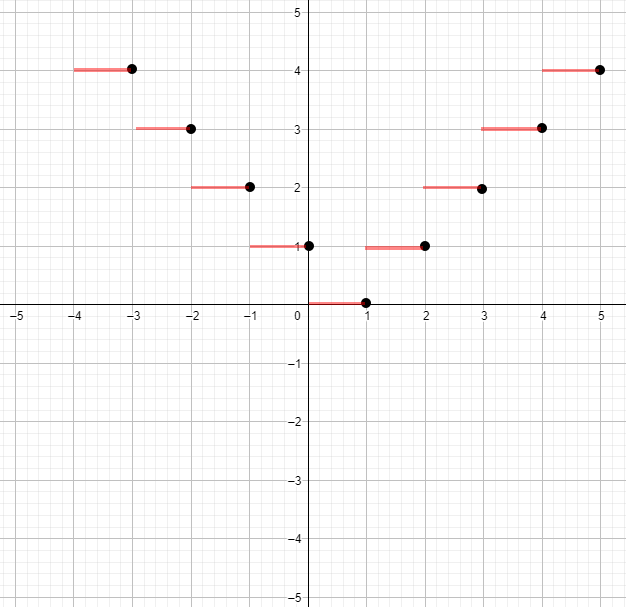
Графически функция $y = |[x]|$ будет выглядеть как ступенчатая функция, где каждый «степ» будет находиться на уровне $k$, где $k$ — целая часть $x$.

2) Разбор для $x < 0$:

Для $x < 0$, целая часть $[x] = -k$, где $k \in \mathbb{Z}$ — это наибольшее целое число, которое не превышает $x$. Это значит, что:

$$-k \leq x < -k + 1.$$

Теперь, так как функция включает абсолютное значение целой части, получаем:

$$y = |[x]| = |-k| = k.$$

Таким образом, для $x < 0$ функция тоже возвращает положительные значения, и $y = k$, где $k$ — положительное целое число, соответствующее целой части отрицательного числа $x$.

3) График функции $y = |[x]|$:

График функции будет ступенчатым. При $x > 0$ он будет следовать за целыми частями $[x]$, но все значения функции будут положительными (так как используется абсолютная величина). Для $x < 0$ график также будет ступенчатым, но с такими же значениями на каждом шаге, только для отрицательных значений $x$ функция будет возвращать положительные значения.

Ответ: График функции $y = |[x]|$ не является функцией с непрерывным или гладким переходом, так как она является разрывной на каждом целочисленном значении $x$.

б) $y = x + [x]$

1) Разбор для любого $x$:

Пусть $[x] = k$, где $k \in \mathbb{Z}$ — целая часть числа $x$. Это означает, что:

$$k \leq x < k + 1.$$

Теперь выразим $y$ как сумму $x$ и $[x]$:

$$y = x + [x] = x + k.$$

Поскольку $k \leq x < k + 1$, это означает, что $y$ будет варьироваться на интервале от $2k$ до $2k + 1$, то есть:

$$2k \leq y < 2k + 1.$$

Таким образом, для каждого целого значения $k$, функция $y$ будет принимать значения в интервале от $2k$ до $2k + 1$.

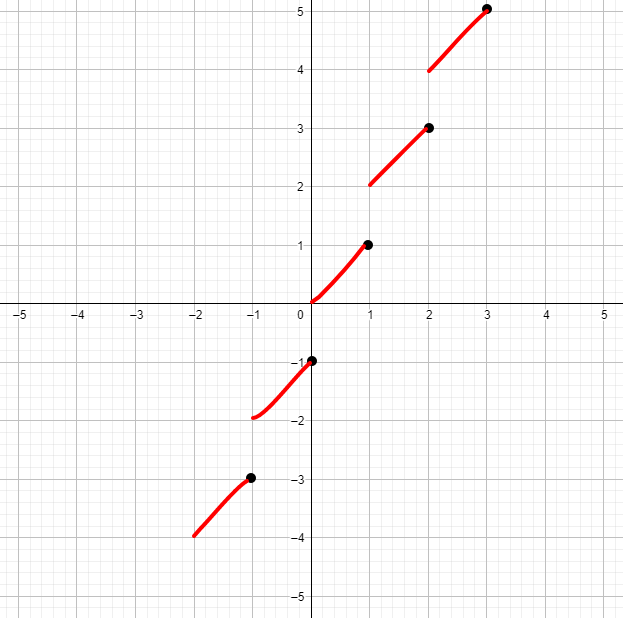
2) График функции $y = x + [x]$:

График функции будет представлять собой серию отрезков, каждый из которых начинается в точке $2k$ и заканчивается в точке $2k + 1$. График будет разрывным, так как каждый отрезок будет соединять значения, соответствующие одному целому числу $k$, и скачок будет происходить на каждом целочисленном значении $x$.

Ответ: График функции $y = x + [x]$ не является гладким и непрерывным, так как это ступенчатая функция с разрывами на каждом целочисленном значении $x$.

в) $y = \{x\} + [x]$

1) Разбор для любого $x$:

Пусть $x = [x] + \{x\}$, где $[x]$ — целая часть числа $x$, а $\{x\} = x — [x]$ — дробная часть числа $x$. Подставим это в выражение для $y$:

$$y = \{x\} + [x] = (x — [x]) + [x] = x.$$

Таким образом, функция $y = \{x\} + [x]$ просто равна $x$, так как дробная и целая части числа $x$ в сумме дают $x$.

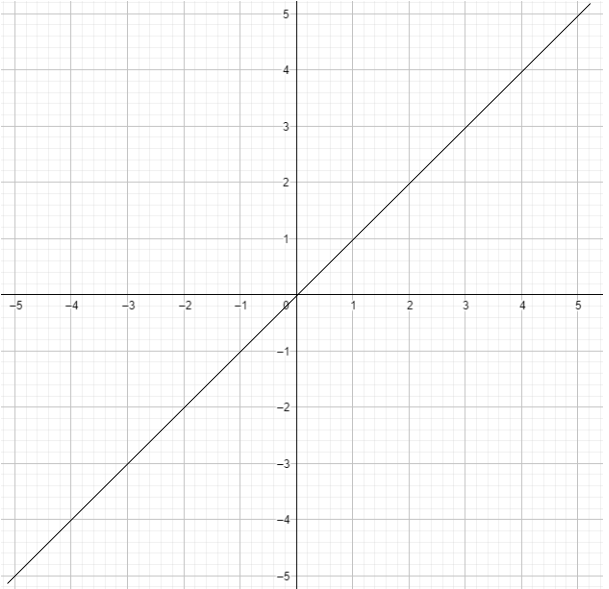
2) График функции $y = \{x\} + [x]$:

Поскольку $y = x$, график этой функции будет прямой линией с угловым коэффициентом 1, проходящей через начало координат. Это линейная функция с непрерывным и гладким графиком.

Ответ: График функции $y = \{x\} + [x]$ является прямой, что означает, что она является линейной и непрерывной функцией.

г) $y = [[x]]$

1) Разбор для $x$:

Пусть $x$ находится в интервале $k \leq x < k + 1$, где $k \in \mathbb{Z}$ — целая часть числа $x$. Тогда дробная часть $\{x\}$ лежит в интервале $0 \leq \{x\} < 1$.

Теперь рассмотрим выражение $[[x]]$. Это означает, что мы берём целую часть дробной части $\{x\}$. Так как $0 \leq \{x\} < 1$, то:

$$[[x]] = 0.$$

Следовательно:

$$y = 0.$$

2) График функции $y = [[x]]$:

График функции $y = [[x]]$ будет горизонтальной прямой, лежащей на уровне $y = 0$ для всех значений $x$, так как для любого $x$ дробная часть $\{x\}$ всегда будет лежать в интервале от 0 до 1, а её целая часть всегда равна 0.

Ответ: График функции $y = [[x]]$ является горизонтальной прямой, лежащей на оси $y = 0$, то есть функция постоянна и равна 0 для всех значений $x$.