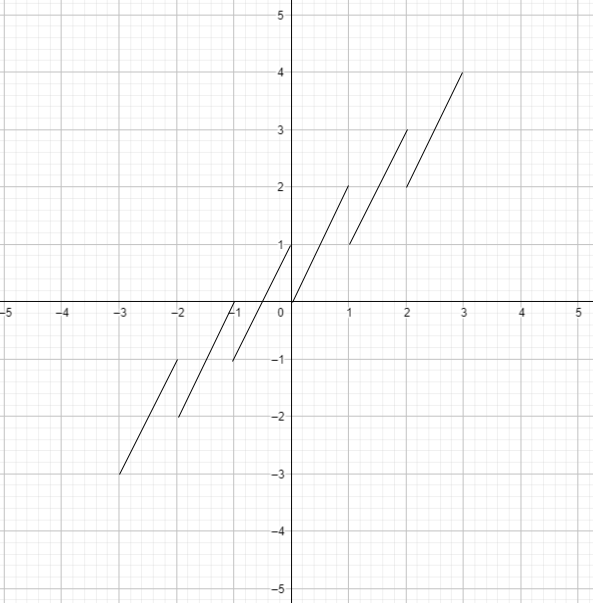ГДЗ по Алгебре 10 Класс Номер 9.32 Профильный Уровень Мордкович — Подробные Ответы

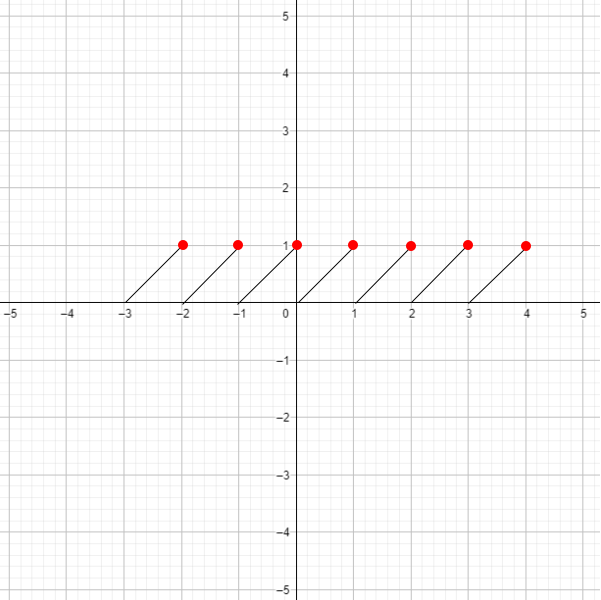
а) у = |{х}|;

б) у = x + {x};

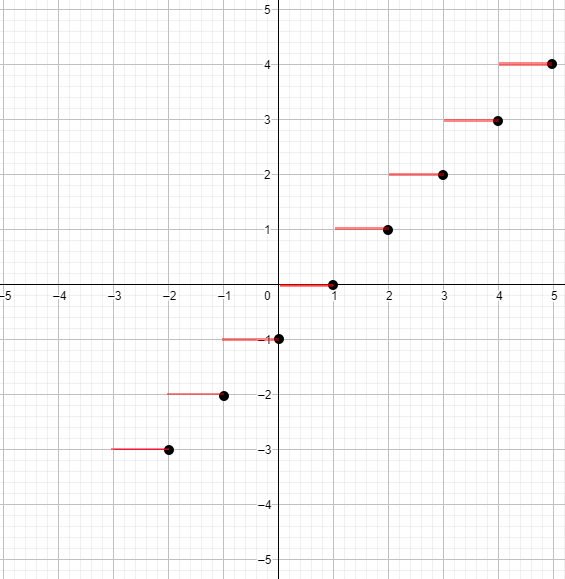
в) у = x — {x};

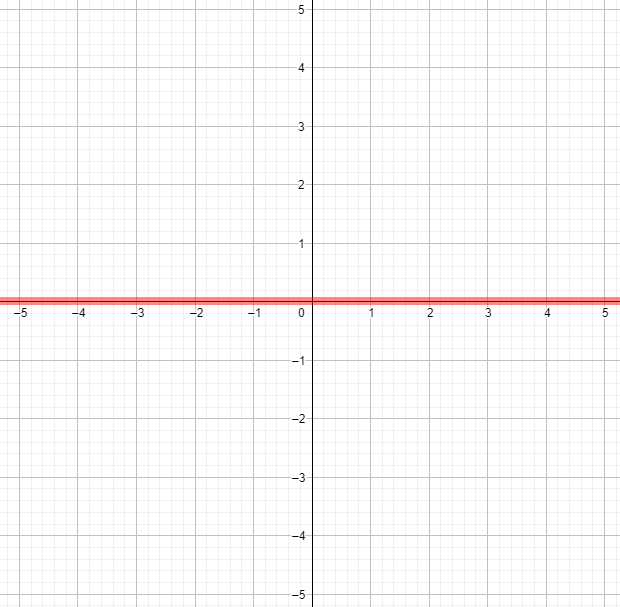
г) у = {[x]}.

а) $y = | \{ x \} | = | x — [x] |$;

Пусть $[x] = k$, тогда:

$$k \leq x < k + 1;$$ $$0 \leq x — [x] < 1;$$ $$0 \leq y < 1;$$

График функции:

Ответ: является.

б) $y = x + \{ x \}$;

Решение равенства:

$$y = x + \{ x \} = x + (x — [x]) = 2x — [x];$$

Решение равенства:

$$k \leq x < k + 1 \quad \Rightarrow \quad [x] = k;$$ $$2k \leq 2x < 2k + 2;$$ $$k \leq 2x — [x] < k + 2;$$ $$k \leq y < k + 2;$$

График функции:

Ответ: не является.

в) $y = x — \{ x \}$;

Решение равенства:

$$y = x — \{ x \} = x — (x — [x]) = [x];$$ $$y = [x] = k;$$ $$k \leq x < k + 1;$$

График функции:

Ответ: не является.

г) $y = \{ [x] \}$;

Решение равенства:

$$k \leq x < k + 1;$$ $$[x] = k;$$ $$[[x]] = [k] = k;$$ $$y = \{ [x] \} = [x] — [[x]] = 0;$$

График функции:

Ответ: является.

а) $y = | \{ x \} | = | x — [x] |$

1) Разбор дробной части $\{ x \}$:

Дробная часть числа $x$ определяется как:

$$\{ x \} = x — [x],$$

где $[x]$ — целая часть числа $x$, то есть наибольшее целое число, не превышающее $x$. Если $x = k + f$, где $k = [x]$ — целая часть числа, а $f = \{x\}$ — дробная, то:

$$x = k + f \quad \text{и} \quad 0 \leq f < 1.$$

Функция $y = | \{ x \} |$ просто берет абсолютное значение дробной части, то есть:

$$y = | \{ x \} | = | x — [x] |.$$

Поскольку $0 \leq \{x\} < 1$, то абсолютное значение $| \{x\} |$ всегда будет равно $\{x\}$, так как дробная часть уже неотрицательна.

2) Доказательство:

• Пусть $[x] = k$, где $k$ — целая часть числа $x$. Это означает:

  $$k \leq x < k + 1.$$

• Тогда дробная часть числа $x$ будет лежать в интервале:

  $$0 \leq x — k < 1.$$

  То есть $\{x\} = x — k$, и, следовательно:

  $$0 \leq y = | \{ x \} | = |x — k| < 1.$$

  Таким образом, функция $y = | \{ x \} |$ всегда лежит в интервале от 0 до 1.

3) График функции:

График функции $y = | \{ x \} |$ будет представлять собой ступенчатую функцию, которая на каждом интервале $k \leq x < k+1$ будет принимать значения от 0 до 1. Так как дробная часть уже неотрицательна, график будет увеличиваться от 0 до 1 и будет симметричен относительно оси $y$ для каждого интервала.

Ответ: Функция является периодической с периодом 1, и её график — ступенчатая функция, которая плавно увеличивается от 0 до 1 и затем возвращается к 0.

б) $y = x + \{ x \}$

1) Разбор выражения $y = x + \{ x \}$:

Используем определение дробной части:

$$\{ x \} = x — [x],$$

где $[x] = k$, целая часть числа $x$. Это означает, что:

$$k \leq x < k + 1 \quad \Rightarrow \quad [x] = k.$$

Теперь подставим дробную часть $\{x\}$ в выражение для $y$:

$$y = x + \{ x \} = x + (x — [x]) = 2x — [x].$$

Итак, мы получили выражение для $y$:

$$y = 2x — [x].$$

2) Дальнейшее разложение:

Пусть $[x] = k$, тогда:

$$k \leq x < k + 1 \quad \Rightarrow \quad 2k \leq 2x < 2k + 2.$$

Преобразуем выражение для $y$:

$$k \leq 2x — [x] < k + 2,$$

и, следовательно:

$$k \leq y < k + 2.$$

Таким образом, функция $y$ будет находиться в интервале от $k$ до $k + 2$, что означает, что каждый «степ» функции будет иметь длину 2 и будет изменяться на интервале от $k$ до $k + 2$.

3) График функции:

График функции $y = x + \{ x \}$ будет ступенчатым, с каждым шагом длиной 2, а на каждом интервале $k \leq x < k + 1$ значение функции будет увеличиваться от $k$ до $k + 2$. Таким образом, функция не является линейной.

Ответ: График функции не является периодическим, так как значения функции изменяются на интервале длиной 2 и не представляют собой обычную ступенчатую структуру с периодом 1.

в) $y = x — \{ x \}$

1) Разбор выражения $y = x — \{ x \}$:

Используем определение дробной части:

$$\{ x \} = x — [x],$$

где $[x] = k$, целая часть числа $x$. Это означает:

$$k \leq x < k + 1 \quad \Rightarrow \quad [x] = k.$$

Теперь подставим дробную часть $\{x\}$ в выражение для $y$:

$$y = x — \{ x \} = x — (x — [x]) = [x] = k.$$

Таким образом, функция $y = x — \{x\}$ просто возвращает целую часть числа $x$, то есть:

$$y = [x].$$

2) График функции:

График функции $y = x — \{ x \}$ будет представлять собой ступенчатую функцию, где значение функции будет равным целой части числа $x$ для каждого интервала $k \leq x < k + 1$. График будет представлять собой последовательность горизонтальных отрезков на каждом интервале $k \leq x < k + 1$, и значения функции будут равны целым числам $k$.

Ответ: Функция не является периодической, так как её график состоит из горизонтальных отрезков, каждый из которых соответствует целой части $x$, и эти отрезки не изменяются с периодом 1.

г) $y = \{ [x] \}$

1) Разбор выражения $y = \{ [x] \}$:

Определим, что такое $[x]$ и $\{[x]\}$:

$$[x] = k, \quad \text{где} \quad k \in \mathbb{Z}.$$

Теперь рассмотрим выражение $y = \{ [x] \}$. Поскольку $[x]$ — целое число, то его дробная часть $\{ [x] \}$ всегда будет равна 0. То есть:

$$\{ [x] \} = [x] — [[x]] = 0.$$

Таким образом, $y = 0$ для всех $x$.

2) График функции:

График функции $y = \{ [x] \}$ будет представлять собой горизонтальную прямую на уровне $y = 0$, так как дробная часть целого числа всегда равна 0.

Ответ: Функция является постоянной, равной 0 для всех значений $x$.