ГДЗ по Алгебре 10 Класс Номер 9.35 Профильный Уровень Мордкович — Подробные Ответы

Постройте график функции:

а) $y = (\{x\})^2$;

в) $y = \sqrt{\{x\}}$;

б) $y = \frac{1}{\{x\}}$;

г) $y = \frac{\{x\} — 1}{1 — 2\{x\}}$.

Выясните, может ли функция быть периодической, если она обладает указанным свойством; если может, то приведите пример, если не может, — объясните почему.

Основной период функции $y = \{x\}$ равен единице, при этом на интервале $[0; 1)$ эта функция задана уравнением $y = x$.

а) $y = (\{x\})^2$;

На интервале $[0; 1)$ имеем функцию:

$$y = x^2;$$ $$x_0 = 0 \quad \text{и} \quad y_0 = 0;$$ $$a = 1 > 0 \quad \text{— ветви направлены вверх;}$$

График функции:

б) $y = \frac{1}{\{x\}}$;

На интервале $[0; 1)$ имеем функцию:

$$y = \frac{1}{x};$$ $$x_0 = 0 \quad \text{и} \quad y_0 = 0;$$ $$k = 1 > 0 \quad \text{— функция убывает;}$$

График функции:

в) $y = \sqrt{\{x\}}$;

На интервале $[0; 1)$ имеем функцию:

$$y = \sqrt{x};$$ $$x_0 = 0 \quad \text{и} \quad y_0 = 0;$$ $$\begin{cases} k = 1 > 0 \\ a = 1 > 0 \end{cases} \quad \text{— функция возрастает;}$$

График функции:

г) $y = \frac{\{x\} — 1}{1 — 2\{x\}}$;

На интервале $[0; 1)$ имеем функцию:

$$y = \frac{x — 1}{1 — 2x} = -\frac{1}{2} \cdot \frac{2 — 2x}{1 — 2x} = -\frac{1}{2} \cdot \frac{1 — 2x + 1}{1 — 2x} = -\frac{1}{2} + \frac{1}{4x — 2};$$ $$x_0 = 0.5 \quad \text{и} \quad y_0 = -0.5;$$ $$k = 1 > 0 \quad \text{— функция убывает;}$$

График функции:

Основной период функции $y = \{x\}$ равен единице, при этом на интервале $[0; 1)$ эта функция задана уравнением $y = x$.

Функция $\{x\}$ называется дробной частью числа $x$. Дробная часть числа $x$ — это то, что остается от числа $x$, если отнять от него целую часть. Например, для $x = 3.25$ дробная часть будет $\{3.25\} = 0.25$.

Основной период функции $y = \{x\}$ равен 1, поскольку дробная часть числа всегда находится в пределах от 0 до 1 (включая 0, но не включая 1). То есть $\{x\}$ повторяется через 1.

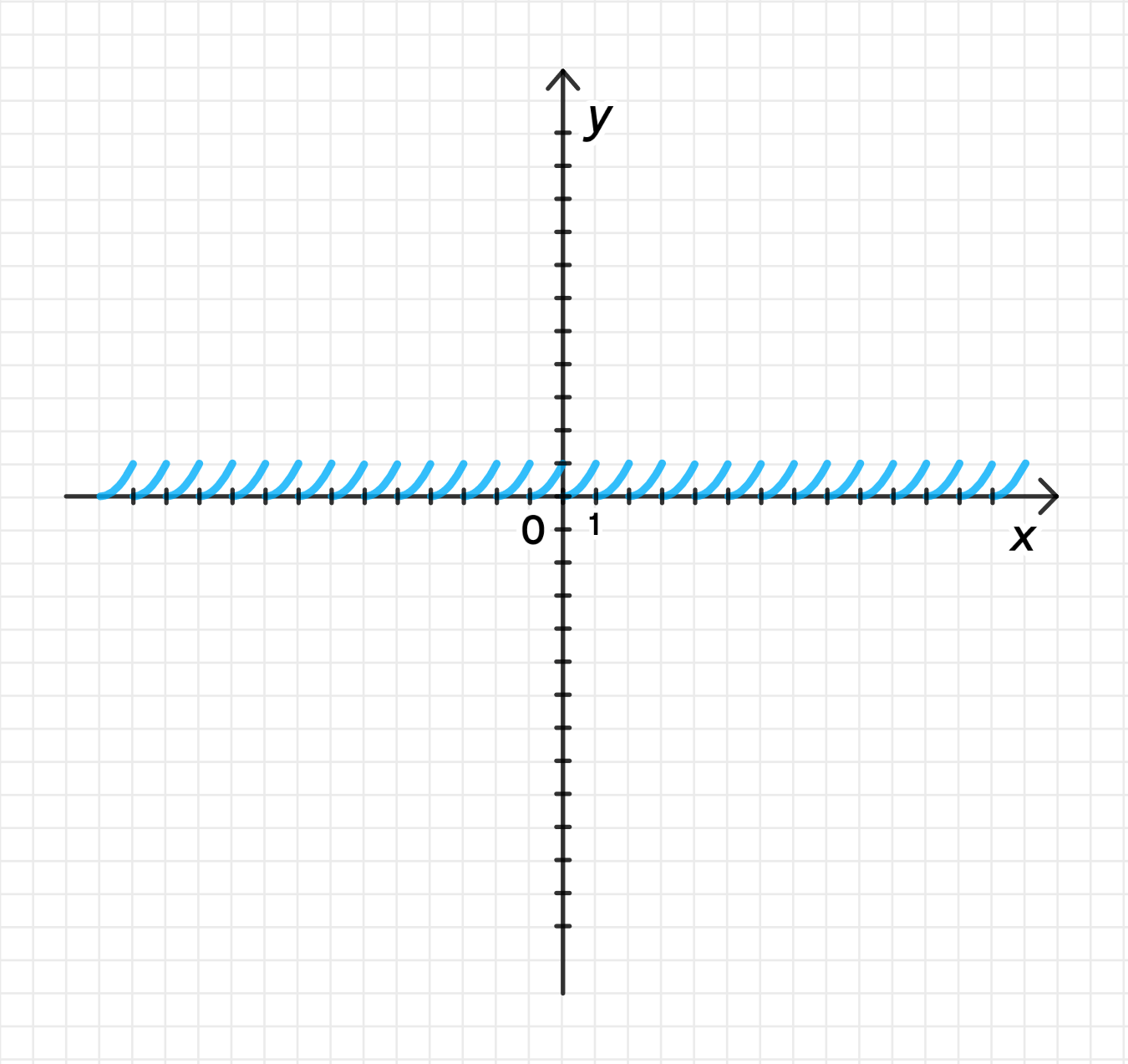
а) $y = (\{x\})^2$;

1) Разбор функции:

• Мы рассматриваем функцию $y = (\{x\})^2$, где $y$ равна квадрату дробной части числа $x$.
• Дробная часть функции на интервале $[0; 1)$ равна самому числу $x$. Таким образом, на интервале $[0; 1)$ функция $y = (\{x\})^2$ примет вид $y = x^2$.

Определим характеристики графика:

• $x_0 = 0$ — точка начала интервала, где значение функции равно $y_0 = 0^2 = 0$.
• $a = 1 > 0$ — функция является квадратичной, и ветви параболы направлены вверх, так как коэффициент при $x^2$ положителен.

Таблица значений функции:

Значения функции для $x = 0$ и $x = 1$ дают $y = 0$ и $y = 1$ соответственно. Обратите внимание, что $x = 1$ в таблице используется как предел интервала, но сама функция на $x = 1$ не определяется.

2) График функции:

График функции $y = x^2$ — это стандартная парабола, направленная вверх. На интервале $[0; 1)$ эта парабола будет начинаться в точке $(0, 0)$ и идти до точки $(1, 1)$.

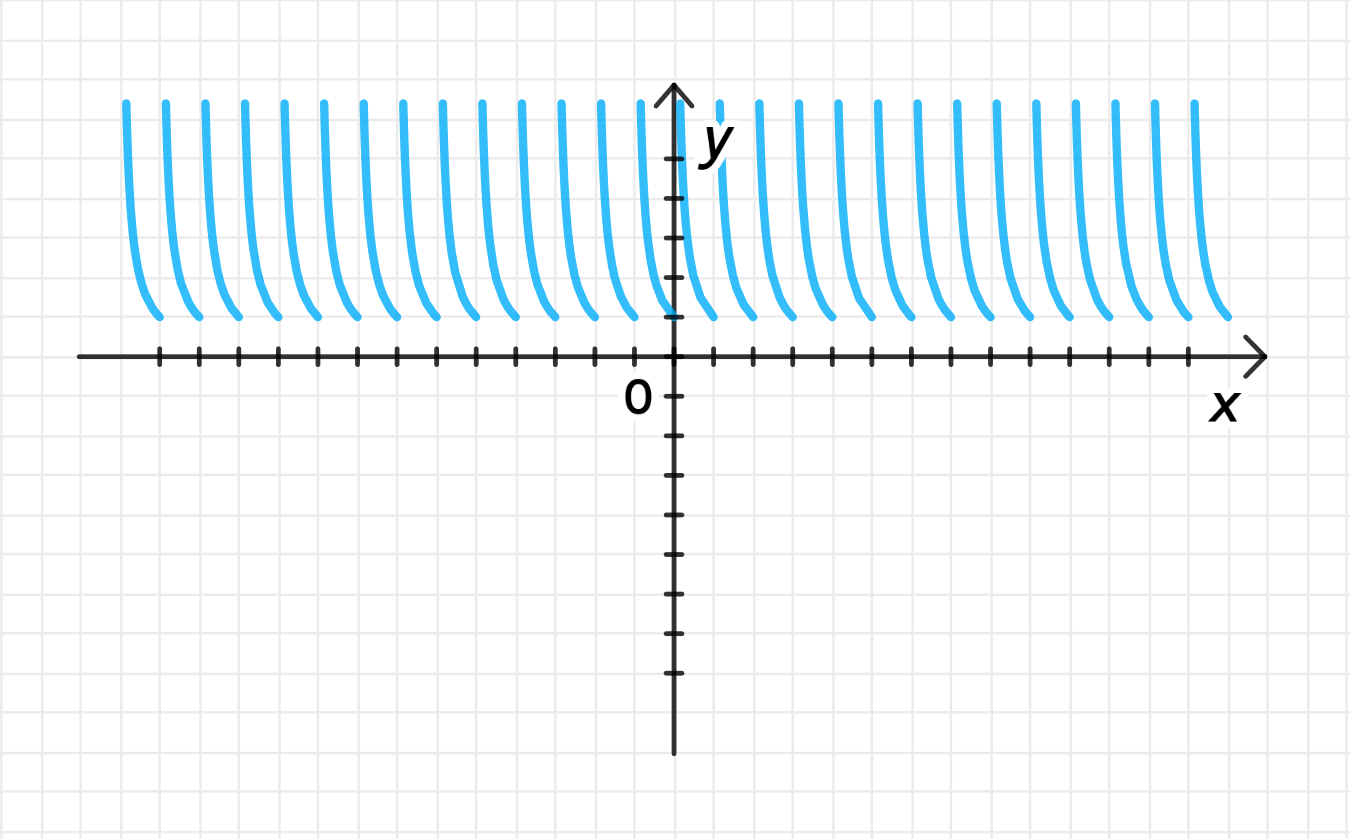
б) $y = \frac{1}{\{x\}}$;

1) Разбор функции:

• Рассматриваем функцию $y = \frac{1}{\{x\}}$, где дробная часть числа $x$ находится на интервале $[0; 1)$, и в этом интервале она не равна нулю.
• На интервале $[0; 1)$, функция будет принимать вид $y = \frac{1}{x}$, поскольку дробная часть равна $x$.

Определим характеристики графика:

• $x_0 = 0$ — точка начала интервала, но функция не определена в точке $x = 0$, поскольку дробная часть $x = 0$ дает деление на ноль.
• $k = 1 > 0$ — функция убывает. Это видно по виду гиперболы, где при $x \to 0^+$, значение функции стремится к бесконечности, а при $x \to 1^-$, значение функции стремится к 1.

Таблица значений функции:

Для $x = 0.5$, мы получаем $y = \frac{1}{0.5} = 2$, а для $x = 1$ значение функции равно $y = \frac{1}{1} = 1$.

2) График функции:

График функции $y = \frac{1}{x}$ на интервале $[0; 1)$ будет гиперболой, которая идет от бесконечности при $x = 0^+$ и стремится к 1, когда $x \to 1^-$.

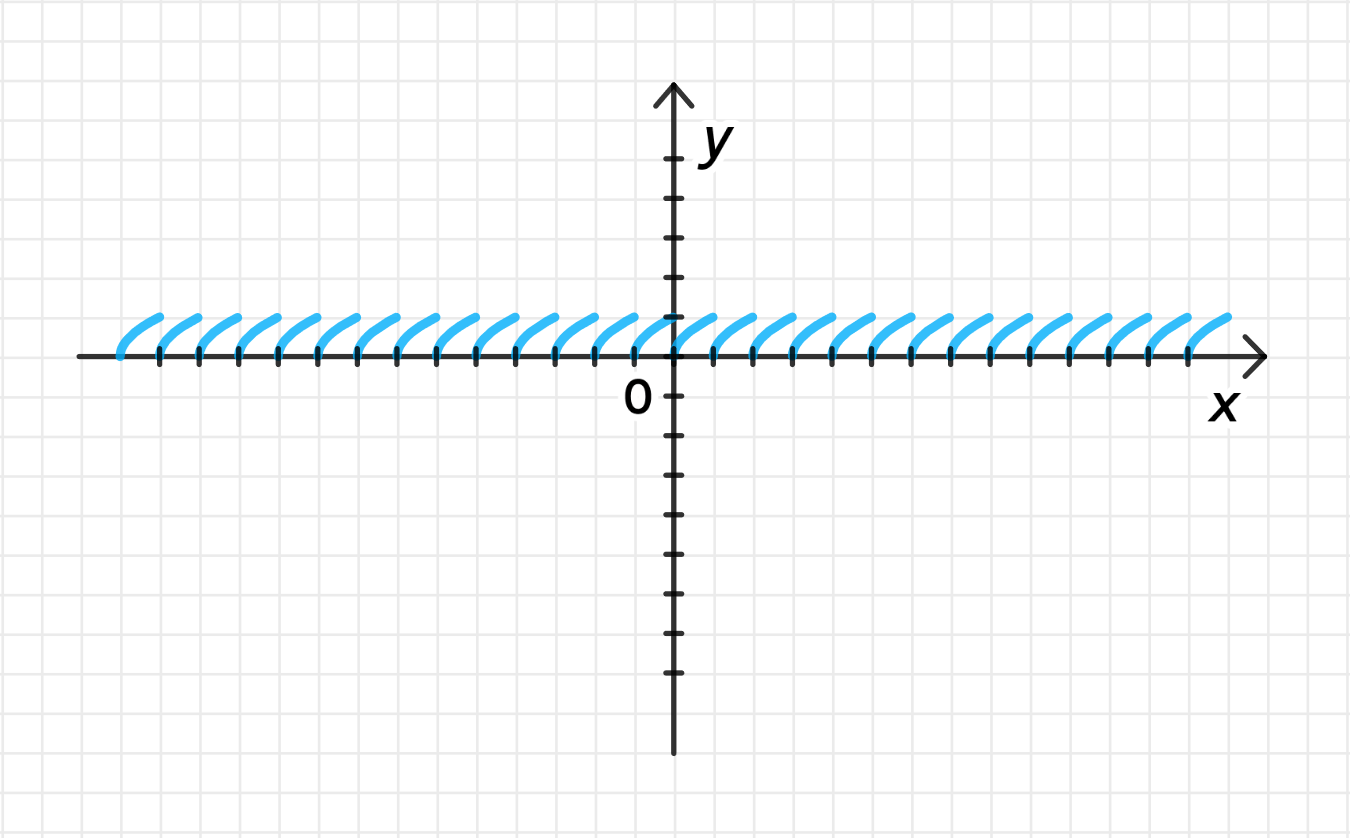
в) $y = \sqrt{\{x\}}$;

1) Разбор функции:

• Рассматриваем функцию $y = \sqrt{\{x\}}$, где дробная часть числа $x$ находится на интервале $[0; 1)$.
• На интервале $[0; 1)$, функция примет вид $y = \sqrt{x}$.

Определим характеристики графика:

• $x_0 = 0$ — точка начала интервала, где значение функции равно $y_0 = \sqrt{0} = 0$.
• $k = 1 > 0$ и $a = 1 > 0$ — функция возрастает. Парабола будет направлена вверх, и значения функции будут увеличиваться с увеличением $x$.

Таблица значений функции:

При $x = 0$, значение функции равно 0, а при $x = 1$, значение функции равно 1.

2) График функции:

График функции $y = \sqrt{x}$ на интервале $[0; 1)$ будет представлять собой кривую, которая начинается в точке $(0, 0)$ и идет до точки $(1, 1)$, при этом график будет возрастать.

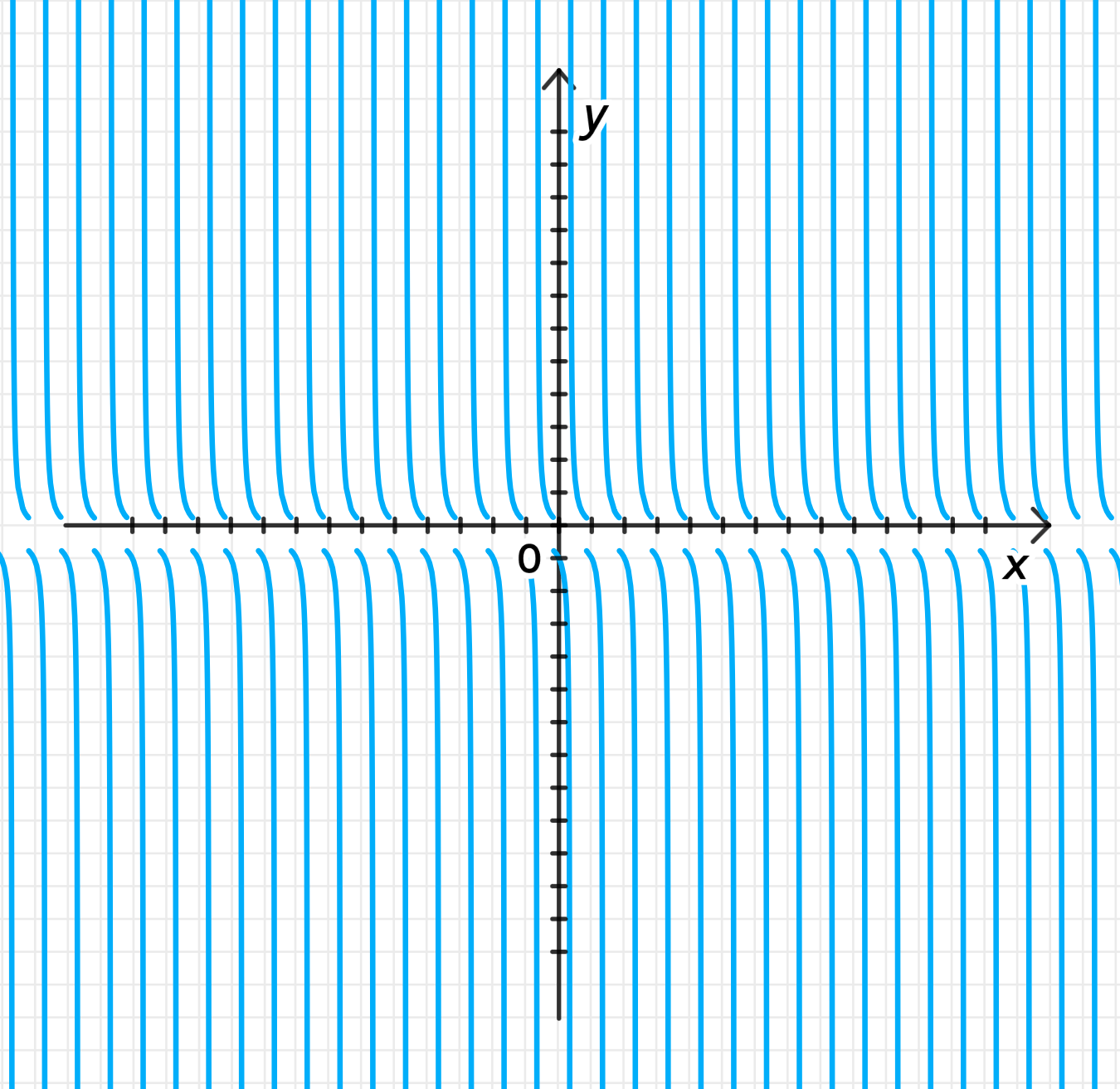
г) $y = \frac{\{x\} — 1}{1 — 2\{x\}}$;

1) Разбор функции:

• Рассматриваем функцию $y = \frac{\{x\} — 1}{1 — 2\{x\}}$.
• На интервале $[0; 1)$, дробная часть $\{x\} = x$, и функция принимает вид:

  $$y = \frac{x — 1}{1 — 2x}$$

Преобразуем выражение:

$$y = -\frac{1}{2} \cdot \frac{2 — 2x}{1 — 2x} = -\frac{1}{2} \cdot \frac{1 — 2x + 1}{1 — 2x} = -\frac{1}{2} + \frac{1}{4x — 2}$$

Определим характеристики графика:

• $x_0 = 0.5$ — критическая точка, в которой знаменатель функции равен нулю.
• $y_0 = -0.5$ — значение функции в этой точке.

Таблица значений функции:

Для $x = 0$, $y = \frac{0 — 1}{1 — 0} = -1$, а для $x = 1$, $y = \frac{1 — 1}{1 — 2} = 0$.

2) График функции:

График функции будет выглядеть как гипербола, у которой на интервале $[0; 1)$ будут резкие изменения, начиная с точки $(0, -1)$ и заканчивая точкой $(1, 0)$.