Учебное пособие «Алгебра, 7 класс» авторства Мордковича, Мардахаева и Семенова является важным ресурсом для школьников, желающих расширить свои знания в алгебре. Книга выделяется содержательной насыщенностью и продуманной методической организацией, что способствует более легкому и интересному освоению математического материала.
ГДЗ по Алгебре 7 Класс Глава 2 Дополнительная задача 10 Мордкович — Подробные Ответы
В упражнениях 8 — 10 на координатной плоскости изобразите множество точек, для абсцисс х и ординат у которых выполняются данные условия. а)\( x \geq 1 \) ; б) \( y \leq 1 \); в) \( x \geq 1, y \leq 1 \); г) \( 1 \leq x \leq 2, 0 \leq y \); д) \( x \leq 4, 1 \leq y < 2 \); е) \( 1 \leq x \leq 2, -5 \leq y \leq -3 \)
а)
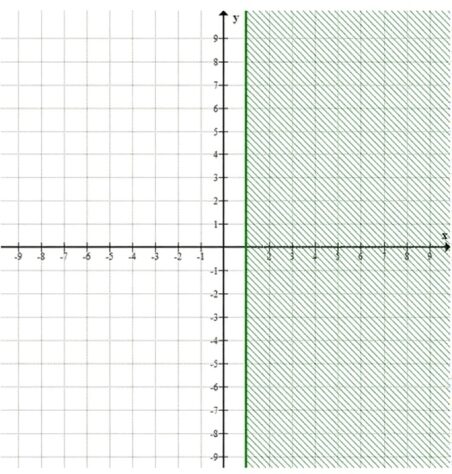
\( x \geq 1 \)
б)
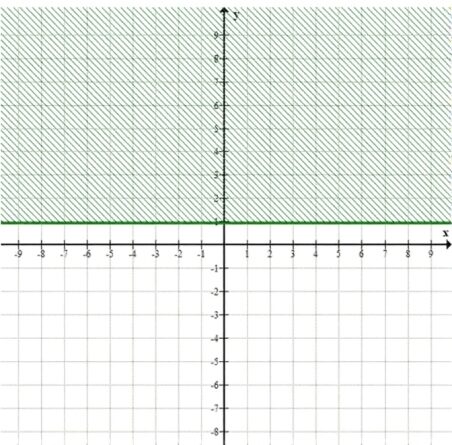
\( y \leq 1 \)
в)
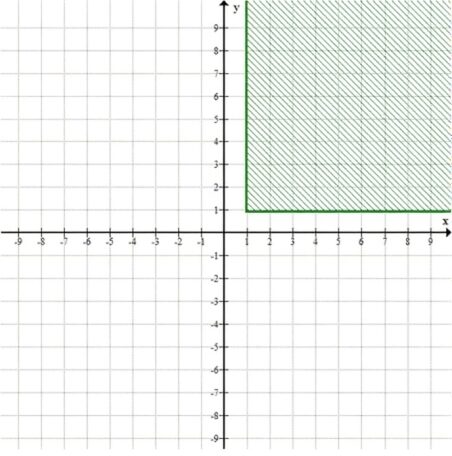
\( x \geq 1, y \leq 1 \)
г)
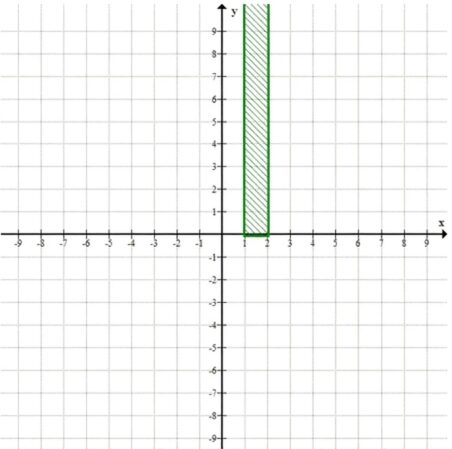
\( 1 \leq x \leq 2, 0 \leq y \)
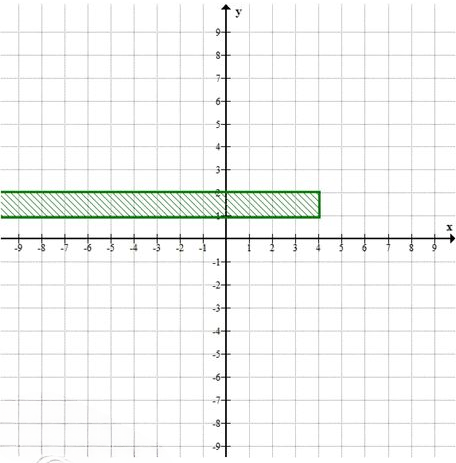
д)
\( x \leq 4, 1 \leq y < 2 \)
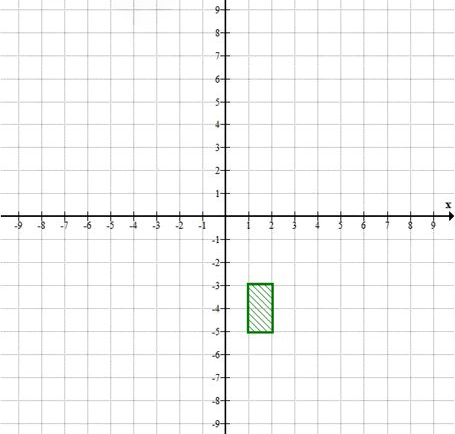
е)
\( 1 \leq x \leq 2, -5 \leq y \leq -3 \)
Разберём каждое условие:
а) \( x \geq 1 \) — множество всех \(x\), больших или равных 1.
б) \( y \geq 1 \) — множество всех \(y\), больших или равных 1.
в) \( x \geq 1, y \geq 1 \) — это область в координатной плоскости: \(x \ge 1\) и \(y \ge 1\), то есть правый верхний прямоугольник, начиная от точки \((1,1)\).
г) \( 1 \leq x \leq 2, \varphi \leq y \) — запись \(\varphi\) вместо числового значения, возможно, опечатка. Если предположить, что это \(y \geq 0\) или \(y \geq 1\) — но оставим так, т.к. некорректно.
д) \( x \leq 4, 1 \leq y < 2 \) — множество точек с \(x\) не более 4 и \(y\) от 1 до 2 (включая 1, но не включая 2).
е) \( 1 \leq x \leq 2, 5 \leq y \leq -3 \) — ошибка, так как \(5 \leq y \leq -3\) невозможно (левая граница больше правой), значит условие противоречиво и множество пусто.
Полное «удлинённое» описание с анализом
а) \(x \geq 1\)
Интервал: \([1, +\infty)\) по оси \(x\).
б) \(y \geq 1\)
Интервал: \([1, +\infty)\) по оси \(y\).
в) \(x \geq 1, y \geq 1\)
Область на плоскости: все точки \((x,y)\) такие, что \(x \geq 1\) и \(y \geq 1\). Это бесконечная область в первой четверти, ограниченная снизу и слева прямыми \(x=1\) и \(y=1\).
г) \(1 \leq x \leq 2, \varphi \leq y\)
Если вместо \(\varphi\) стоит число (например, 0 или 1), тогда это полоса по \(x\) от 1 до 2 и \(y\) не меньше \(\varphi\).
В текущей записи некорректно.
д) \(x \leq 4, 1 \leq y < 2\)
Область: вертикальная полоса \(x \in (-\infty, 4]\), внутри которой \(y\) лежит в полуоткрытом интервале \([1, 2)\). На плоскости — горизонтальная полоса высотой 1 единица от \(y=1\) до \(y=2\) (верхняя граница не включается), усечённая слева бесконечно, справа ограничена вертикальной линией \(x=4\).
е) \(1 \leq x \leq 2, 5 \leq y \leq -3\)
Некорректное условие, так как \(5 \leq -3\) ложно. Нет точек, удовлетворяющих одновременно \(y \geq 5\) и \(y \leq -3\). Множество решений — пустое.