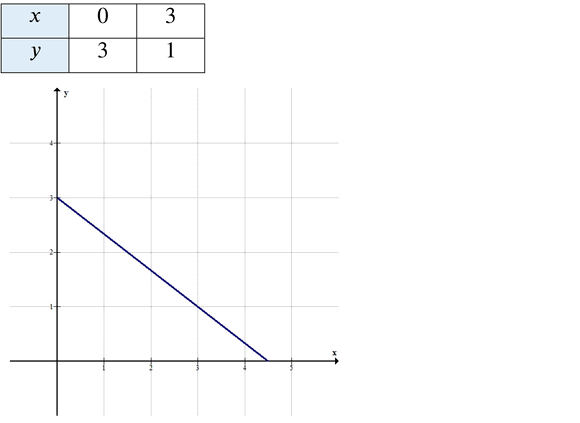ГДЗ по Алгебре 7 Класс Глава 2 Дополнительная задача 17 Мордкович — Подробные Ответы

Аня и Света были в музее Клода Моне во Франции. После посещения музея в кафе Аня заказала 2 чашечки кофе и 3 круассана, а Света заказала 3 чашечки кофе и 2 круассана. Аня заплатила всего 10 евро. Сколько всего заплатила Света, если и Аня, и Света по 1 евро дали официанту, а цена и кофе, и круассана — целые числа в евро?

Пусть чашечка кофе стоит \( x \) евро, а круассан стоит \( y \) евро.
Тогда Аня всего заплатила за кофе и круассаны
\( 2x + 3y \) или \((10 — 1)\) евро.

То есть \( 2x + 3y = 10 — 1 \) или \( 2x + 3y = 9 \).

Света всего заплатила \( 3x + 2y + 1 = m \).

Выразим \( y \) через \( x \) из уравнения \( 2x + 3y = 9 \):
\[ 2x + 3y = 9 \]

\[ 3y = 9 — 2x \]

\[ y = 3 — \frac{2}{3}x. \]

Так как цена и кофе, и круассана – целые числа, то ищем на графике такие \( x \) и \( y \), которые являются целыми числами.
Условие выполняется только при \( x = 3 \) и \( y = 1 \).

Следовательно, кофе стоит 3 евро, а круассан – 1 евро.

Таким образом, Света всего заплатила:
\[ m = 3x + 2y + 1 = 3 \cdot 3 + 2 \cdot 1 + 1 = 9 + 2 + 1 = 12 \, (\text{евро}). \]

Ответ: 12 евро.

Рассмотрим задачу подробно.

Условие:
Аня и Света зашли в буфет. Аня купила 2 чашки кофе и 3 круассана, отдала 10 евро и получила 1 евро сдачи. Света купила 3 чашки кофе и 2 круассана, а также пирожок за 1 евро. Требуется определить, сколько всего евро заплатила Света, если известно, что цены кофе и круассана — целые числа (в евро).

1. Введём переменные.
Пусть:
— \( x \) — цена одной чашки кофе (в евро),
— \( y \) — цена одного круассана (в евро).

2. Составим уравнение для покупки Ани.
Аня купила 2 кофе и 3 круассана, заплатила 10 евро и получила 1 евро сдачи → фактическая стоимость её покупки:

\[
10 — 1 = 9 \text{ евро}.
\]

Уравнение:

\[
2x + 3y = 9.
\]

3. Выразим \( y \) через \( x \).
Из уравнения:

\[
3y = 9 — 2x
\]

\[
y = 3 — \frac{2}{3}x.
\]

4. Учёт целочисленности цен.
Поскольку \( x \) и \( y \) — целые числа (цена в евро без копеек), то \( \frac{2}{3}x \) должно быть целым числом, значит \( x \) кратно 3.

Возможные целые \( x \geq 0 \), \( y \geq 0 \):

— Если \( x = 0 \): \( y = 3 — 0 = 3 \) → кофе бесплатный (маловероятно, но допустим в теории).
— Если \( x = 3 \): \( y = 3 — 2 = 1 \).
— Если \( x = 6 \): \( y = 3 — 4 = -1 \) — не подходит (цена не может быть отрицательной).

Таким образом, возможны два набора цен:

1. \( x = 0,\ y = 3 \),
2. \( x = 3,\ y = 1 \).

5. Выбор реалистичного варианта.
Обычно в задачах такого типа цены положительны для обоих товаров, но вариант \( x = 0 \) формально удовлетворяет условию. Однако если кофе стоит 0 евро, это значит, что Аня заплатила 9 евро только за круассаны, то есть 3 круассана по 3 евро = 9 евро — такое возможно, но тогда Света заплатит:

Для \( x=0, y=3 \):
Покупка Светы: 3 кофе (\(3\cdot 0=0\)), 2 круассана (\(2\cdot 3 = 6\)) и пирожок за 1 евро. Итого:

\[
0 + 6 + 1 = 7 \text{ евро}.
\]

Для \( x=3, y=1 \):
Покупка Светы: 3 кофе (\(3\cdot 3 = 9\)), 2 круассана (\(2\cdot 1 = 2\)), пирожок 1 евро. Итого:

\[
9 + 2 + 1 = 12 \text{ евро}.
\]

6. Проверка условия целых чисел.
Оба варианта дают целые цены. Но, как правило, в таких задачах цены на кофе и круассан ненулевые, и чаще всего ответ — 12 евро, так как это более реалистично для кафе (кофе дороже круассана).

Если предположить, что цена кофе не может быть нулевой, то единственный вариант: \( x=3,\ y=1 \).

7. Итоговый ответ:
Света заплатила:

\[
m = 3x + 2y + 1 = 3\cdot 3 + 2\cdot 1 + 1 = 9 + 2 + 1 = 12 \text{ евро}.
\]

Ответ: 12 евро.