Учебное пособие «Алгебра, 7 класс» авторства Мордковича, Мардахаева и Семенова является важным ресурсом для школьников, желающих расширить свои знания в алгебре. Книга выделяется содержательной насыщенностью и продуманной методической организацией, что способствует более легкому и интересному освоению математического материала.
ГДЗ по Алгебре 7 Класс Глава 2 Дополнительная задача 19 Мордкович — Подробные Ответы
Билет на электричку стоит 70 р., а со скидкой — 50 р. За несколько билетов заплатили 460 р. Сколько всего купили билетов?
Пусть купили \( x \) билетов за 70 р. и \( y \) билетов за 50 р.
За \( x \) билетов заплатили 70\( x \) р., а за \( y \) билетов – 50\( y \) р.
Тогда:
\[ 70x + 50y = 460 \]
\[ 50y = 460 — 70x \]
\[ y = \frac{460}{50} — \frac{70}{50}x \]
\[ y = -1,4x + 9,2 \]
Количество билетов может быть только целым числом.
Значит, купили \( x = 3 \) билета за 70 р. и \( y = 5 \) билетов за 50 р.
Всего купили:
\[ 3 + 5 = 8 \, (\text{билетов}). \]Ответ: 8 билетов.
Условие:
На 460 рублей купили несколько билетов по 70 рублей и по 50 рублей. Требуется найти общее количество купленных билетов.
Шаг 1. Введение переменных
Пусть:
— \( x \) — количество билетов по 70 рублей;
— \( y \) — количество билетов по 50 рублей.
Тогда общая стоимость покупки:
\[
70x + 50y = 460
\]
Шаг 2. Выражение \( y \) через \( x \)
Решаем уравнение относительно \( y \):
\[
50y = 460 — 70x
\]
\[
y = \frac{460 — 70x}{50}
\]
\[
y = \frac{460}{50} — \frac{70x}{50}
\]
\[
y = 9{,}2 — 1{,}4x
\]
Шаг 3. Целочисленность решения
Поскольку \( x \) и \( y \) — целые неотрицательные числа (количество билетов), найдём допустимые значения.
Из уравнения \( y = 9{,}2 — 1{,}4x \):
1. \( y \geq 0 \Rightarrow 9{,}2 — 1{,}4x \geq 0 \Rightarrow 1{,}4x \leq 9{,}2 \Rightarrow x \leq \frac{9{,}2}{1{,}4} \approx 6{,}57 \), значит \( x \leq 6 \).
2. \( x \) — целое число, \( x \geq 0 \).
3. Подставим целые \( x \) от 0 до 6 и проверим, будет ли \( y \) целым:
— \( x = 0 \): \( y = 9{,}2 \) — не целое.
— \( x = 1 \): \( y = 9{,}2 — 1{,}4 = 7{,}8 \) — не целое.
— \( x = 2 \): \( y = 9{,}2 — 2{,}8 = 6{,}4 \) — не целое.
— \( x = 3 \): \( y = 9{,}2 — 4{,}2 = 5 \) — целое.
— \( x = 4 \): \( y = 9{,}2 — 5{,}6 = 3{,}6 \) — не целое.
— \( x = 5 \): \( y = 9{,}2 — 7 = 2{,}2 \) — не целое.
— \( x = 6 \): \( y = 9{,}2 — 8{,}4 = 0{,}8 \) — не целое.
Единственное целое решение: \( x = 3 \), \( y = 5 \).
Шаг 4. Проверка
\[
70 \cdot 3 + 50 \cdot 5 = 210 + 250 = 460
\]
Сумма сходится.
Шаг 5. Общее количество билетов
\[
x + y = 3 + 5 = 8
\]
Ответ: 8 билетов.
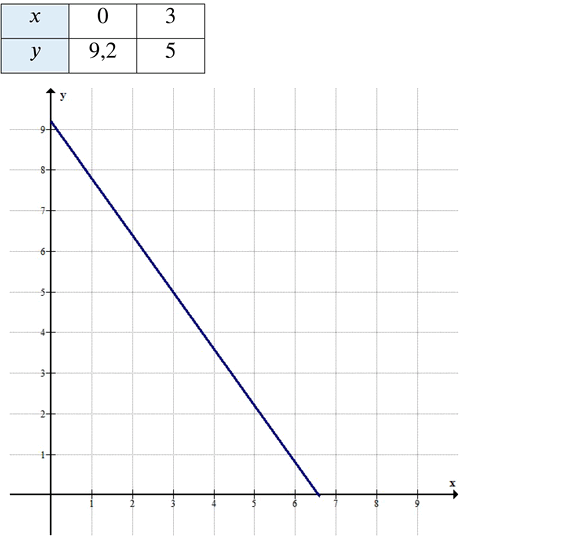
Примечание: в таблице в исходном решении указаны значения \( y \) при \( x = 0 \) и \( x = 3 \), чтобы показать, что только при \( x = 3 \) получается целое \( y \).