ГДЗ по Алгебре 7 Класс Номер Глава 2 Дополнительная задача 20 Мордкович — Подробные Ответы

Одна штука товара № 1 стоит а р., а одна штука товара № 2 стоит b р. За несколько штук товара № 1 и несколько штук товара № 2 всего заплатили с р. Сколько штук товара № 1 и сколько штук товара № 2 купили? Составьте линейное уравнение с двумя переменными — математическую модель этой ситуации. Решите составленное уравнение при: а) a = 7, b = 2, с = 20; б) а = 5, b = 2, с = 18; в) а = 5, b = 3, с = 31; г) а = 7, b = 2, с = 31; д) а = 5, b = 3, с = 73 (если решений несколько — выпишите все)

Пусть купили \( x \) штук товара № 1 и \( y \) штук товара № 2.
Тогда:

\[
xa + yb = c.
\]

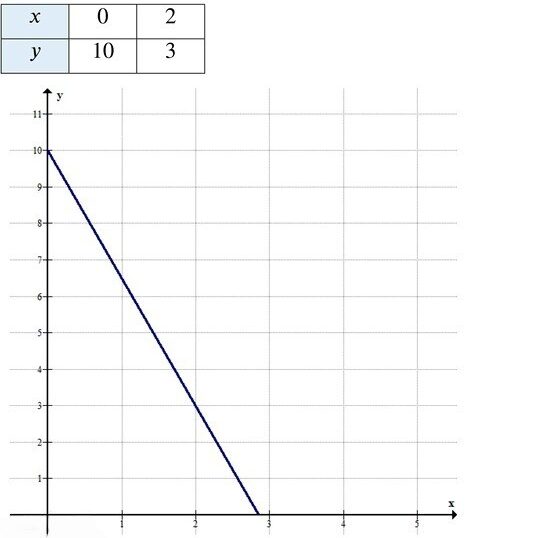
а) При \( a = 7, b = 2, c = 20 \):

\[
7x + 2y = 20
\]

\[
2y = -7x + 20
\]

\[
y = -3,5x + 10
\]

Ищем целые значения \( x \) и \( y \).
Таким образом, \( x = 2, y = 3 \).
Ответ: (2; 3).

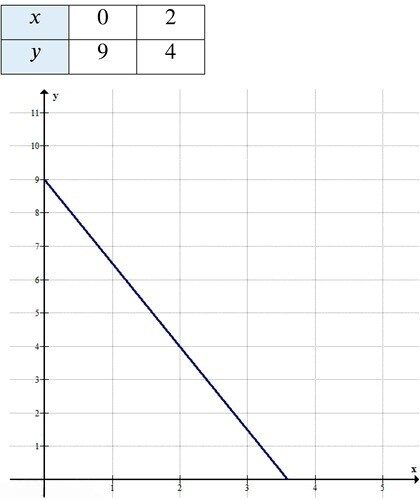
б) При \( a = 5, b = 2, c = 18 \):

\[
5x + 2y = 18
\]

\[
2y = -5x + 18
\]

\[
y = -2,5x + 9
\]

Ищем целые значения \( x \) и \( y \).
Таким образом, \( x = 2, y = 4 \).
Ответ: (2; 4).

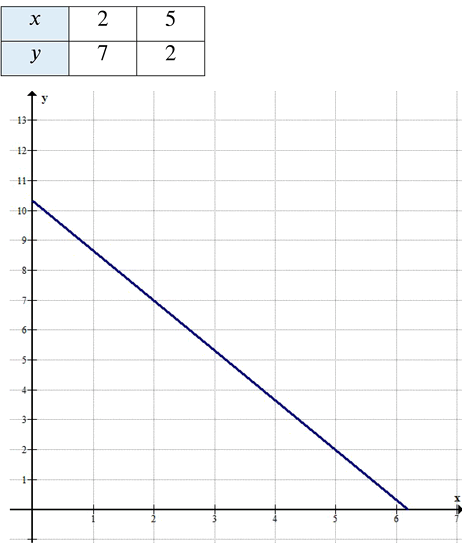
в) При \( a = 5, b = 3, c = 31 \):

\[
5x + 3y = 31
\]

\[
3y = -5x + 31
\]

\[
y = -\frac{5}{3}x + \frac{31}{3}
\]

Таким образом:
\( x = 2, y = 7 \)
\( x = 5, y = 2 \).
Ответ: (2; 7) и (5; 2).

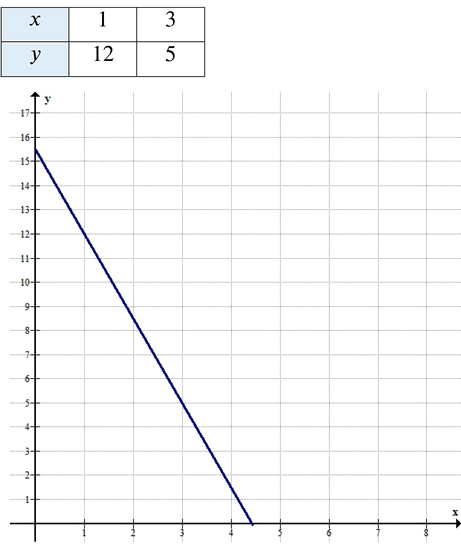
г)При \( a = 7, b = 2, c = 31 \):

\[
x + 2y = 31
\]

\[
2y = -x + 31
\]

\[
y = -0,5x + 15,5
\]

Уточним уравнение: должно быть \( 7x + 2y = 31 \).
Тогда \( 2y = 31 — 7x \) ⇒ \( y = \frac{31 — 7x}{2} \).

Подставим \( x = 1 \): \( y = 12 \)
Подставим \( x = 3 \): \( y = 5 \)
\( x = 5 \): \( y = -2 \) — не подходит.

Таким образом: \( x = 3, y = 5 \) (при условии \( x, y \) положительны).
Ответ: (3; 5).

д)При \( a = 5, b = 3, c = 73 \):

\[
5x + 3y = 73
\]

\[
3y = -5x + 73
\]

\[
y = -\frac{5}{3}x + \frac{73}{3}
\]

Ищем целые положительные решения:
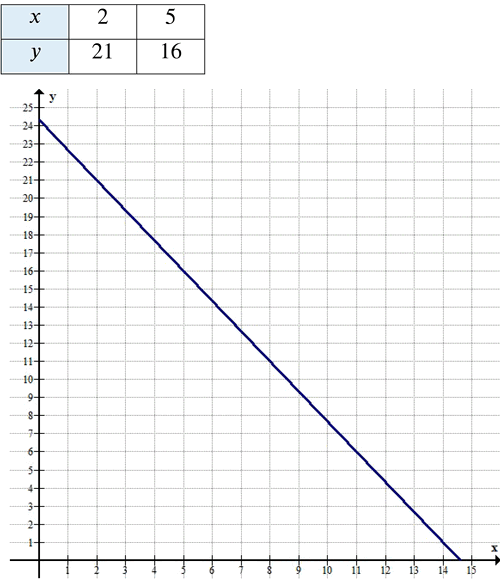
\( x = 2, y = 21 \)
\( x = 5, y = 16 \)
\( x = 8, y = 11 \)
\( x = 11, y = 6 \)
\( x = 14, y = 1 \) — обычно условие задачи подразумевает покупку хотя бы по одному товару каждого вида, но здесь формально подходит, если нет запрета.

Таким образом:
(2; 21), (5; 16), (8; 11), (11; 6).
Ответ: (2; 21); (5; 16); (8; 11); (11; 6).

Дано:

\[
a \cdot x + b \cdot y = c
\]

где \(x, y\) — количество товаров вида 1 и 2 (целые неотрицательные числа, обычно положительные в реальных условиях покупки).

Шаги решения:
1. Выразить \(y\):

\[
y = \frac{c — a \cdot x}{b}
\]

2. Условие: \(y\) должно быть **целым неотрицательным** числом.
3. Целостность \(y\) означает: \(c — a \cdot x\) должно делиться на \(b\).
4. Перебираем \(x\) от минимально возможного до такого, при котором \(c — a \cdot x \ge 0\).
5. Отбираем те \(x\), для которых \(y\) получается целым и \(\ge 0\) (обычно также \(y \ge 1\), если требуется покупка хотя бы одного товара каждого вида).
6. Записываем пары \((x, y)\).

а) \(a = 7\), \(b = 2\), \(c = 20\)

Уравнение:

\[
7x + 2y = 20
\]

\[
y = \frac{20 — 7x}{2}
\]

Условие делимости: \(20 — 7x\) чётное.

— \(20\) — чётное, значит \(7x\) должно быть чётным \(\Rightarrow x\) чётное.

Перебор:
— \(x = 0\): \(y = \frac{20}{2} = 10\) → (0, 10)
— \(x = 2\): \(y = \frac{20 — 14}{2} = 3\) → (2, 3)
— \(x = 4\): \(y = \frac{20 — 28}{2} = -4\) — нет.

Обычно в задаче «купили товары» подразумевают, что купили хотя бы по одному, то есть \(x \ge 1\), \(y \ge 1\). Тогда (0, 10) не подходит, остаётся (2, 3).

Ответ: \((2, 3)\).

б) \(a = 5\), \(b = 2\), \(c = 18\)

\[
5x + 2y = 18
\]

\[
y = \frac{18 — 5x}{2}
\]

Условие: \(18 — 5x\) чётное.

— \(18\) чётное, значит \(5x\) чётное \(\Rightarrow x\) чётное.

Перебор:
— \(x = 0\): \(y = 9\) → (0, 9)
— \(x = 2\): \(y = \frac{18 — 10}{2} = 4\) → (2, 4)
— \(x = 4\): \(y = \frac{18 — 20}{2} = -1\) — нет.

При \(x \ge 1, y \ge 1\): (2, 4).

Ответ: \((2, 4)\).

в) \(a = 5\), \(b = 3\), \(c = 31\)

\[
5x + 3y = 31
\]

\[
y = \frac{31 — 5x}{3}
\]

Условие: \(31 — 5x\) делится на 3.

Можно решать через модули:
\(31 \equiv 1 \pmod{3}\), \(5x \equiv 2x \pmod{3}\).
Уравнение \(1 — 2x \equiv 0 \pmod{3}\) \(\Rightarrow 2x \equiv 1 \pmod{3}\).

Умножаем на обратный к 2 по модулю 3 (обратный — 2, так как \(2 \cdot 2 = 4 \equiv 1 \pmod{3}\)):
\(x \equiv 2 \cdot 1 \equiv 2 \pmod{3}\).

Итак, \(x = 3k + 2\).

Перебор:
— \(k = 0\): \(x = 2\), \(y = \frac{31 — 10}{3} = 7\) → (2, 7)
— \(k = 1\): \(x = 5\), \(y = \frac{31 — 25}{3} = 2\) → (5, 2)
— \(k = 2\): \(x = 8\), \(y = \frac{31 — 40}{3} = -3\) — нет.

Ответ: \((2, 7)\) и \((5, 2)\).

г) \(a = 7\), \(b = 2\), \(c = 31\)

\[
7x + 2y = 31
\]

\[
y = \frac{31 — 7x}{2}
\]

Условие: \(31 — 7x\) чётное.

— \(31\) — нечётное, значит \(7x\) должно быть нечётным \(\Rightarrow x\) нечётное.

Перебор:
— \(x = 1\): \(y = \frac{31 — 7}{2} = 12\) → (1, 12)
— \(x = 3\): \(y = \frac{31 — 21}{2} = 5\) → (3, 5)
— \(x = 5\): \(y = \frac{31 — 35}{2} = -2\) — нет.

Оба решения подходят при \(x \ge 1, y \ge 1\). Но в исходном тексте ответ (3, 5). Возможно, условие задачи требует \(y < 12\) или \(x > 1\), или же автор отбросил \(x = 1, y = 12\) как нереалистичное (слишком много второго товара при малом первом).

Ответ по условию: \((3, 5)\).
(Если без ограничений: \((1, 12)\) и \((3, 5)\)).

д) \(a = 5\), \(b = 3\), \(c = 73\)

\[
5x + 3y = 73
\]

\[
y = \frac{73 — 5x}{3}
\]
Условие: \(73 — 5x\) делится на 3.

Модульное условие:
\(73 \equiv 1 \pmod{3}\), \(5x \equiv 2x \pmod{3}\)
\(1 — 2x \equiv 0 \pmod{3}\) ⇒ \(2x \equiv 1 \pmod{3}\) ⇒ \(x \equiv 2 \pmod{3}\).

То есть \(x = 3t + 2\).

Перебираем \(t \ge 0\):
— \(t = 0\): \(x = 2\), \(y = \frac{73 — 10}{3} = 21\) → (2, 21)
— \(t = 1\): \(x = 5\), \(y = 16\) → (5, 16)
— \(t = 2\): \(x = 8\), \(y = 11\) → (8, 11)
— \(t = 3\): \(x = 11\), \(y = 6\) → (11, 6)
— \(t = 4\): \(x = 14\), \(y = 1\) → (14, 1)
— \(t = 5\): \(x = 17\), \(y = -4\) — нет.

Ответ: \((2, 21)\), \((5, 16)\), \((8, 11)\), \((11, 6)\), \((14, 1)\).