ГДЗ по Алгебре 7 Класс Глава 2 Дополнительная задача 8 Мордкович — Подробные Ответы

В упражнениях 8 — 10 на координатной плоскости изобразите множество точек, для абсцисс х и ординат у которых выполняются данные условия.

a)\( x = 0, y \ge 0 \)

б)\( x < 0, y = 0 \)

в) \( xy = 0 \)

г)\( \frac{y}{x} = 0 \)

д)\( \frac{x}{y} = 0 \)

е)\( \frac{xy}{x+y} = 0 \)

a)
\( x = 0, y \ge 0 \)

б)
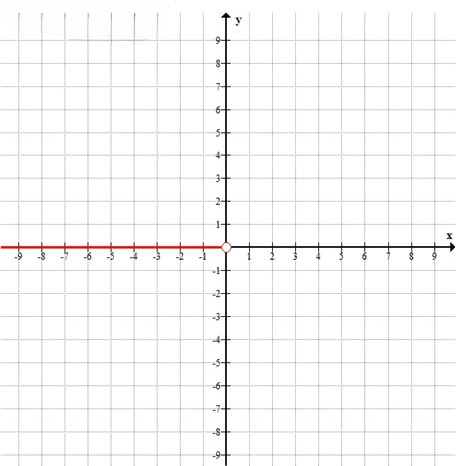
\( x < 0, y = 0 \)

в)
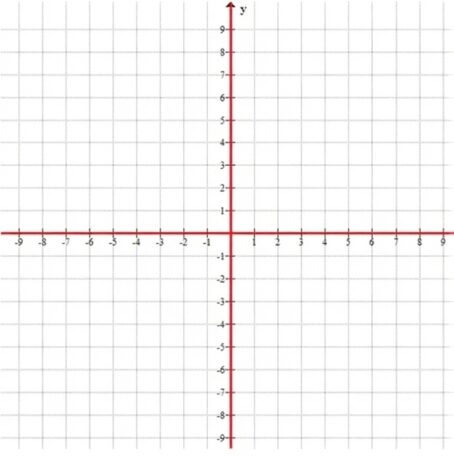
\( xy = 0 \)

г)
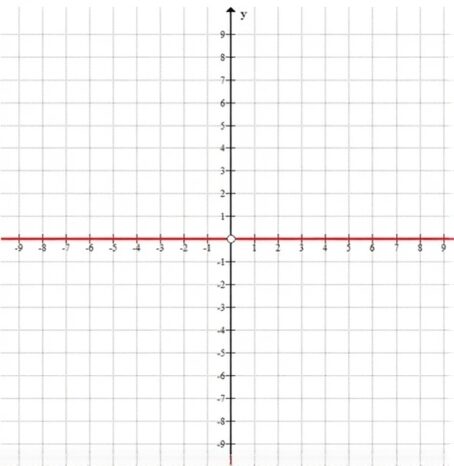
\( \frac{y}{x} = 0 \)

\( y = 0, x \ne 0 \)

д)
\( \frac{x}{y} = 0 \)

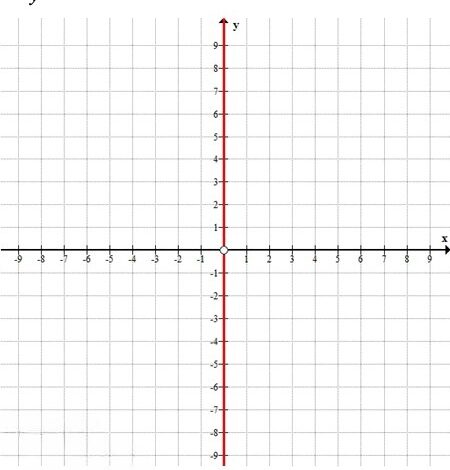
\( x = 0, y \ne 0 \)

е)
\( \frac{xy}{x+y} = 0 \)

\( xy = 0, x+y \ne 0 \)

\( x = 0, y \ne 0 \) или \( y = 0, x \ne 0 \)

В этом задании требуется описать геометрическое место точек на координатной плоскости, удовлетворяющих заданным алгебраическим условиям. Все точки имеют координаты \( (x; y) \), где \( x \) и \( y \) — действительные числа.

а) \( x = 0 \), \( y \geq 0 \)

Условие \( x = 0 \) означает, что точка лежит на оси ординат (\( Oy \)).
Дополнительное условие \( y \geq 0 \) ограничивает её неотрицательной частью оси \( Oy \), то есть включая начало координат и все точки выше него.

Геометрически это — луч, исходящий из начала координат и направленный вверх по оси \( Oy \).

б) \( x < 0 \), \( y = 0 \)

Условие \( y = 0 \) означает, что точка лежит на оси абсцисс (\( Ox \)).
Условие \( x < 0 \) выбирает только те точки, которые находятся левее начала координат.

Геометрически это — открытый луч на оси \( Ox \), направленный влево, не включая точку \( (0; 0) \).

в) \( xy = 0 \)

Произведение \( xy = 0 \) тогда и только тогда, когда хотя бы один из множителей равен нулю:

— либо \( x = 0 \) (вся ось \( Oy \)),
— либо \( y = 0 \) (вся ось \( Ox \)).

Следовательно, множество решений — это объединение двух координатных осей: \( Ox \cup Oy \).
Это крест, образованный осями координат.

г) \( \frac{y}{x} = 0 \)

Дробь равна нулю тогда и только тогда, когда числитель равен нулю, а знаменатель не равен нулю.

— Числитель: \( y = 0 \)
— Знаменатель: \( x \neq 0 \)

Значит, точки лежат на оси \( Ox \), кроме начала координат.

Геометрически — это прямая \( y = 0 \) без точки \( (0; 0) \) — две полуоси \( Ox \) слева и справа от начала.

д) \( \frac{x}{y} = 0 \)

Аналогично: дробь равна нулю, если числитель ноль, а знаменатель не ноль.

— \( x = 0 \)
— \( y \neq 0 \)

Точки лежат на оси \( Oy \), кроме начала координат.

Геометрически — это прямая \( x = 0 \) без точки \( (0; 0) \) — верхняя и нижняя полуоси оси \( Oy \).

е) \( \frac{xy}{x + y} = 0 \)

Дробь равна нулю, если числитель равен нулю, а знаменатель не равен нулю.

Числитель: \( xy = 0 \) ⇒ \( x = 0 \) или \( y = 0 \)
Знаменатель: \( x + y \neq 0 \) ⇒ \( y \neq -x \)

Рассмотрим два случая:

1. Если \( x = 0 \): тогда условие \( x + y \neq 0 \) превращается в \( y \neq 0 \).
→ Получаем ось \( Oy \) без точки \( (0; 0) \).

2. Если \( y = 0 \): тогда \( x + 0 \neq 0 \) ⇒ \( x \neq 0 \).
→ Получаем ось \( Ox \) без точки \( (0; 0) \).

Таким образом, множество решений — это обе координатные оси без начала координат, то есть \( (Ox \cup Oy) \setminus \{(0; 0)\} \).