Учебное пособие «Алгебра, 7 класс» авторства Мордковича, Мардахаева и Семенова является важным ресурсом для школьников, желающих расширить свои знания в алгебре. Книга выделяется содержательной насыщенностью и продуманной методической организацией, что способствует более легкому и интересному освоению математического материала.
ГДЗ по Алгебре 7 Класс Глава 2 Дополнительная задача 9 Мордкович — Подробные Ответы
В упражнениях 8 — 10 на координатной плоскости изобразите множество точек, для абсцисс х и ординат у которых выполняются данные условия. а) х = 5, |у| = 5; б) |х| = 3, |у| = 1; в)\( 1 \leq x < 2, y = 0 \) ;г)\( 1 < x \leq 2, y = -1 \) д) |х| = 1, 2 < у < 5; е) \( x(x — 1) = 0, y \geq -3 \)
a) x = 5, |y| = 5;
б) |x| = 3, |y| = 1;
в) 1 ≤ x < 2, y = 0;
г) 1 ≤ x ≤ 2, y = -1;
д) |x| = 1, 2 < y < 5;
е) x(x-1) = 0, y ≥ -3;
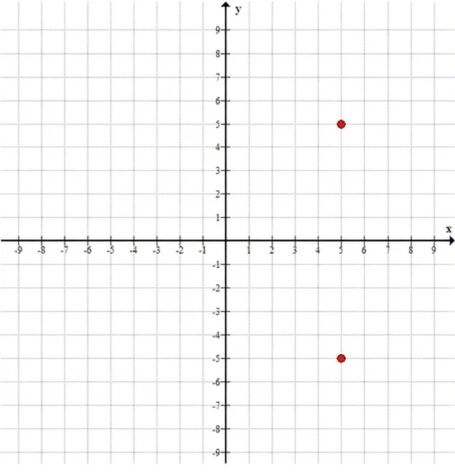
а) \( x = 5, \; |y| = 5 \)
1. \(x = 5\) — вертикальная прямая.
2. \(|y| = 5\) значит \(y = 5\) или \(y = -5\).
3. Значит точки: \((5, 5)\) и \((5, -5)\).
Только две отдельные точки.
График: вертикальная линия \(x=5\), на ней две точки, остальная часть линии не входит.
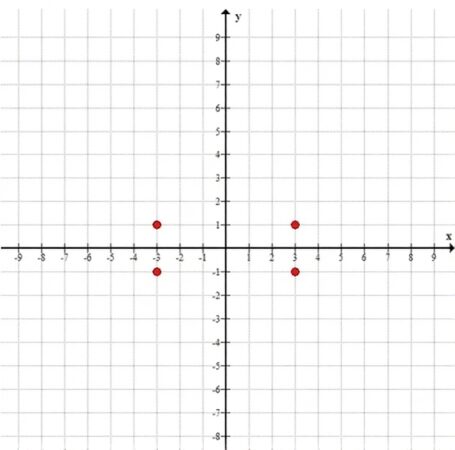
б) \( |x| = 3, \; |y| = 1 \)
1. \(|x| = 3\) ⇒ \(x = 3\) или \(x = -3\).
2. \(|y| = 1\) ⇒ \(y = 1\) или \(y = -1\).
3. Все комбинации: \((3, 1), (3, -1), (-3, 1), (-3, -1)\).
График: четыре отдельные точки (вершины прямоугольника).
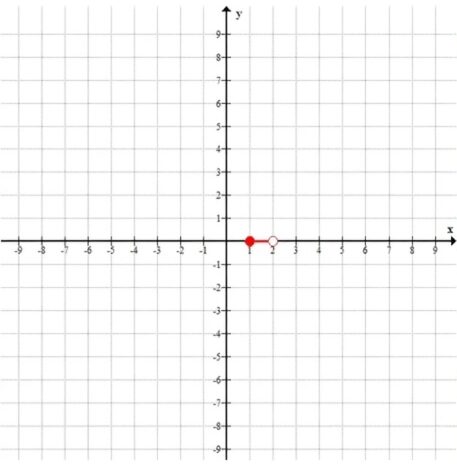
в) \( 1 \le x < 2, \; y = 0 \)
1. \(y = 0\) — ось \(OX\).
2. \(1 \le x < 2\) ⇒ отрезок на оси \(OX\) от \(x=1\) (включительно) до \(x=2\) (исключительно).
График: горизонтальный отрезок на оси \(y=0\) от \((1,0)\) до \((2,0)\), причём точка \((2,0)\) не входит (изображаем пустым кружком).
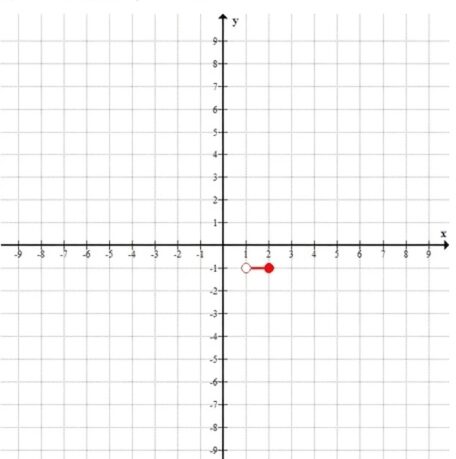
г) \( 1 \le x \le 2, \; y = -1 \)
Аналогично: горизонтальный отрезок на \(y=-1\) от \((1,-1)\) до \((2,-1)\), обе точки включены.
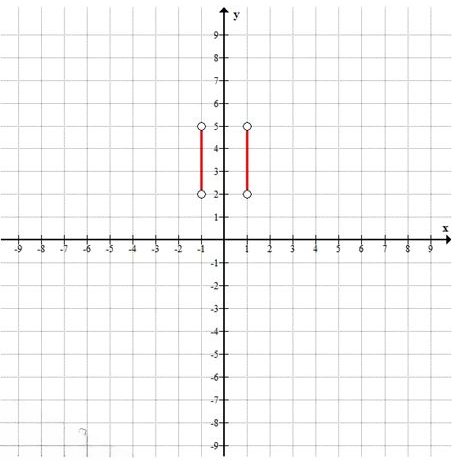
д)\( |x| = 1, \; 2 < y < 5 \)
1. \(|x| = 1\) ⇒ \(x = 1\) или \(x = -1\) — две вертикальные прямые.
2. \(2 < y < 5\) — горизонтальная полоса, но **y строго между 2 и 5.
3. Итог: на прямой \(x=1\) берём отрезок \(2 < y < 5\), на прямой \(x=-1\) берём отрезок \(2 < y < 5\). Границы \(y=2\) и \(y=5\) не включаются.
График: два вертикальных отрезка без концов.
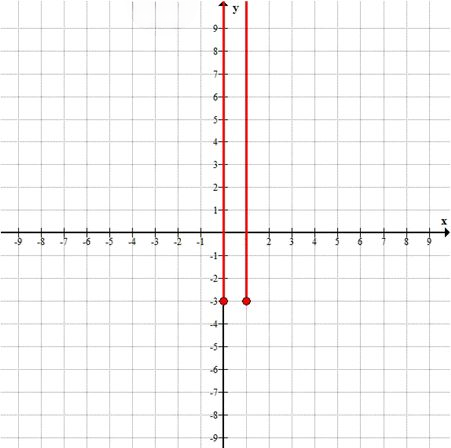
е) \( x(x-1) = 0, \; y \ge -3 \)
1. \(x(x-1)=0\) ⇒ \(x=0\) или \(x=1\) — две вертикальные прямые.
2. \(y \ge -3\) ⇒ включаем все точки на этих прямых с \(y\) не меньше \(-3\).
График: две вертикальные полупрямые:
— \(x=0, \; y \ge -3\)
— \(x=1, \; y \ge -3\)
Нижние точки \((0,-3)\) и \((1,-3)\) включены.
Итоговое описание графиков:
— а) две точки \((5,5)\) и \((5,-5)\)
— б) четыре точки: \((\pm3, \pm1)\)
— в) отрезок \([1,2)\) на оси \(y=0\)
— г) отрезок \([1,2]\) на \(y=-1\)
— д) два вертикальных открытых отрезка:
прямая \(x=1\) от \(y=2\) до \(y=5\), но без концов,
прямая \(x=-1\) аналогично.
— е) две вертикальные полупрямые от точек \((0,-3)\) и \((1,-3)\) вверх.