Учебное пособие «Алгебра, 7 класс» авторства Мордковича, Мардахаева и Семенова является важным ресурсом для школьников, желающих расширить свои знания в алгебре. Книга выделяется содержательной насыщенностью и продуманной методической организацией, что способствует более легкому и интересному освоению математического материала.
ГДЗ по Алгебре 7 Класс Глава 4 Дополнительная задача 9 Мордкович — Подробные Ответы
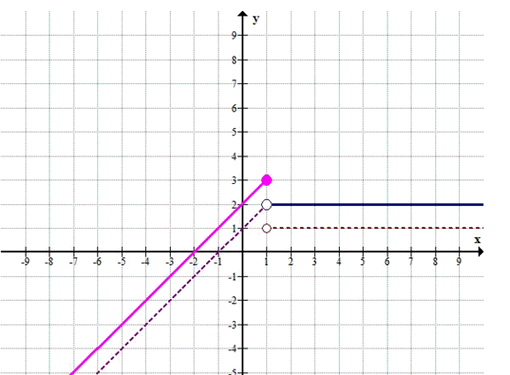
Дана функция у = s(x), где s(x) = {x + 1, x ≤ 1; 1, x > 1}. Постройте график функции: а) у = 1 + s(x); в) y = s(-x); б) у = s(х + 1); г) y = 2 — s(x).
a)
\(
y = 1 + s(x) =
\begin{cases}
1 + x + 1, & x \leq 1 \\
1 + 1, & x > 1
\end{cases}
=
\begin{cases}
x + 2, & x \leq 1 \\
2, & x > 1
\end{cases}
\)
б)
\(
y = s(x + 1) =
\begin{cases}
x + 1 + 1, & x + 1 \leq 1 \\
1, & x + 1 > 1
\end{cases}
=
\begin{cases}
x + 2, & x \leq 0 \\
1, & x > 0
\end{cases}
\)
в)
\(
y = s(-x) =
\begin{cases}
-x + 1, & -x \leq 1 \\
1, & -x > 1
\end{cases}
=
\begin{cases}
-x + 1, & x \geq -1 \\
1, & x < -1
\end{cases}
\)
г)
\(
y = 2 — s(x) =
\begin{cases}
2 — (x + 1), & x \leq 1 \\
2 — 1, & x > 1
\end{cases}
=
\begin{cases}
1 — x, & x \leq 1 \\
1, & x > 1
\end{cases}
\)
Условие:
Построить графики функций, используя \(s(x) = \begin{cases} x+1, & x \le 1 \\ 1, & x > 1 \end{cases}\):
а)
\(y = 1 + s(x)\);
б)
\(y = s(x+1)\);
в)
\(y = s(-x)\);
г)
\(y = 2 — s(x)\).
Решение:
а)
\(y = 1 + s(x)\)
\(s(x) = \begin{cases} x+1, & x \le 1 \\ 1, & x > 1 \end{cases}\)
— исходная функция
\(y = 1 + \begin{cases} x+1, & x \le 1 \\ 1, & x > 1 \end{cases}\)
— подставляем s(x)
\(y = \begin{cases} x+2, & x \le 1 \\ 2, & x > 1 \end{cases}\)
— упрощаем
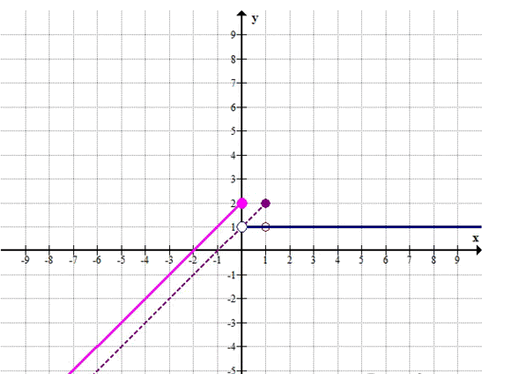
б)
\(y = s(x+1)\)
\(s(x+1) = \begin{cases} (x+1)+1, & x+1 \le 1 \\ 1, & x+1 > 1 \end{cases}\)
— замена x на x+1
\(s(x+1) = \begin{cases} x+2, & x \le 0 \\ 1, & x > 0 \end{cases}\)
— упрощаем
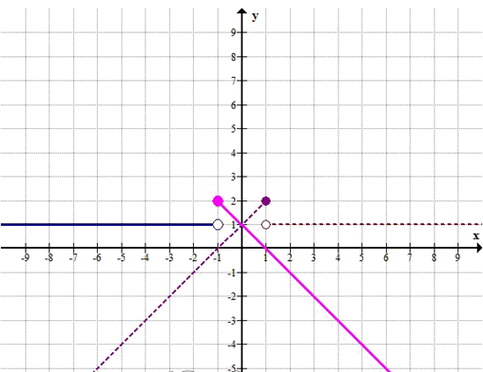
в)
\(y = s(-x)\)
\(s(-x) = \begin{cases} -x+1, & -x \le 1 \\ 1, & -x > 1 \end{cases}\)
— замена x на -x
\(s(-x) = \begin{cases} -x+1, & x \ge -1 \\ 1, & x < -1 \end{cases}\)
— упрощаем
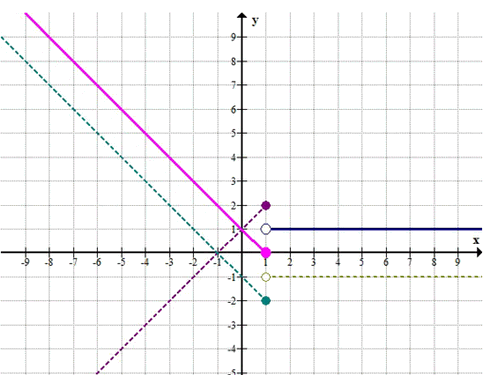
г)
\(y = 2 — s(x)\)
\(2 — s(x) = 2 — \begin{cases} x+1, & x \le 1 \\ 1, & x > 1 \end{cases}\)
— подставляем s(x)
\(2 — s(x) = \begin{cases} 2 — (x+1), & x \le 1 \\ 2 — 1, & x > 1 \end{cases}\)
— раскрываем скобки
\(2 — s(x) = \begin{cases} 1 — x, & x \le 1 \\ 1, & x > 1 \end{cases}\)
— упрощаем
а)
\(y = \begin{cases} x+2, & x \le 1 \\ 2, & x > 1 \end{cases}\)
б)
\(y = \begin{cases} x+2, & x \le 0 \\ 1, & x > 0 \end{cases}\)
в)
\(y = \begin{cases} -x+1, & x \ge -1 \\ 1, & x < -1 \end{cases}\)
г)
\(y = \begin{cases} 1 — x, & x \le 1 \\ 1, & x > 1 \end{cases}\)