Учебное пособие «Алгебра, 7 класс» авторства Мордковича, Мардахаева и Семенова является важным ресурсом для школьников, желающих расширить свои знания в алгебре. Книга выделяется содержательной насыщенностью и продуманной методической организацией, что способствует более легкому и интересному освоению математического материала.
ГДЗ по Алгебре 7 Класс Номер 12.12 Мордкович — Подробные Ответы
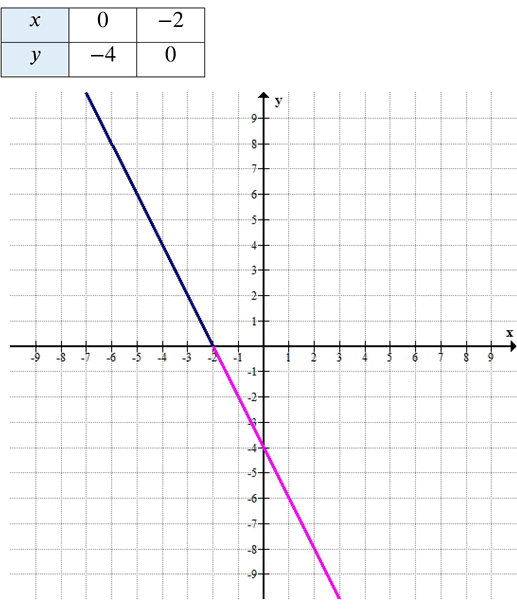
Постройте график линейной функции у = — 2х — 4. а) С помощью построенного графика решите уравнение —2х — 4 = 0. б) Выделите ту часть графика, которая соответствует условию у > О. Какие значения аргумента соответствуют выделенной части графика? в) С помощью графика решите неравенство — 2х — 4 > 0. г) Решите неравенство — 2х — 4 < 0.
y = –2x – 4;
а) –2x – 4 = 0, то есть, y = 0 при x = –2.
б) y > 0 — выделено синим цветом;
y > 0 при x < –2.
в) –2x – 4 > 0, то есть, y > 0 при x < –2.
г) –2x – 4 < 0, то есть, y < 0 при x > –2.
Рассмотрим линейную функцию y = –2x – 4. Для анализа этой функции построим её график и проанализируем поведение в различных диапазонах значений x.
Шаг 1. Построение таблицы значений
Для начала составим таблицу значений, чтобы понять, как функция ведёт себя при разных значениях x:
При x = 0, подставляем в уравнение:
y = –2 × 0 – 4 = –4.
При x = –2, подставляем в уравнение:
y = –2 × (–2) – 4 = 4 – 4 = 0.
Эти точки (0; –4 и –2; 0) помогут нам построить график функции.
Шаг 2. Анализ графика функции
График функции представляет собой прямую линию, которая убывает (так как коэффициент при x отрицательный, –2). Она пересекает ось Oy в точке (0; –4) и ось Ox в точке (–2; 0).
Шаг 3. Анализ значений функции
а) Нахождение нулей функции (y = 0)
Решаем уравнение:
–2x – 4 = 0
–2x = 4
x = –2.
Таким образом, y = 0 при x = –2. Это точка пересечения графика с осью Ox.
б) Определение интервалов, где y > 0 (выделено синим цветом на графике)
Функция y > 0, когда график находится выше оси Ox. Из графика видно, что это происходит при x < –2.
Вывод: y > 0 при x < –2.
в) Решение неравенства –2x – 4 > 0
Преобразуем неравенство:
–2x – 4 > 0
–2x > 4
x < –2 (при делении на отрицательное число знак неравенства меняется).
Это совпадает с предыдущим выводом: y > 0 при x < –2.
г) Решение неравенства –2x – 4 < 0
Преобразуем неравенство:
–2x – 4 < 0
–2x < 4
x > –2 (аналогично меняем знак неравенства).
Вывод: y < 0 при x > –2. Это соответствует части графика, которая находится ниже оси Ox.
Итог:
- Функция y = –2x – 4 убывает на всей области определения.
- Пересекает ось Ox в точке (–2; 0) и ось Oy в точке (0; –4).
- y > 0 при x < –2 (график выше оси Ox).
- y < 0 при x > –2 (график ниже оси Ox).
Если у вас есть дополнительные вопросы по этой теме — задавайте, с радостью помогу!