Учебное пособие «Алгебра, 7 класс» авторства Мордковича, Мардахаева и Семенова является важным ресурсом для школьников, желающих расширить свои знания в алгебре. Книга выделяется содержательной насыщенностью и продуманной методической организацией, что способствует более легкому и интересному освоению математического материала.
ГДЗ по Алгебре 7 Класс Номер 1.29 Мордкович — Подробные Ответы
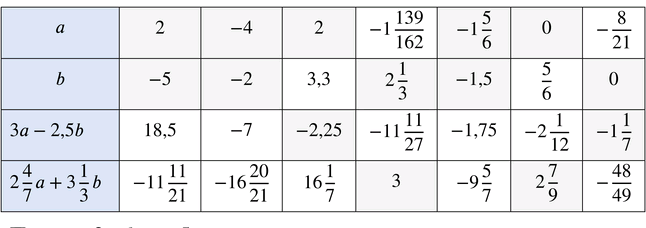
Заполните таблицу.
При \(a = 2\); \(b = -5\):
\[
3a — 2,5b = 3 \cdot 2 — 2,5 \cdot (-5) = 6 + 12,5 = 18,5;
\]
\[2\frac{4}{7}a + 3\frac{1}{3}b = 2\frac{4}{7} \cdot 2 + 3\frac{1}{3} \cdot (-5) = \frac{18}{7} \cdot 2 — \frac{10}{3} \cdot 5\]
\[= \frac{36}{7} — \frac{50}{3} = 5\frac{1}{7} — 16\frac{2}{3} = 5\frac{3}{21} — 16\frac{14}{21} = -11\frac{11}{21}.\]
При \(a = -4\); \(b = -2\):
\[
3a — 2,5b = 3 \cdot (-4) — 2,5 \cdot (-2) = -12 + 5 = -7;
\]
\[2\frac{4}{7}a + 3\frac{1}{3}b = 2\frac{4}{7} \cdot (-4) + 3\frac{1}{3} \cdot (-2) = \frac{18}{7} \cdot (-4) — \frac{10}{3} \cdot 2\]
\[= -\frac{72}{7} — \frac{20}{3} = -10\frac{2}{7} — 6\frac{2}{3} = -10\frac{6}{21} — 6\frac{14}{21} = -16\frac{20}{21}.\]
При \(a = 2\):
\[
3a — 2,5b = -2,25
\]
\[
3 \cdot 2 — 2,5b = -2,25
\]
\[
6 — 2,5b = -2,25
\]
\[
2,5b = 6 + 2,25
\]
\[
2,5b = 8,25
\]
\[
b = 8,25 : 2,5
\]
\[
b = 3,3.
\]
Тогда:
\[2\frac{4}{7}a + 3\frac{1}{3}b = 2\frac{4}{7} \cdot 2 + 3\frac{1}{3} \cdot 3,3\]
\[= \frac{18}{7} \cdot 2 + \frac{10}{3} \cdot \frac{33}{10}= \frac{36}{7} + 11 = 5\frac{1}{7} + 11 = 16\frac{1}{7}\]
При \(b = 2\frac{1}{3}\):
\[
2\frac{4}{7}a + 3\frac{1}{3}b = 3
\]
\[
2\frac{4}{7}a + \frac{10}{3} \cdot \frac{7}{3} = 3
\]
\[
2\frac{4}{7}a + \frac{70}{9} = 3
\]
\[
2\frac{4}{7}a = 3 — 7\frac{7}{9}
\]
\[
2\frac{4}{7}a = -4\frac{7}{9}
\]
\[
a = -4\frac{7}{9} : 2\frac{4}{7}
\]
\[
a = -\frac{43}{9} : \frac{18}{7}
\]
\[
a = -\frac{43 \cdot 7}{9 \cdot 18}
\]
\[
a = -\frac{301}{162}
\]
\[
a = -1\frac{139}{162}.
\]
Тогда:
\[
3a — 2,5b = 3 \cdot \left(-\frac{301}{162}\right) — 2,5 \cdot 2\frac{1}{3} = -\frac{301}{54} — \frac{5}{2} \cdot \frac{7}{3} =
\]
\[
= -5\frac{31}{54} — \frac{35}{6} = -5\frac{31}{54} — 5\frac{5}{6} = -5\frac{31}{54} — 5\frac{45}{54} = -10\frac{76}{54} =
\]
\[
= -11\frac{22}{54} = -11\frac{11}{27}.
\]
При \(a = -1\frac{5}{6}\); \(b = -1,5\):
\[
3a — 2,5b = 3 \cdot \left(-1\frac{5}{6}\right) — 2,5 \cdot (-1,5) = 3 \cdot \left(-\frac{11}{6}\right) + 3,75 =
\]
\[
= -\frac{11}{2} + 3,75 = -5,5 + 3,75 = -1,75;
\]
\[
2\frac{4}{7}a+3\frac{1}{3}b=2\frac{4}{7} \cdot \left(-1\frac{5}{6}\right) + 3\frac{1}{3} \cdot (-1,5) = \frac{18}{7} \cdot \left(-\frac{11}{6}\right) — \frac{10}{3} \cdot \frac{3}{2} \]
\[
= -\frac{18 \cdot 11}{7 \cdot 6} — 5 = -\frac{3 \cdot 11}{7 \cdot 1} — 5 = -\frac{33}{7} — 5 = -4\frac{5}{7} — 5 = -9\frac{5}{7}.
\]
При \(a = 0\):
\[
2\frac{4}{7}a + 3\frac{1}{3}b = 2\frac{7}{9}
\]
\[
2\frac{4}{7} \cdot 0 + 3\frac{1}{3}b = 2\frac{7}{9}
\]
\[
3\frac{1}{3}b = 2\frac{7}{9}
\]
\[
b = 2\frac{7}{9} : 3\frac{1}{3}
\]
\[
b = \frac{25}{9} : \frac{10}{3}
\]
\[
b = \frac{25 \cdot 3}{9 \cdot 10}
\]
\[
b = \frac{5 \cdot 1}{3 \cdot 2}
\]
\[
b = \frac{5}{6}.
\]
Тогда:
\[
3a — 2,5b = 3 \cdot 0 — 2,5 \cdot \frac{5}{6} = 0 — \frac{5}{2} \cdot \frac{5}{6} = -\frac{25}{12} = -2\frac{1}{12}.
\]
При \(b = 0\):
\[
3a — 2,5b = -1\frac{1}{7}
\]
\[
3a — 2,5 \cdot 0 = -\frac{8}{7}
\]
\[
3a = -\frac{8}{7}
\]
\[
a = -\frac{8}{7} : 3
\]
\[
a = -\frac{8}{7} \cdot \frac{1}{3}
\]
\[
a = -\frac{8}{21}.
\]
Тогда:
\[
2\frac{4}{7}a + 3\frac{1}{3}b = 2\frac{4}{7} \cdot \left(-\frac{8}{21}\right) + 3\frac{1}{3} \cdot 0 = \frac{18}{7} \cdot \left(-\frac{8}{21}\right) + 0 =
\]
\[
= -\frac{18 \cdot 8}{7 \cdot 21} = -\frac{6 \cdot 8}{7 \cdot 7} = -\frac{48}{49}.
\]
1. Случай: \(a = 2\), \(b = -5\)
Вычислим значение выражения \(3a — 2{,}5b\):
\[
3a — 2{,}5b = 3 \cdot 2 — 2{,}5 \cdot (-5)
\]
\[
= 6 — (-12{,}5)
\]
\[
= 6 + 12{,}5
\]
\[
= 18{,}5
\]
Теперь вычислим значение выражения \(2\frac{4}{7}a + 3\frac{1}{3}b\).
Сначала переведём смешанные числа в неправильные дроби:
\[
2\frac{4}{7} = \frac{2 \cdot 7 + 4}{7} = \frac{14 + 4}{7} = \frac{18}{7}
\]
\[
3\frac{1}{3} = \frac{3 \cdot 3 + 1}{3} = \frac{9 + 1}{3} = \frac{10}{3}
\]
Подставляем значения:
\[
2\frac{4}{7}a + 3\frac{1}{3}b = \frac{18}{7} \cdot 2 + \frac{10}{3} \cdot (-5)
\]
\[
= \frac{36}{7} — \frac{50}{3}
\]
Приведём дроби к общему знаменателю. Наименьшее общее кратное чисел 7 и 3 — это 21:
\[
\frac{36}{7} = \frac{36 \cdot 3}{21} = \frac{108}{21}, \quad \frac{50}{3} = \frac{50 \cdot 7}{21} = \frac{350}{21}
\]
\[
\frac{108}{21} — \frac{350}{21} = \frac{-242}{21}
\]
Переведём неправильную дробь в смешанное число:
\[
242 \div 21 = 11 \text{ (остаток } 11\text{)}, \quad \text{поэтому } \frac{-242}{21} = -11\frac{11}{21}
\]
Итак:
\[
2\frac{4}{7}a + 3\frac{1}{3}b = -11\frac{11}{21}
\]
2. Случай: \(a = -4\), \(b = -2\)
Вычислим \(3a — 2{,}5b\):
\[
3a — 2{,}5b = 3 \cdot (-4) — 2{,}5 \cdot (-2)
\]
\[
= -12 — (-5)
\]
\[
= -12 + 5
\]
\[
= -7
\]
Теперь вычислим \(2\frac{4}{7}a + 3\frac{1}{3}b\):
\[
= \frac{18}{7} \cdot (-4) + \frac{10}{3} \cdot (-2)
\]
\[
= -\frac{72}{7} — \frac{20}{3}
\]
Приведём к общему знаменателю 21:
\[
-\frac{72}{7} = -\frac{216}{21}, \quad -\frac{20}{3} = -\frac{140}{21}
\]
\[
-\frac{216}{21} — \frac{140}{21} = -\frac{356}{21}
\]
Разделим 356 на 21: \(21 \cdot 16 = 336\), остаток 20 → \(356 = 21 \cdot 16 + 20\)
\[
-\frac{356}{21} = -16\frac{20}{21}
\]
3. Случай: \(a = 2\), значение \(3a — 2{,}5b = -2{,}25\)
Найдём \(b\):
\[
3a — 2{,}5b = -2{,}25
\]
\[
3 \cdot 2 — 2{,}5b = -2{,}25
\]
\[
6 — 2{,}5b = -2{,}25
\]
Переносим 6 в правую часть:
\[
-2{,}5b = -2{,}25 — 6
\]
\[
-2{,}5b = -8{,}25
\]
Умножим обе части на \(-1\):
\[
2{,}5b = 8{,}25
\]
Разделим:
\[
b = \frac{8{,}25}{2{,}5} = \frac{825}{250} = \frac{33}{10} = 3{,}3
\]
Теперь вычислим второе выражение:
\[
2\frac{4}{7}a + 3\frac{1}{3}b = \frac{18}{7} \cdot 2 + \frac{10}{3} \cdot 3{,}3
\]
Заметим, что \(3{,}3 = \frac{33}{10}\), поэтому:
\[
\frac{10}{3} \cdot \frac{33}{10} = \frac{33}{3} = 11
\]
\[
\frac{18}{7} \cdot 2 = \frac{36}{7} = 5\frac{1}{7}
\]
\[
5\frac{1}{7} + 11 = 16\frac{1}{7}
\]
4. Случай: \(b = 2\frac{1}{3}\), значение \(2\frac{4}{7}a + 3\frac{1}{3}b = 3\)
Переведём \(b = 2\frac{1}{3} = \frac{7}{3}\)
\[
3\frac{1}{3}b = \frac{10}{3} \cdot \frac{7}{3} = \frac{70}{9}
\]
Подставим в уравнение:
\[
2\frac{4}{7}a + \frac{70}{9} = 3
\]
\[
2\frac{4}{7}a = 3 — \frac{70}{9} = \frac{27}{9} — \frac{70}{9} = -\frac{43}{9}
\]
\[
2\frac{4}{7} = \frac{18}{7}, \quad \text{поэтому } \frac{18}{7}a = -\frac{43}{9}
\]
Решаем уравнение:
\[
a = -\frac{43}{9} : \frac{18}{7} = -\frac{43}{9} \cdot \frac{7}{18} = -\frac{301}{162}
\]
Переведём в смешанное число:
\[
301 \div 162 = 1 \text{ (остаток } 139\text{)} \Rightarrow a = -1\frac{139}{162}
\]
Теперь найдём \(3a — 2{,}5b\):
\[
3a = 3 \cdot \left(-\frac{301}{162}\right) = -\frac{903}{162} = -\frac{301}{54}
\]
\[
2{,}5b = \frac{5}{2} \cdot \frac{7}{3} = \frac{35}{6}
\]
\[
3a — 2{,}5b = -\frac{301}{54} — \frac{35}{6}
\]
Приведём к общему знаменателю 54:
\[
\frac{35}{6} = \frac{315}{54}
\]
\[
-\frac{301}{54} — \frac{315}{54} = -\frac{616}{54} = -\frac{308}{27}
\]
Разделим: \(308 \div 27 = 11\) (остаток 11), так как \(27 \cdot 11 = 297\), \(308 — 297 = 11\)
\[
-\frac{308}{27} = -11\frac{11}{27}
\]
5. Случай: \(a = -1\frac{5}{6}\), \(b = -1{,}5\)
Переведём:
\[
a = -\frac{11}{6}, \quad b = -\frac{3}{2}
\]
Вычислим \(3a — 2{,}5b\):
\[
3a = 3 \cdot \left(-\frac{11}{6}\right) = -\frac{33}{6} = -\frac{11}{2} = -5{,}5
\]
\[
2{,}5b = \frac{5}{2} \cdot \left(-\frac{3}{2}\right) = -\frac{15}{4} = -3{,}75
\]
\[
3a — 2{,}5b = -5{,}5 — (-3{,}75) = -5{,}5 + 3{,}75 = -1{,}75
\]
Теперь второе выражение:
\[
2\frac{4}{7}a = \frac{18}{7} \cdot \left(-\frac{11}{6}\right) = -\frac{198}{42} = -\frac{33}{7}
\]
\[
3\frac{1}{3}b = \frac{10}{3} \cdot \left(-\frac{3}{2}\right) = -\frac{30}{6} = -5
\]
\[
-\frac{33}{7} — 5 = -\frac{33}{7} — \frac{35}{7} = -\frac{68}{7} = -9\frac{5}{7}
\]
6. Случай: \(a = 0\), значение \(2\frac{4}{7}a + 3\frac{1}{3}b = 2\frac{7}{9}\)
Поскольку \(a = 0\), первое слагаемое равно нулю:
\[
3\frac{1}{3}b = 2\frac{7}{9}
\]
\[
\frac{10}{3}b = \frac{25}{9}
\]
\[
b = \frac{25}{9} : \frac{10}{3} = \frac{25}{9} \cdot \frac{3}{10} = \frac{75}{90} = \frac{5}{6}
\]
Теперь:
\[
3a — 2{,}5b = 0 — \frac{5}{2} \cdot \frac{5}{6} = -\frac{25}{12} = -2\frac{1}{12}
\]
7. Случай: \(b = 0\), значение \(3a — 2{,}5b = -1\frac{1}{7}\)
\[
3a = -\frac{8}{7}
\]
\[
a = -\frac{8}{7} \cdot \frac{1}{3} = -\frac{8}{21}
\]
Теперь:
\[
2\frac{4}{7}a = \frac{18}{7} \cdot \left(-\frac{8}{21}\right) = -\frac{144}{147} = -\frac{48}{49}
\]
(сократили на 3)
Второе слагаемое равно нулю, так как \(b = 0\).
Итог: \(-\frac{48}{49}\)