Учебное пособие «Алгебра, 7 класс» авторства Мордковича, Мардахаева и Семенова является важным ресурсом для школьников, желающих расширить свои знания в алгебре. Книга выделяется содержательной насыщенностью и продуманной методической организацией, что способствует более легкому и интересному освоению математического материала.
ГДЗ по Алгебре 7 Класс Номер 11.10 Мордкович — Подробные Ответы
Используя две переменные х и у, составьте математическую модель ситуации и выполните решение графическим способом. Найдите два числа, если известно, что их сумма равна 12, а разность 2.
\(
\begin{cases}
x + y = 12 \\
x — y = 2
\end{cases}
\)
\(
y = 12 — x
\)
\(
y = x — 2
\)
\(
\begin{array}{c|c}
x & y = 12 — x \\
\hline
5 & 7 \\
6 & 6 \\
7 & 5
\end{array}
\)
\(
\begin{array}{c|c}
x & y = x — 2 \\
\hline
5 & 3 \\
6 & 4 \\
7 & 5
\end{array}
\)
\(
\begin{cases}
x = 7 \\
y = 5
\end{cases}
\)
Условие:
Найти два числа, сумма которых равна 12, а разность — 2, используя математическую модель с двумя переменными и графический метод.
Решение:
Пусть \( x \) и \( y \) — искомые числа.
По условию:
— Сумма чисел:
\( x + y = 12 \)
— Разность чисел:
\( x — y = 2 \)
Получили систему уравнений:
\[
\begin{cases}
x + y = 12 \\
x — y = 2
\end{cases}
\]
Выразим \( y \) через \( x \) из каждого уравнения:
Из первого уравнения:
\( y = 12 — x \)
Из второго уравнения:
\( y = x — 2 \)
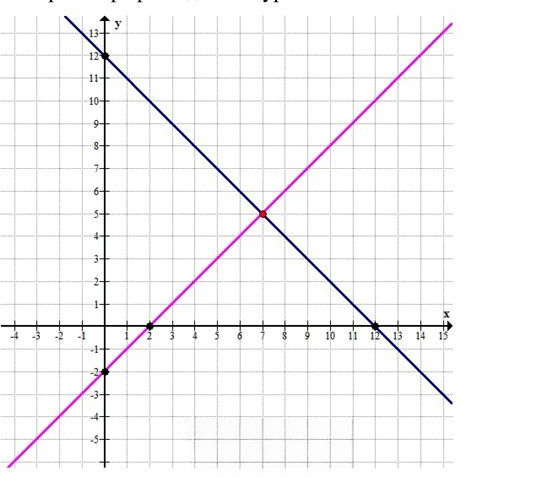
Графики функций:
Каждое уравнение задаёт прямую линию.
1) Прямая \( y = 12 — x \):
— При \( x = 0 \): \( y = 12 \) → точка \( (0; 12) \)
— При \( x = 12 \): \( y = 0 \) → точка \( (12; 0) \)
2) Прямая \( y = x — 2 \):
— При \( x = 0 \): \( y = -2 \) → точка \( (0; -2) \)
— При \( x = 2 \): \( y = 0 \) → точка \( (2; 0) \)
Точка пересечения:
Решим систему алгебраически:
Сложим уравнения:
\( (x + y) + (x — y) = 12 + 2 \)
\( 2x = 14 \)
\( x = 7 \)
Подставим \( x = 7 \) в первое уравнение:
\( 7 + y = 12 \)
\( y = 5 \)
Ответ:
\( x = 7 \), \( y = 5 \)