Учебное пособие «Алгебра, 7 класс» авторства Мордковича, Мардахаева и Семенова является важным ресурсом для школьников, желающих расширить свои знания в алгебре. Книга выделяется содержательной насыщенностью и продуманной методической организацией, что способствует более легкому и интересному освоению математического материала.
ГДЗ по Алгебре 7 Класс Номер 11.11 Мордкович — Подробные Ответы
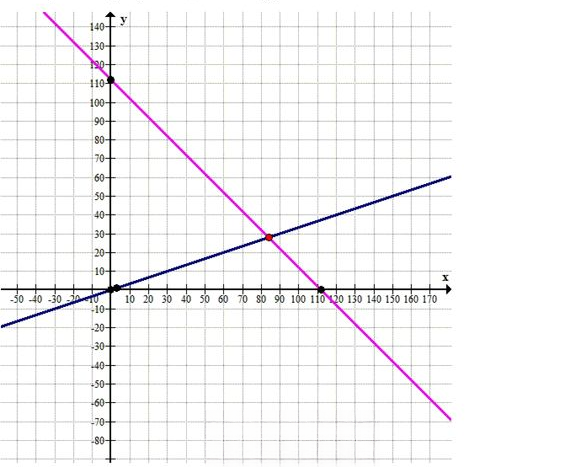
Используя две переменные х и у, составьте математическую модель ситуации и выполните решение графическим способом. Одно число больше другого в 3 раза. Найдите эти числа, если известно, что их сумма равна 112.
\( x = 3y \)
\( x + y = 112 \)
1)
\( 3y + y = 112 \)
\( 4y = 112 \)
\( y = \frac{112}{4} \)
\( y = 28 \)
\( x = 3 \cdot 28 \)
\( x = 84 \)
Условие задачи:
Найти два числа, если их сумма равна 112, а одно из них в 3 раза больше другого.
I этап. Составление математической модели
Обозначим искомые числа:
— Пусть \( x \) — меньшее число (это удобно, так как второе число выражается через него как «в 3 раза больше»).
— Тогда большее число в три раза превышает меньшее, то есть оно равно \( 3x \).
Теперь переведём условия задачи на язык математики.
1. «Одно число в 3 раза больше другого» → \( y = 3x \), где \( y \) — большее число.
Это даёт первое уравнение:
\[
y = 3x
\]
2. «Их сумма равна 112» → \( x + y = 112 \).
Это даёт второе уравнение:
\[
x + y = 112
\]
Объединяя их, получаем систему двух линейных уравнений с двумя переменными:
\[
\begin{cases}
y = 3x \\
x + y = 112
\end{cases}
\]
II этап. Работа с математической моделью
Подставим выражение для \( y \) из первого уравнения во второе:
\[
x + (3x) = 112
\]
Упростим левую часть, объединяя подобные слагаемые:
\[
4x = 112
\]
Решим полученное уравнение относительно \( x \). Для этого разделим обе части уравнения на 4:
\[
x = \frac{112}{4}
\]
Выполним деление:
\[
x = 28
\]
Таким образом, меньшее число равно \( 28 \).
Найдём большее число, подставив найденное значение \( x = 28 \) в выражение \( y = 3x \):
\[
y = 3 \cdot 28
\]
\[
y = 84
\]
Итак, второе число равно \( 84 \).
III этап. Интерпретация и проверка результата
Мы получили два числа: \( 28 \) и \( 84 \).
Проверим, удовлетворяют ли они условиям задачи.
1.Проверка суммы:
\( 28 + 84 = 112 \) — условие выполнено.
2.Проверка кратности:
\( 84 \div 28 = 3 \) → число \( 84 \) действительно в 3 раза больше числа \( 28 \) — условие также выполнено.
Оба условия задачи соблюдены, значит, решение найдено верно.
Ответ: меньшее число — \( 28 \), большее число — \( 84 \).