ГДЗ по Алгебре 7 Класс Номер 11.12 Мордкович — Подробные Ответы

Используя две переменные х и у, составьте математическую модель ситуации и выполните решение графическим способом. В создании проекта участвовало 14 учащихся. При этом девочек оказалось в 2,5 раза больше, чем мальчиков. Сколько мальчиков и сколько девочек участвовало в создании проекта?

Пусть в создании проекта участвовало \( x \) девочек и \( y \) мальчиков.
Всего было 14 учащихся, значит, \( x + y = 14 \).
При этом девочек оказалось в 2,5 раза больше, чем мальчиков, значит, \( x = 2{,}5y \).

Составим систему уравнений:
\[
\begin{cases}
x + y = 14 \\
x = 2{,}5y
\end{cases}
\]

\( x + y = 14 \)

Если \( x = 0 \), то:
\( 0 + y = 14 \)
\( y = 14 \Longrightarrow (0; 14) \) — точка графика.

Если \( y = 0 \), то:
\( x + 0 = 14 \)
\( x = 14 \Longrightarrow (14; 0) \) — точка графика.

\( x = 2{,}5y \)

Если \( x = 0 \), то:
\( 0 = 2{,}5y \)
\( y = 0 \Longrightarrow (0; 0) \) — точка графика.

Если \( x = 5 \), то:
\( 5 = 2{,}5y \)
\( y = 2 \Longrightarrow (5; 2) \) — точка графика.

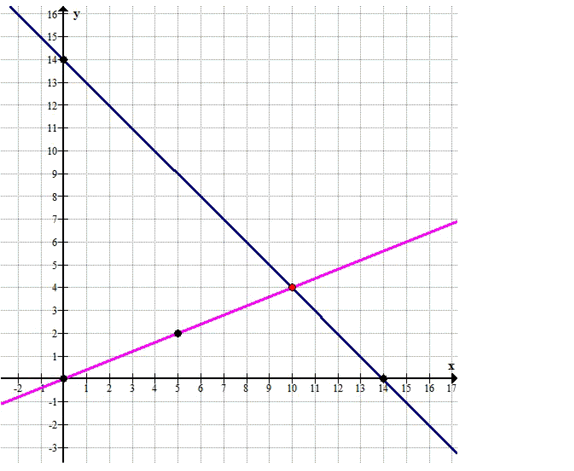
Построим графики данных уравнений:

Прямые пересекаются в точке \( (10; 4) \), значит, \( x = 10 \), \( y = 4 \).

Таким образом, в создании проекта участвовало 4 мальчика и 10 девочек.

Ответ: 4 мальчика и 10 девочек.

I этап. Составление математической модели

Обозначим:

— Пусть \( x \) — количество девочек,
— Пусть \( y \) — количество мальчиков.

По условию:

1. Всего учащихся — 14:
\[
x + y = 14
\]

2. Девочек в 2,5 раза больше, чем мальчиков:
\[
x = 2{,}5y
\]

Таким образом, получаем систему двух уравнений с двумя неизвестными:
\[
\begin{cases}
x + y = 14 \\
x = 2{,}5y
\end{cases}
\]

Эта система описывает зависимость между количеством девочек и мальчиков. Решение системы даст нам точное число участников каждого пола.

II этап. Работа с моделью — построение графиков

Каждое уравнение системы задаёт прямую на координатной плоскости \( (x; y) \). Найдём по две точки для построения каждой прямой.

1. Прямая: \( x + y = 14 \)

Это линейное уравнение. Найдём точки пересечения с осями.

— Если \( x = 0 \):
\( 0 + y = 14 \) → \( y = 14 \) → точка \( (0; 14) \)

— Если \( y = 0 \):
\( x + 0 = 14 \) → \( x = 14 \) → точка \( (14; 0) \)

Эти две точки позволяют провести прямую — она проходит через \( (0; 14) \) и \( (14; 0) \), и имеет отрицательный наклон.

2. Прямая: \( x = 2{,}5y \)

Это уравнение уже выражает \( x \) через \( y \). Найдём две точки:

— Если \( y = 0 \):
\( x = 2{,}5 \cdot 0 = 0 \) → точка \( (0; 0) \)

— Если \( y = 2 \):
\( x = 2{,}5 \cdot 2 = 5 \) → точка \( (5; 2) \)

Можно проверить ещё одну точку для уверенности:

— Если \( y = 4 \):
\( x = 2{,}5 \cdot 4 = 10 \) → точка \( (10; 4) \)

Эта прямая проходит через начало координат и имеет положительный наклон.

III этап. Нахождение точки пересечения

Графически — прямые пересекаются в одной точке, координаты которой и дают решение системы.

Из построения видно, что прямая \( x = 2{,}5y \) проходит через точку \( (10; 4) \), и проверим, удовлетворяет ли она первому уравнению:

Подставим \( x = 10 \), \( y = 4 \) в \( x + y = 14 \):
\( 10 + 4 = 14 \) → верно.

Значит, точка \( (10; 4) \) — точка пересечения прямых.

Следовательно, решение системы:
\( x = 10 \), \( y = 4 \)

IV этап. Интерпретация результата

— \( x = 10 \) — количество девочек
— \( y = 4 \) — количество мальчиков

Проверим соответствие условиям задачи:

1. Общее количество:
\( 10 + 4 = 14 \) — верно.

2. Соотношение:
\( 10 : 4 = 2{,}5 \) → девочек в 2,5 раза больше, чем мальчиков — верно.

Ответ:
В создании проекта участвовало 10 девочек и 4 мальчика.