ГДЗ по Алгебре 7 Класс Номер 11.13 Мордкович — Подробные Ответы

Используя две переменные х и у, составьте математическую модель ситуации и выполните решение графическим способом. На школьном участке учащиеся посадили липы и клёны. При этом лип было посажено в 3 раза меньше, чем клёнов. Сколько деревьев посадили учащиеся, если клёнов оказалось на 10 деревьев больше, чем лип?

Пусть учащиеся посадили \( x \) лип и \( y \) кленов.

Так как лип было посажено в 3 раза меньше, чем кленов, то \( 3x = y \).

Известно, что кленов на 10 деревьев больше, чем лип, значит, \( y — x = 10 \).

Составим систему уравнений:
\[
\begin{cases}
3x = y \\
y — x = 10
\end{cases}
\]

\( 3x = y \)

Если \( x = 0 \), то:
\( 3 \cdot 0 = y \)
\( y = 0 \Longrightarrow (0; 0) \) — точка графика.

Если \( x = 1 \), то:
\( 3 \cdot 1 = y \)
\( y = 3 \Longrightarrow (1; 3) \) — точка графика.

\( y — x = 10 \)

Если \( x = 0 \), то:
\( y — 0 = 10 \)
\( y = 10 \Longrightarrow (0; 10) \) — точка графика.

Если \( y = 0 \), то:
\( 0 — x = 10 \)
\( -x = 10 \)
\( x = -10 \Longrightarrow (-10; 0) \) — точка графика.

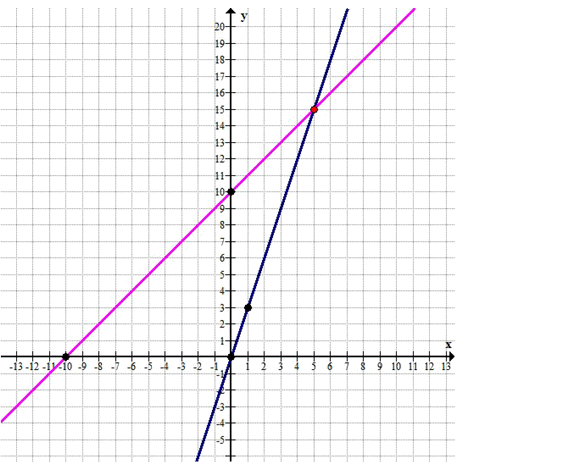
Построим графики данных уравнений:

Прямые пересекаются в точке \( (5; 15) \), значит, \( x = 5 \), \( y = 15 \).

Таким образом, учащиеся посадили 5 лип и 15 кленов.

Всего они посадили:
\( 5 + 15 = 20 \) (деревьев).

Ответ: 20 деревьев.

I этап. Составление математической модели

Обозначим:

— \( x \) — количество посаженных лип,
— \( y \) — количество посаженных клёнов.

Переведём условия задачи в математические уравнения.

1. «Лип посадили в 3 раза меньше, чем клёнов» означает, что клёнов в 3 раза больше, чем лип.
Это можно записать как:
\[
y = 3x \quad \text{или} \quad 3x = y
\]

2. «Клёнов на 10 деревьев больше, чем лип» означает:
\[
y — x = 10
\]

Таким образом, получаем систему двух линейных уравнений с двумя переменными:
\[
\begin{cases}
3x = y \\
y — x = 10
\end{cases}
\]

II этап. Работа с моделью — построение графиков

Каждое уравнение системы задаёт прямую на координатной плоскости. Найдём по две точки для построения каждой прямой.

Уравнение 1: \( 3x = y \)

Это уравнение можно записать как \( y = 3x \). Это прямая, проходящая через начало координат.

— При \( x = 0 \):
\( y = 3 \cdot 0 = 0 \) → точка \( (0; 0) \)

— При \( x = 1 \):
\( y = 3 \cdot 1 = 3 \) → точка \( (1; 3) \)

Можно также взять \( x = 5 \):
\( y = 3 \cdot 5 = 15 \) → точка \( (5; 15) \)

Уравнение 2: \( y — x = 10 \)

Преобразуем к виду \( y = x + 10 \)

— При \( x = 0 \):
\( y = 0 + 10 = 10 \) → точка \( (0; 10) \)

— При \( y = 0 \):
\( 0 = x + 10 \) → \( x = -10 \) → точка \( (-10; 0) \)

Можно также проверить \( x = 5 \):
\( y = 5 + 10 = 15 \) → точка \( (5; 15) \)

III этап. Нахождение точки пересечения графиков

Графически — точка пересечения двух прямых и есть решение системы.

Из вычислений видно, что обе прямые проходят через точку \( (5; 15) \):

— Для первой прямой: \( y = 3x = 3 \cdot 5 = 15 \)
— Для второй прямой: \( y = x + 10 = 5 + 10 = 15 \)

Следовательно, координаты точки пересечения:
\[
x = 5, \quad y = 15
\]

IV этап. Интерпретация результата

— \( x = 5 \) — количество лип,
— \( y = 15 \) — количество клёнов.

Проверка условий:

1. Лип в 3 раза меньше, чем клёнов:
\( 15 : 5 = 3 \) — верно.

2. Клёнов на 10 больше, чем лип:
\( 15 — 5 = 10 \) — верно.

Оба условия выполнены.

Найдём общее количество посаженных деревьев:
\[
5 + 15 = 20
\]

Ответ: учащиеся посадили 20 деревьев.