Учебное пособие «Алгебра, 7 класс» авторства Мордковича, Мардахаева и Семенова является важным ресурсом для школьников, желающих расширить свои знания в алгебре. Книга выделяется содержательной насыщенностью и продуманной методической организацией, что способствует более легкому и интересному освоению математического материала.
ГДЗ по Алгебре 7 Класс Номер 11.3 Мордкович — Подробные Ответы
Постройте график линейного уравнения в системе координат tOs: а) 2t + s = 0; в) 3t + 2s = —6; б) t — s = 2; г) t + 2s — 3 = 0.
а) \( 2t + s = 0 \)
Если \( t = 0 \), то:
\( 2 \cdot 0 + s = 0 \)
\( s = 0 \) ⟹ \( (0; 0) \) — точка графика.
Если \( t = 1 \), то:
\( 2 \cdot 1 + s = 0 \)
\( 2 + s = 0 \)
\( s = -2 \) ⟹ \( (1; -2) \) — точка графика.
б) \( t — s = 2 \)
Если \( t = 0 \), то:
\( 0 — s = 2 \)
\( -s = 2 \)
\( s = -2 \) ⟹ \( (0; -2) \) — точка графика.
Если \( s = 0 \), то:
\( t — 0 = 2 \)
\( t = 2 \) ⟹ \( (2; 0) \) — точка графика.
в) \( 3t + 2s = -6 \)
Если \( t = 0 \), то:
\( 3 \cdot 0 + 2s = -6 \)
\( 2s = -6 \)
\( s = -3 \) ⟹ \( (0; -3) \) — точка графика.
Если \( s = 0 \), то:
\( 3t + 2 \cdot 0 = -6 \)
\( 3t = -6 \)
\( t = -2 \) ⟹ \( (-2; 0) \) — точка графика.
г) \( t + 2s — 3 = 0 \)
Если \( t = 0 \), то:
\( 0 + 2s — 3 = 0 \)
\( 2s = 3 \)
\( s = 1{,}5 \) ⟹ \( (0; 1{,}5) \) — точка графика.
Если \( s = 0 \), то:
\( t + 2 \cdot 0 — 3 = 0 \)
\( t — 3 = 0 \)
\( t = 3 \) ⟹ \( (3; 0) \) — точка графика.
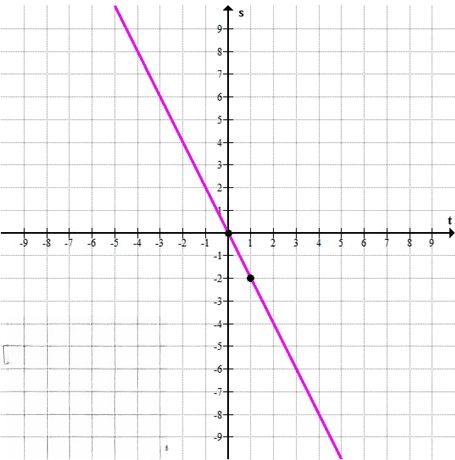
а)Уравнение: \( 2t + s = 0 \)
Найдём точки пересечения графика с осями координат.
Если \( t = 0 \):
Подставим:
\( 2 \cdot 0 + s = 0 \)
\( s = 0 \)
Получаем точку: \( (0; 0) \) — начало координат.
Если \( t = 1 \):
Подставим:
\( 2 \cdot 1 + s = 0 \)
\( 2 + s = 0 \)
\( s = -2 \)
Получаем точку: \( (1; -2) \)
Эти две точки определяют прямую, проходящую через начало координат и наклонённую вниз направо.
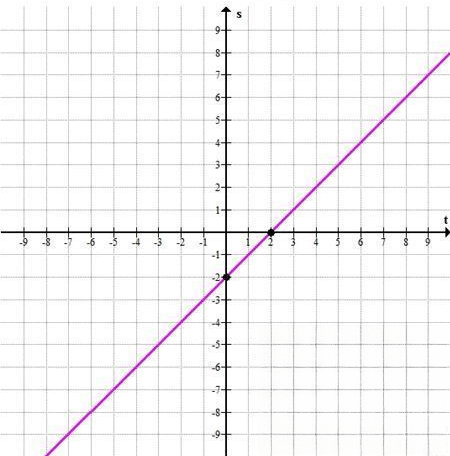
б) Уравнение: \( t — s = 2 \)
Перепишем:
\( t — s = 2 \)
Если \( t = 0 \):
Подставим:
\( 0 — s = 2 \)
\( -s = 2 \)
Умножим обе части на -1:
\( s = -2 \)
Получаем точку: \( (0; -2) \)
Если \( s = 0 \):
Подставим:
\( t — 0 = 2 \)
\( t = 2 \)
Получаем точку: \( (2; 0) \)
График — прямая, проходящая через эти две точки, наклонённая вверх направо.
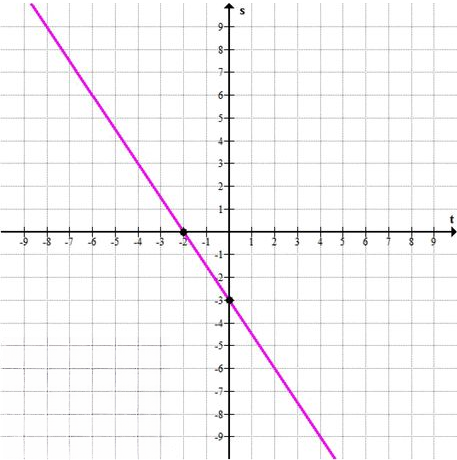
в) Уравнение: \( 3t + 2s = -6 \)
Найдём точки пересечения графика с осями координат.
Если \( t = 0 \):
Подставим в уравнение:
\( 3 \cdot 0 + 2s = -6 \)
\( 0 + 2s = -6 \)
\( 2s = -6 \)
Разделим обе части на 2:
\( s = \frac{-6}{2} \)
\( s = -3 \)
Получаем точку: \( (0; -3) \) — это точка пересечения с осью \( s \).
Если \( s = 0 \):
Подставим в уравнение:
\( 3t + 2 \cdot 0 = -6 \)
\( 3t = -6 \)
Разделим обе части на 3:
\( t = \frac{-6}{3} \)
\( t = -2 \)
Получаем точку: \( (-2; 0) \) — это точка пересечения с осью \( t \).
На графике эти две точки соединяются прямой линией, которая является графиком данного уравнения.
г) Уравнение: \( t + 2s — 3 = 0 \)
Перепишем в виде:
\( t + 2s = 3 \)
Если \( t = 0 \):
Подставим:
\( 0 + 2s = 3 \)
\( 2s = 3 \)
Разделим на 2:
\( s = \frac{3}{2} = 1{,}5 \)
Получаем точку: \( (0; 1{,}5) \)
Если \( s = 0 \):
Подставим:
\( t + 2 \cdot 0 = 3 \)
\( t = 3 \)
Получаем точку: \( (3; 0) \)
График — прямая, проходящая через эти две точки, пересекает ось \( s \) выше нуля и ось \( t \) справа от начала координат.