ГДЗ по Алгебре 7 Класс Номер 11.6 Мордкович — Подробные Ответы

Постройте прямую ах + by = с, если: а) а = —2, b = 3, с = 4; г) а = 4, b = 0, с = -6; б) а = 1, b = —5, с = 0; д) а = —3, b = 0, с = 0; в) а = 0, b = —1, с = —3; е) а = 0, b = 0,5, с = 0.

Общий вид линейного уравнения с двумя переменными:

\( ax + by = c \)

а) Если \( a = -2 \), \( b = 3 \), \( c = 4 \):
\( -2x + 3y = 4 \)

Если \( x = 0 \), то:
\( -2 \cdot 0 + 3y = 4 \)
\( 3y = 4 \)
\( y = \frac{4}{3} = 1\frac{1}{3} \Longrightarrow \left(0; 1\frac{1}{3}\right) \) — точка графика.

Если \( y = 0 \), то:
\( -2x + 3 \cdot 0 = 4 \)
\( -2x = 4 \)
\( x = -2 \Longrightarrow (-2; 0) \) — точка графика.

б) Если \( a = 1 \), \( b = -5 \), \( c = 0 \):
\( x — 5y = 0 \)

Если \( x = 0 \), то:
\( 0 — 5y = 0 \)
\( -5y = 0 \)
\( y = 0 \Longrightarrow (0; 0) \) — точка графика.

Если \( x = 5 \), то:
\( 5 — 5y = 0 \)
\( 5y = 5 \)
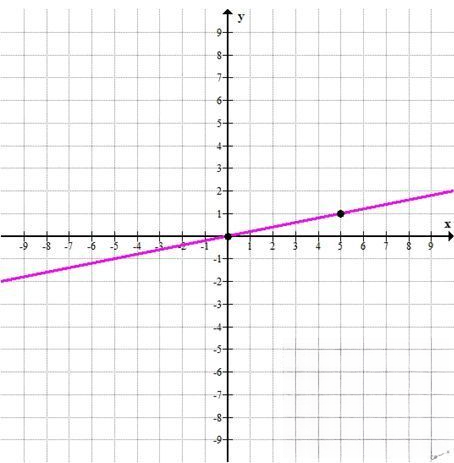
\( y = 1 \Longrightarrow (5; 1) \) — точка графика.

в) Если \( a = 0 \), \( b = -1 \), \( c = -3 \):
\( -y = -3 \Longrightarrow y = 3 \)

г) Если \( a = 4 \), \( b = 0 \), \( c = -6 \):
\( 4x = -6 \Longrightarrow x = \frac{-6}{4} = -1{,}5 \)

д) Если \( a = -3 \), \( b = 0 \), \( c = 0 \):
\( -3x = 0 \Longrightarrow x = 0 \)

е) Если \( a = 0 \), \( b = 0{,}5 \), \( c = 0 \):
\( 0{,}5y = 0 \Longrightarrow y = 0 \)

Общий вид линейного уравнения с двумя переменными:
\( ax + by = c \)

а) Дано: \( a = -2 \), \( b = 3 \), \( c = 4 \)
Подставим коэффициенты в уравнение:
\( -2x + 3y = 4 \)

Найдём точки пересечения графика с осями координат.

Если \( x = 0 \):
\( -2 \cdot 0 + 3y = 4 \)
\( 3y = 4 \)
\( y = \frac{4}{3} = 1\frac{1}{3} \)
Получаем точку: \( \left(0; 1\frac{1}{3}\right) \) — точка пересечения с осью \( Oy \).

Если \( y = 0 \):
\( -2x + 3 \cdot 0 = 4 \)
\( -2x = 4 \)
\( x = \frac{4}{-2} = -2 \)
Получаем точку: \( (-2; 0) \) — точка пересечения с осью \( Ox \).

График — прямая, проходящая через эти две точки.

б) Дано: \( a = 1 \), \( b = -5 \), \( c = 0 \)
Уравнение: \( x — 5y = 0 \)

Если \( x = 0 \):
\( 0 — 5y = 0 \)
\( -5y = 0 \)
\( y = 0 \)
Получаем точку: \( (0; 0) \) — начало координат.

Если \( x = 5 \):
\( 5 — 5y = 0 \)
\( 5y = 5 \)
\( y = 1 \)
Получаем точку: \( (5; 1) \)

График — прямая, проходящая через начало координат и точку \( (5; 1) \). Уравнение можно записать как \( y = \frac{1}{5}x \).

в) Дано: \( a = 0 \), \( b = -1 \), \( c = -3 \)
Уравнение: \( 0 \cdot x + (-1)y = -3 \) → \( -y = -3 \)
Решим:
\( y = 3 \)

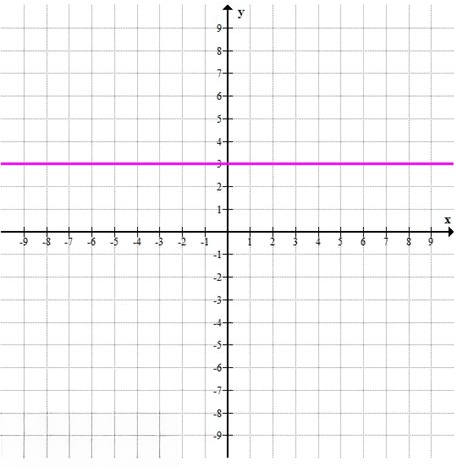
Это уравнение не содержит переменной \( x \), значит, график — горизонтальная прямая, параллельная оси \( Ox \), проходящая через \( y = 3 \).

Точка пересечения с осью \( Oy \): \( (0; 3) \)

г) Дано: \( a = 4 \), \( b = 0 \), \( c = -6 \)
Уравнение: \( 4x + 0 \cdot y = -6 \) → \( 4x = -6 \)
Решим:
\( x = \frac{-6}{4} = -1{,}5 \)

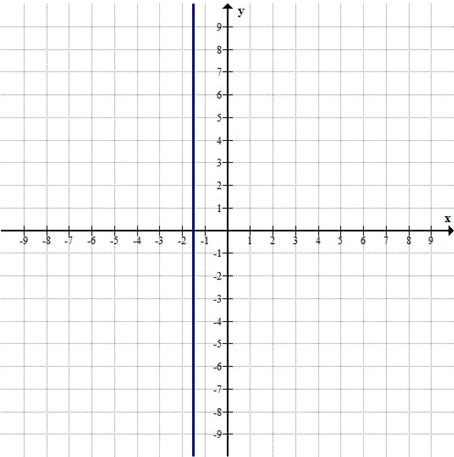
Это уравнение не содержит переменной \( y \), значит, график — вертикальная прямая, параллельная оси \( Oy \), проходящая через \( x = -1{,}5 \).

Точка пересечения с осью \( Ox \): \( (-1{,}5; 0) \)

д) Дано: \( a = -3 \), \( b = 0 \), \( c = 0 \)
Уравнение: \( -3x + 0 \cdot y = 0 \) → \( -3x = 0 \)
Решим:
\( x = 0 \)

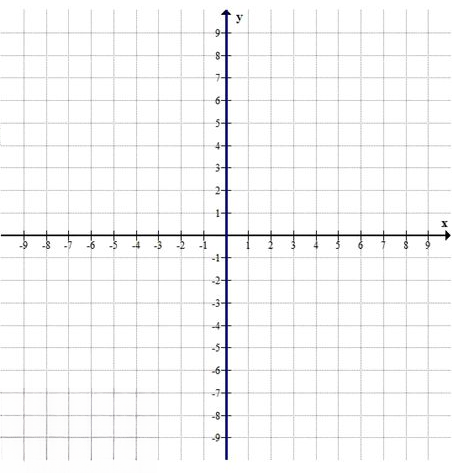
График — это сама ось ординат (\( Oy \)), так как \( x = 0 \) при любом \( y \).

е) Дано: \( a = 0 \), \( b = 0{,}5 \), \( c = 0 \)
Уравнение: \( 0 \cdot x + 0{,}5y = 0 \) → \( 0{,}5y = 0 \)
Решим:
\( y = 0 \)

График — это сама ось абсцисс (\( Ox \)), так как \( y = 0 \) при любом \( x \).

Вывод:
В каждом случае построен график линейного уравнения с двумя переменными. При нулевых коэффициентах при одной из переменных получаются вертикальные или горизонтальные прямые. Все решения выполнены по правилам алгебры.