Учебное пособие «Алгебра, 7 класс» авторства Мордковича, Мардахаева и Семенова является важным ресурсом для школьников, желающих расширить свои знания в алгебре. Книга выделяется содержательной насыщенностью и продуманной методической организацией, что способствует более легкому и интересному освоению математического материала.
ГДЗ по Алгебре 7 Класс Номер 12.10 Мордкович — Подробные Ответы
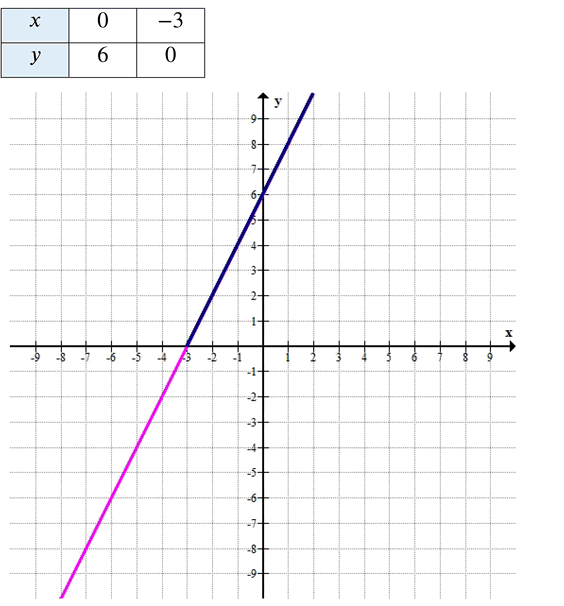
Постройте график линейной функции у = 2х + 6. а) Найдите координаты точки пересечения графика с осью Ох. б) Выделите ту часть графика, которая лежит выше оси абсцисс. Какие по знаку значения у соответствуют выделенной части графика? Какие значения принимает при этом выражение 2х + 6? в) Определите, какие значения х соответствуют выделенной в пункте «б» части графика. г) При каких значениях х выполняется неравенство у < 0?
\( y = 2x + 6 \)
а) \( (-3; 0) \) — точка пересечения с осью \( Ox \).
б) Часть, которая лежит выше оси абсцисс, выделена синим цветом.
Выделенной части графика соответствуют положительные значения \( y \) (\( y > 0 \)).
Выражение \( 2x + 6 \) так же принимает положительные значения.
в) Выделенной части графика соответствуют значения \( x \) больше \( -3 \) (\( x > -3 \)).
г) \( y < 0 \) при \( x < -3 \).
Дано уравнение: \( y = 2x + 6 \)
Это линейная функция, графиком которой является прямая с угловым коэффициентом \( 2 \) и свободным членом \( 6 \).
Найдём две точки для построения графика:
При \( x = 0 \): \( y = 2 \cdot 0 + 6 = 6 \) → точка \( (0; 6) \)
При \( x = -3 \): \( y = 2 \cdot (-3) + 6 = -6 + 6 = 0 \) → точка \( (-3; 0) \)
а) Точка пересечения с осью \( Ox \):
На оси абсцисс значение \( y = 0 \).
Решим уравнение: \( 2x + 6 = 0 \)
\( 2x = -6 \)
\( x = -3 \)
Следовательно, точка пересечения с осью \( Ox \) — \( (-3; 0) \)
б) Часть графика, расположенная выше оси \( Ox \), соответствует положительным значениям функции \( y > 0 \).
Выражение \( 2x + 6 \) принимает положительные значения, когда:
\( 2x + 6 > 0 \)
\( 2x > -6 \)
\( x > -3 \)
Значит, при \( x > -3 \) значения \( y \) положительны.
в) Выделенной части графика (выше оси \( Ox \)) соответствуют значения \( x \), большие \( -3 \), то есть \( x > -3 \).
Это следует из решения неравенства \( 2x + 6 > 0 \).
г) Значения \( y < 0 \) наблюдаются тогда, когда график находится ниже оси \( Ox \).
Решим неравенство: \( 2x + 6 < 0 \)
\( 2x < -6 \)
\( x < -3 \)
Следовательно, \( y < 0 \) при \( x < -3 \).