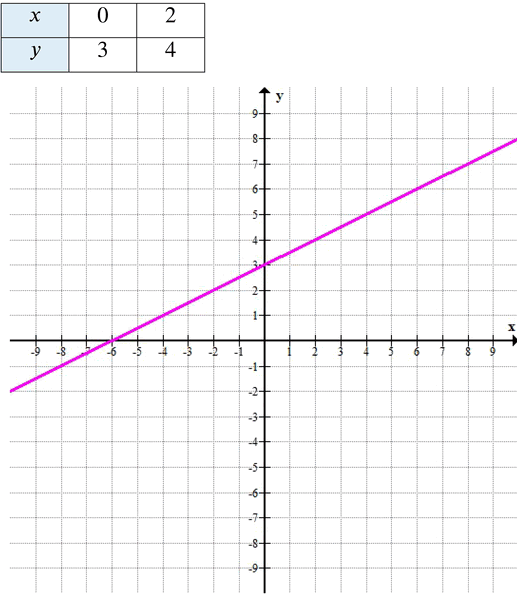ГДЗ по Алгебре 7 Класс Номер 12.14 Мордкович — Подробные Ответы

12.14. Постройте график линейной функции у = 0,5x + 3 и с его помощью найдите: а) координаты точки пересечения графика с осью абсцисс; б) все значения аргумента, при которых выполняется неравенство у < 0; в) решение неравенства 0,5x + 3 > 0; г) значения x, при которых выполняется неравенство у > 1.

\( y = 0{,}5x + 3 \)

а) \( (-6; 0) \) — точка пересечения с осью \( Ox \).

б) \( y < 0 \) при \( x < -6 \).

в) \( 0{,}5x + 3 > 0 \), то есть, \( y > 0 \) при \( x > -6 \).

г) \( y > 1 \) при \( x > -4 \).

Дано уравнение: \( y = 0{,}5x + 3 \)

Это линейная функция с угловым коэффициентом \( 0{,}5 \) и свободным членом \( 3 \).

Найдём две точки для построения графика:
При \( x = 0 \): \( y = 0{,}5 \cdot 0 + 3 = 3 \) → точка \( (0; 3) \)
При \( x = 2 \): \( y = 0{,}5 \cdot 2 + 3 = 1 + 3 = 4 \) → точка \( (2; 4) \)

а) Точка пересечения с осью \( Ox \) — это точка, где \( y = 0 \).
Решим уравнение:
\( 0{,}5x + 3 = 0 \)
\( 0{,}5x = -3 \)
\( x = -6 \)
Следовательно, точка пересечения с осью абсцисс: \( (-6; 0) \)

б) Найдём, при каких значениях \( x \) выполняется условие \( y < 0 \):
\( 0{,}5x + 3 < 0 \)
\( 0{,}5x < -3 \)
\( x < -6 \)
Значит, \( y < 0 \) при \( x < -6 \)

в) Рассмотрим неравенство \( y > 0 \):
\( 0{,}5x + 3 > 0 \)
\( 0{,}5x > -3 \)
\( x > -6 \)
Следовательно, выражение \( 0{,}5x + 3 \) принимает положительные значения при \( x > -6 \)

г) Найдём, при каких \( x \) выполняется условие \( y > 1 \):
\( 0{,}5x + 3 > 1 \)
\( 0{,}5x > -2 \)
\( x > -4 \)
Значит, \( y > 1 \) при \( x > -4 \)

Вывод:
График функции \( y = 0{,}5x + 3 \) пересекает ось \( Ox \) в точке \( (-6; 0) \).
— При \( x < -6 \) — значения функции отрицательны (\( y < 0 \)).
— При \( x > -6 \) — значения функции положительны (\( y > 0 \)).
— При \( x > -4 \) — значения функции больше единицы (\( y > 1 \)).