ГДЗ по Алгебре 7 Класс Номер 12.16 Мордкович — Подробные Ответы

С помощью графика линейной функции решите неравенство:

а) 0,5x — 2 > 0;

б) \( -x + 5 \geq 0 \);

в) \(\frac{1}{3}\) х — 1 < 0;

г) y =\( 3 — 2x \leq 0 \).

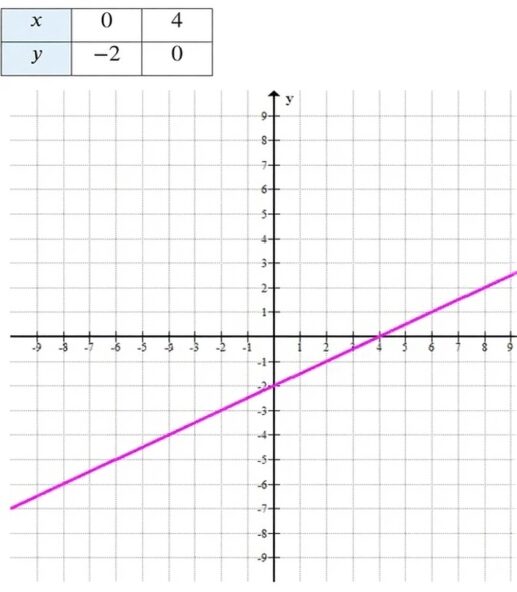
а) \( y = 0{,}5x — 2 \)

\( 0{,}5x — 2 > 0 \) при \( x > 4 \).

Ответ: при \( x > 4 \).

б) \( y = -x + 5 \)

\( -x + 5 \geq 0 \) при \( x \leq 5 \).

Ответ: при \( x \leq 5 \).

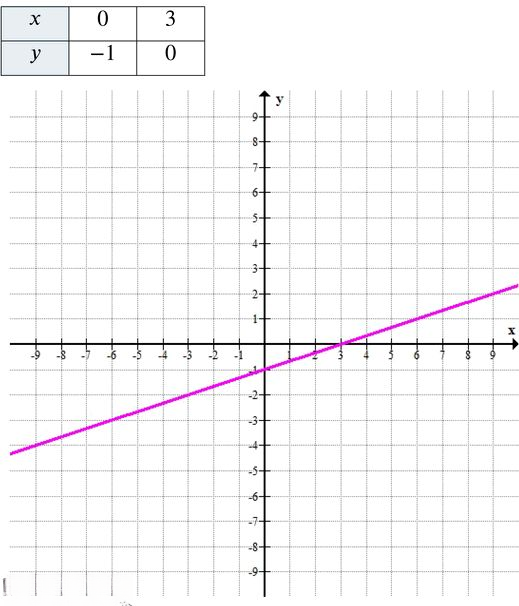
в) \( y = \frac{1}{3}x — 1 \)

\( \frac{1}{3}x — 1 < 0 \) при \( x < 3 \).

Ответ: при \( x < 3 \).

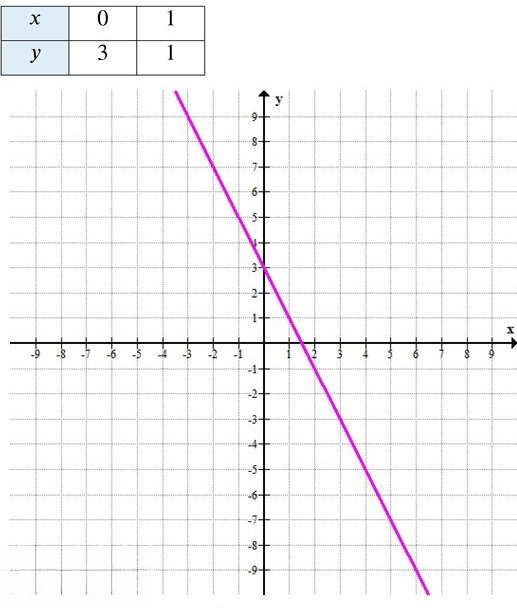
г) \( y = 3 — 2x \)

\( 3 — 2x \leq 0 \) при \( x \geq 1{,}5 \).

Ответ: при \( x \geq 1{,}5 \).

а) Уравнение: \( y = 0{,}5x — 2 \)

Это линейная функция с угловым коэффициентом \( 0{,}5 \) и свободным членом \( -2 \).

Найдём точки пересечения графика с осями:

— При \( x = 0 \):
\( y = 0{,}5 \cdot 0 — 2 = -2 \) → точка \( (0; -2) \)

— При \( y = 0 \):
\( 0 = 0{,}5x — 2 \)
\( 0{,}5x = 2 \)
\( x = 4 \) → точка \( (4; 0) \)

Таблица значений:

Решим неравенство \( 0{,}5x — 2 > 0 \):

Приравняем выражение к нулю:
\( 0{,}5x — 2 = 0 \)
\( 0{,}5x = 2 \)
\( x = 4 \)

Функция возрастает (угловой коэффициент положителен), значит, значения функции больше нуля при \( x > 4 \).

Ответ: \( x > 4 \)

б) Уравнение: \( y = -x + 5 \)

Линейная функция с угловым коэффициентом \( -1 \) и свободным членом \( 5 \).

Найдём точки пересечения:

— При \( x = 0 \):
\( y = -0 + 5 = 5 \) → точка \( (0; 5) \)

— При \( y = 0 \):
\( 0 = -x + 5 \)
\( x = 5 \) → точка \( (5; 0) \)

Таблица значений:

Решим неравенство \( -x + 5 \geq 0 \):

Приравняем к нулю:
\( -x + 5 = 0 \)
\( x = 5 \)

Функция убывает (угловой коэффициент отрицателен), значит, значения функции неотрицательны при \( x \leq 5 \).

Ответ: \( x \leq 5 \)

в) Уравнение: \( y = \frac{1}{3}x — 1 \)

Линейная функция с угловым коэффициентом \( \frac{1}{3} \) и свободным членом \( -1 \).

Найдём точки пересечения:

— При \( x = 0 \):
\( y = \frac{1}{3} \cdot 0 — 1 = -1 \) → точка \( (0; -1) \)

— При \( y = 0 \):
\( 0 = \frac{1}{3}x — 1 \)
\( \frac{1}{3}x = 1 \)
\( x = 3 \) → точка \( (3; 0) \)

Таблица значений:

Решим неравенство \( \frac{1}{3}x — 1 < 0 \):

Приравняем к нулю:
\( \frac{1}{3}x — 1 = 0 \)
\( \frac{1}{3}x = 1 \)
\( x = 3 \)

Функция возрастает, значит, значения функции меньше нуля при \( x < 3 \).

Ответ: \( x < 3 \)

г) Уравнение: \( y = 3 — 2x \)

Линейная функция с угловым коэффициентом \( -2 \) и свободным членом \( 3 \).

Найдём точки пересечения:

— При \( x = 0 \):
\( y = 3 — 2 \cdot 0 = 3 \) → точка \( (0; 3) \)

— При \( y = 0 \):
\( 0 = 3 — 2x \)
\( 2x = 3 \)
\( x = 1{,}5 \) → точка \( (1{,}5; 0) \)

Решим неравенство \( 3 — 2x \leq 0 \):

Приравняем к нулю:
\( 3 — 2x = 0 \)
\( -2x = -3 \)
\( x = 1{,}5 \)

Функция убывает, значит, значения функции меньше или равны нулю при \( x \geq 1{,}5 \).

Ответ: \( x \geq 1{,}5 \)

Итоговые ответы:

а) \( x > 4 \)
б) \( x \leq 5 \)
в) \( x < 3 \)
г) \( x \geq 1{,}5 \)