ГДЗ по Алгебре 7 Класс Номер 12.18 Мордкович — Подробные Ответы

Как расположен в координатной плоскости хОу график линейной функции у = kx + m, если известно, что:

а) k > 0, m = 0;
б) k < 0, m = 0;
в) k = 0, \( m \neq 0 \);
г) k = 0, m = 0.

\( y = kx + m \)

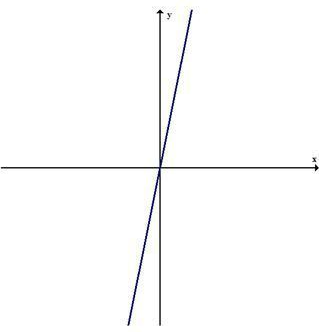
а) Если \( k > 0 \), \( m = 0 \), то:

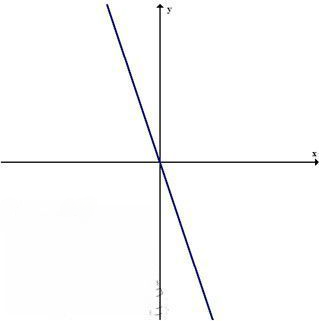
б) Если \( k < 0 \), \( m = 0 \), то:

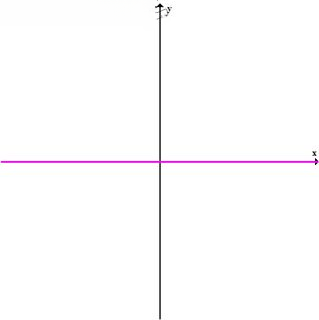
в) Если \( k = 0 \), \( m \neq 0 \), то:

г) Если \( k = 0 \), \( m = 0 \), то:

Общий вид линейной функции:
\( y = kx + m \)

Здесь:
— \( k \) — угловой коэффициент (определяет наклон прямой),
— \( m \) — свободный член (определяет сдвиг по оси \( Oy \)).

Рассмотрим частные случаи:

а) Если \( k > 0 \), \( m = 0 \), то:

Уравнение принимает вид:
\( y = kx \), где \( k > 0 \)

Это прямая, проходящая через начало координат, и имеющая положительный наклон (возрастающая функция).
График расположен в первой и третьей четвертях.

Пример: \( y = 2x \)

б) Если \( k < 0 \), \( m = 0 \), то:

Уравнение:
\( y = kx \), где \( k < 0 \)

Это прямая, проходящая через начало координат, но с отрицательным наклоном (убывающая функция).
График расположен во второй и четвёртой четвертях.

Пример: \( y = -3x \)

в) Если \( k = 0 \), \( m \neq 0 \), то:

Уравнение:
\( y = 0 \cdot x + m = m \), где \( m \neq 0 \)

Это горизонтальная прямая, параллельная оси \( Ox \), проходящая через точку \( (0; m) \).

Примеры:
— \( y = 4 \) — прямая выше оси \( Ox \)
— \( y = -2 \) — прямая ниже оси \( Ox \)

г) Если \( k = 0 \), \( m = 0 \), то:

Уравнение:
\( y = 0 \cdot x + 0 = 0 \)

Это ось абсцисс — горизонтальная прямая, совпадающая с осью \( Ox \).

Вывод:
В зависимости от значений коэффициентов \( k \) и \( m \), график линейной функции может быть:
— возрастающей прямой,
— убывающей прямой,
— горизонтальной прямой,
— или самой осью \( Ox \).

Каждый случай имеет свою геометрическую интерпретацию на координатной плоскости.