ГДЗ по Алгебре 7 Класс Номер 12.6 Мордкович — Подробные Ответы

Постройте график линейной функции: а) у = х — 4; г) у = 6 — х; б) у = -2х + 1; д) у = 3х + 2; в) у = \(\frac{1}{3}\) х — 3; е) y = -0,5x + 4.

а) \( y = x — 4 \);

б) \( y = -2x + 1 \);

в) \( y = \frac{1}{3}x — 3 \);

г) \( y = 6 — x \);

д) \( y = 3x + 2 \);

е) \( y = -0{,}5x + 4 \);

а) \( y = x — 4 \)

Это линейная функция с угловым коэффициентом \( k = 1 > 0 \), значит, функция возрастает.

Найдём значения:
— При \( x = 0 \):
\( y = 0 — 4 = -4 \) → точка \( (0; -4) \)
— При \( x = 4 \):
\( y = 4 — 4 = 0 \) → точка \( (4; 0) \)

Таблица значений:

График — прямая, проходящая через точки \( (0; -4) \) и \( (4; 0) \).
Пересекает ось \( Oy \) в точке \( (0; -4) \), ось \( Ox \) — в точке \( (4; 0) \).

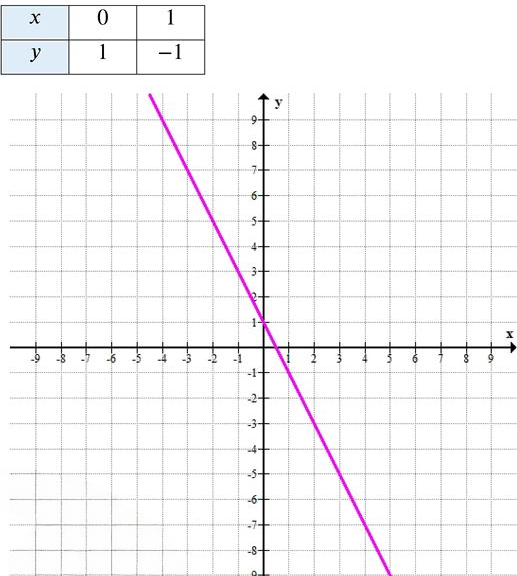
б) \( y = -2x + 1 \)

Угловой коэффициент \( k = -2 < 0 \) → функция убывает.

Значения:
— При \( x = 0 \):
\( y = -2 \cdot 0 + 1 = 1 \) → точка \( (0; 1) \)
— При \( x = 1 \):
\( y = -2 \cdot 1 + 1 = -2 + 1 = -1 \) → точка \( (1; -1) \)

Таблица значений:

График — прямая, идущая сверху слева направо вниз.
Проходит через точку пересечения с осью \( Oy \) — \( (0; 1) \).

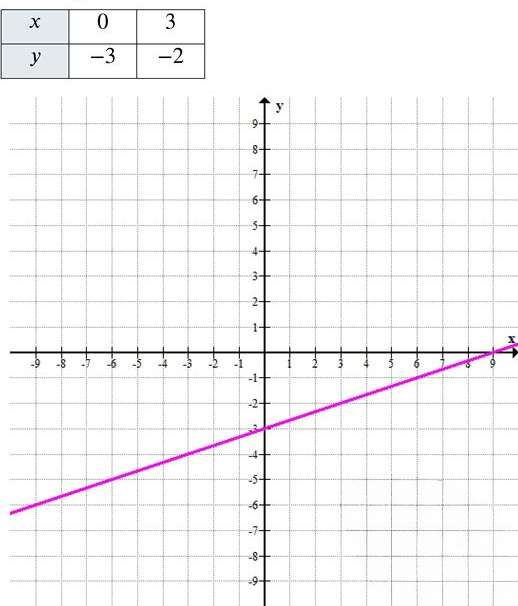
в) \( y = \frac{1}{3}x — 3 \)

Коэффициент \( k = \frac{1}{3} > 0 \) → функция возрастает, но медленно.

Вычисления:
— При \( x = 0 \):
\( y = \frac{1}{3} \cdot 0 — 3 = -3 \) → точка \( (0; -3) \)
— При \( x = 3 \):
\( y = \frac{1}{3} \cdot 3 — 3 = 1 — 3 = -2 \) → точка \( (3; -2) \)

Таблица значений:

Прямая слабо наклонена к оси абсцисс. Пересекает ось \( Oy \) в точке \( (0; -3) \).

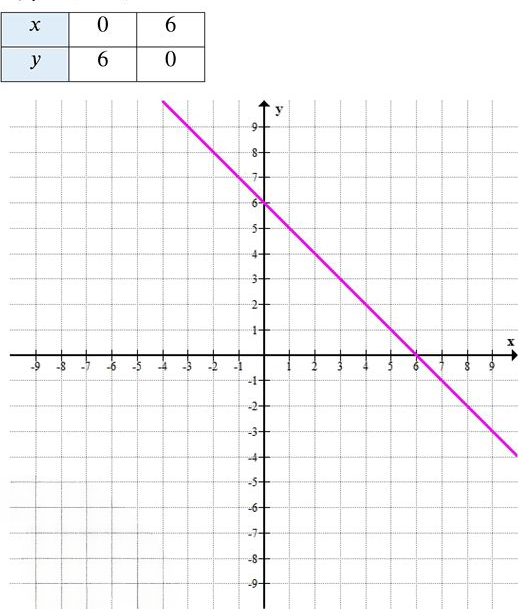
г) \( y = 6 — x \)

Можно записать как \( y = -x + 6 \), где \( k = -1 < 0 \) → функция убывает.

Значения:
— При \( x = 0 \):
\( y = 6 — 0 = 6 \) → точка \( (0; 6) \)
— При \( x = 6 \):
\( y = 6 — 6 = 0 \) → точка \( (6; 0) \)

Таблица значений:

График — убывающая прямая, проходящая через \( (0; 6) \) и \( (6; 0) \), расположенная в первой четверти и пересекающая обе оси.

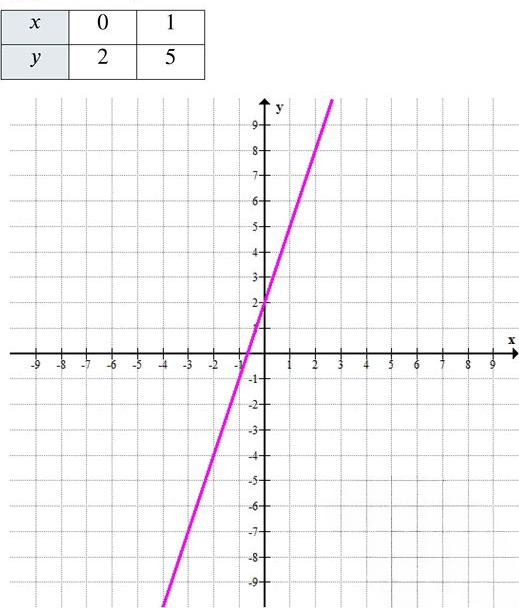
д) \( y = 3x + 2 \)

Коэффициент \( k = 3 > 0 \) → функция возрастает быстро.

Значения:
— При \( x = 0 \):
\( y = 3 \cdot 0 + 2 = 2 \) → точка \( (0; 2) \)
— При \( x = 1 \):
\( y = 3 \cdot 1 + 2 = 5 \) → точка \( (1; 5) \)

Таблица значений:

Прямая имеет крутой положительный наклон. Проходит через \( (0; 2) \) — точку на оси ординат.

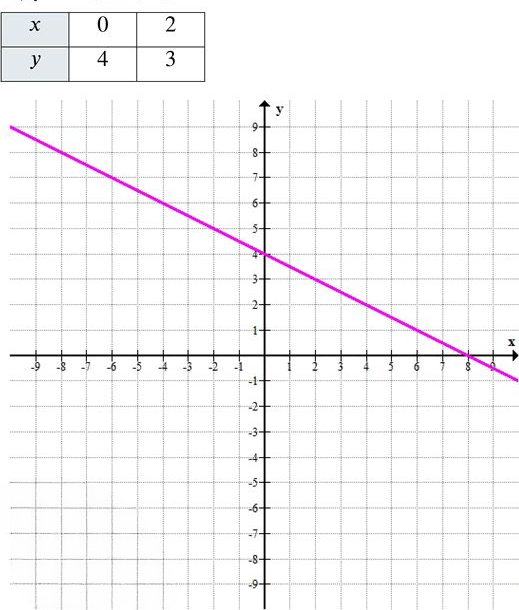
е) \( y = -0{,}5x + 4 \)

Угловой коэффициент \( k = -0{,}5 < 0 \) → функция убывает, но медленно.

Вычисления:
— При \( x = 0 \):
\( y = -0{,}5 \cdot 0 + 4 = 4 \) → точка \( (0; 4) \)
— При \( x = 2 \):
\( y = -0{,}5 \cdot 2 + 4 = -1 + 4 = 3 \) → точка \( (2; 3) \)

Таблица значений:

График — пологая убывающая прямая, начинающаяся в \( (0; 4) \) и плавно опускающаяся вправо.

Вывод:
Для каждой из шести линейных функций построены таблицы значений по двум точкам, что достаточно для построения графика — прямой линии.
Направление наклона определяется знаком углового коэффициента:
— \( k > 0 \) — возрастание,
— \( k < 0 \) — убывание.