ГДЗ по Алгебре 7 Класс Номер 12.7 Мордкович — Подробные Ответы

Постройте график линейной функции в соответствующей системе координат:

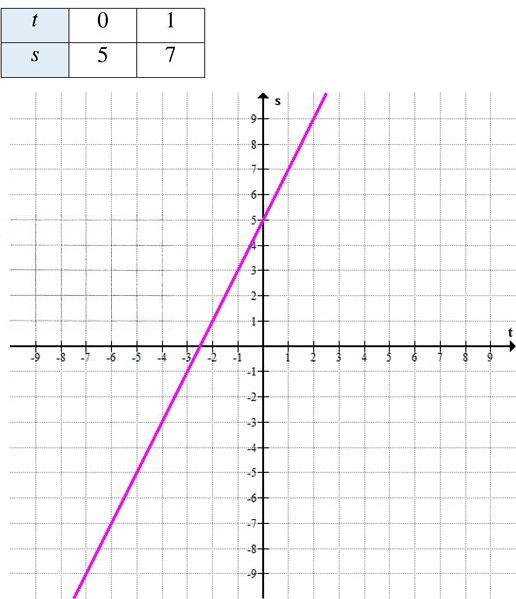
а) \( s = 2t + 5 \)

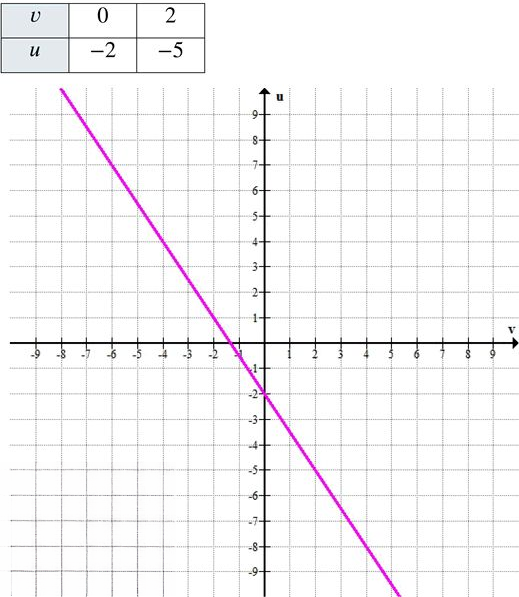
б) \( u = -\frac{3}{2}v — 2 \)

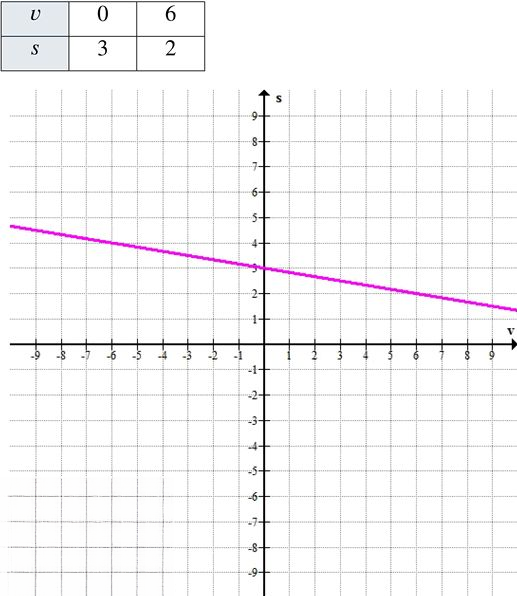
в) \( s = -\frac{v}{6} + 3 \)

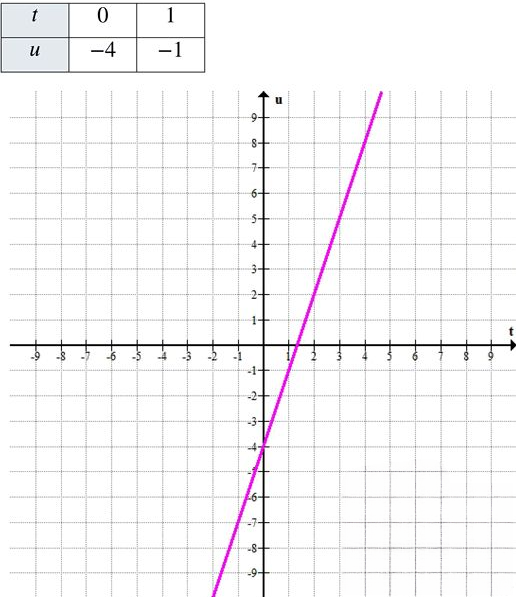
г) \( u = 3t — 4 \)

а)
\( s = 2t + 5 \)

б)
\( u = -1.5v — 2 \)

в)
\( s = -\frac{v}{6} + 3 \)

г)
\( u = 3t — 4 \)

а) Уравнение: \( s = 2t + 5 \)

Это линейная функция, в которой переменная \( s \) зависит от переменной \( t \).
Найдём значения \( s \) при заданных значениях \( t \).

— При \( t = 0 \):
\( s = 2 \cdot 0 + 5 = 0 + 5 = 5 \)

— При \( t = 1 \):
\( s = 2 \cdot 1 + 5 = 2 + 5 = 7 \)

Результаты занесены в таблицу:

б) Уравнение: \( u = -1{,}5v — 2 \)

Это линейная функция с отрицательным угловым коэффициентом.
Найдём значения \( u \) при заданных значениях \( v \).

— При \( v = 0 \):
\( u = -1{,}5 \cdot 0 — 2 = 0 — 2 = -2 \)

— При \( v = 2 \):
\( u = -1{,}5 \cdot 2 — 2 = -3 — 2 = -5 \)

Результаты занесены в таблицу:

в) Уравнение: \( s = -\frac{v}{6} + 3 \)

Это линейная функция с отрицательным наклоном и свободным членом 3.
Найдём значения \( s \) при заданных значениях \( v \).

— При \( v = 0 \):
\( s = -\frac{0}{6} + 3 = 0 + 3 = 3 \)

— При \( v = 6 \):
\( s = -\frac{6}{6} + 3 = -1 + 3 = 2 \)

Результаты занесены в таблицу:

г) Уравнение: \( u = 3t — 4 \)

Это линейная функция с положительным угловым коэффициентом.
Найдём значения \( u \) при заданных значениях \( t \).

— При \( t = 0 \):
\( u = 3 \cdot 0 — 4 = 0 — 4 = -4 \)

— При \( t = 1 \):
\( u = 3 \cdot 1 — 4 = 3 — 4 = -1 \)

Вывод:
Во всех четырёх случаях выполнена подстановка значений независимой переменной в линейное уравнение и вычислено соответствующее значение зависимой переменной. Полученные пары значений можно использовать для построения графиков прямых.