ГДЗ по Алгебре 7 Класс Номер 13.1 Мордкович — Подробные Ответы

Постройте график линейной функции в соответствующей системе координат:

а) у = — x;  д) у = -3x;
б) у = \(\frac{1}{3}\) x;
в) у = 0,5x;
г) s = t;
д) у = -3x;
е) s = 2t.

а)
\( y = -x \)

б)
\( y = \frac{1}{3}x \)

в)
\( y = 0.5x \)

г)
\( s = t \)

д)
\( y = -3x \)

е)
\( s = 2t \)

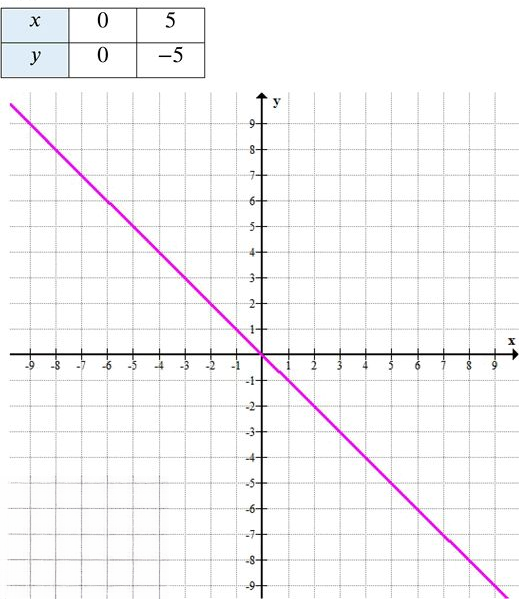
а) Уравнение: \( y = -x \)

Это линейная функция, проходящая через начало координат с угловым коэффициентом \( -1 \). График — прямая, расположенная во второй и четвёртой четвертях.

Найдём две точки для построения:

— При \( x = 0 \):
\( y = -0 = 0 \) → точка \( (0; 0) \)

— При \( x = 5 \):
\( y = -5 \) → точка \( (5; -5) \)

Таблица значений:

График симметричен относительно начала координат.

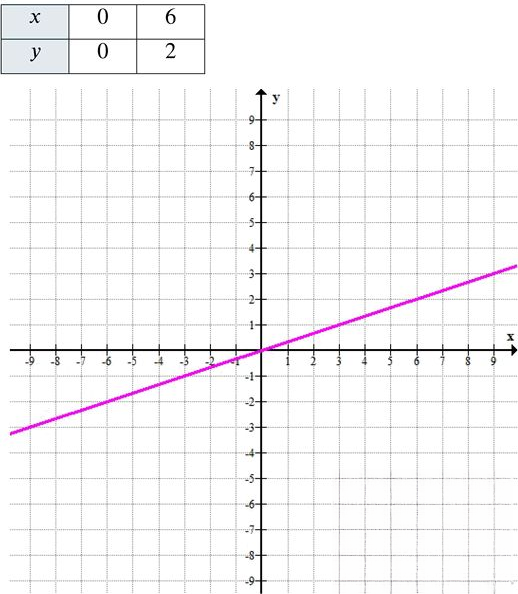
б) Уравнение: \( y = \frac{1}{3}x \)

Линейная функция с положительным угловым коэффициентом \( \frac{1}{3} \), проходит через начало координат. График расположен в первой и третьей четвертях.

Найдём точки:

— При \( x = 0 \):
\( y = \frac{1}{3} \cdot 0 = 0 \) → точка \( (0; 0) \)

— При \( x = 6 \):
\( y = \frac{1}{3} \cdot 6 = 2 \) → точка \( (6; 2) \)

Таблица значений:

Прямая имеет малый наклон — медленно возрастает.

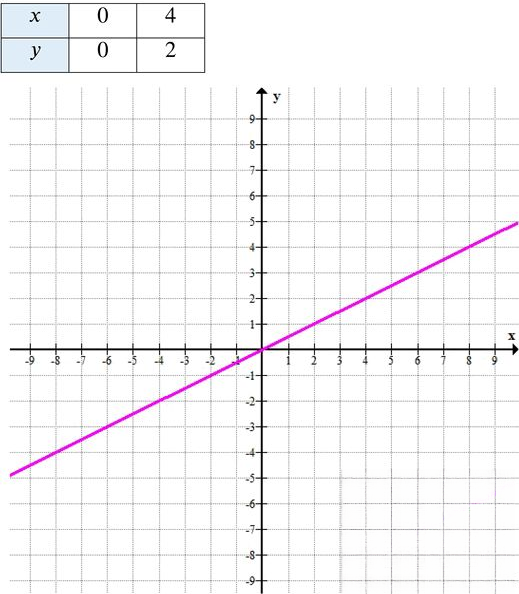
в) Уравнение: \( y = 0{,}5x \)

Линейная функция с угловым коэффициентом \( 0{,}5 \), проходит через начало координат. График — возрастающая прямая в первой и третьей четвертях.

Найдём точки:

— При \( x = 0 \):
\( y = 0{,}5 \cdot 0 = 0 \) → точка \( (0; 0) \)

— При \( x = 4 \):
\( y = 0{,}5 \cdot 4 = 2 \) → точка \( (4; 2) \)

Таблица значений:

Функция возрастает медленнее, чем при \( k = 1 \).

г) Уравнение: \( s = t \)

Функция задана переменными \( s \) и \( t \), но это та же прямая пропорциональность. График — биссектриса первого и третьего координатных углов.

Найдём точки:

— При \( t = 0 \):
\( s = 0 \) → точка \( (0; 0) \)

— При \( t = 4 \):
\( s = 4 \) → точка \( (4; 4) \)

Таблица значений:

График — прямая под углом 45° к осям.

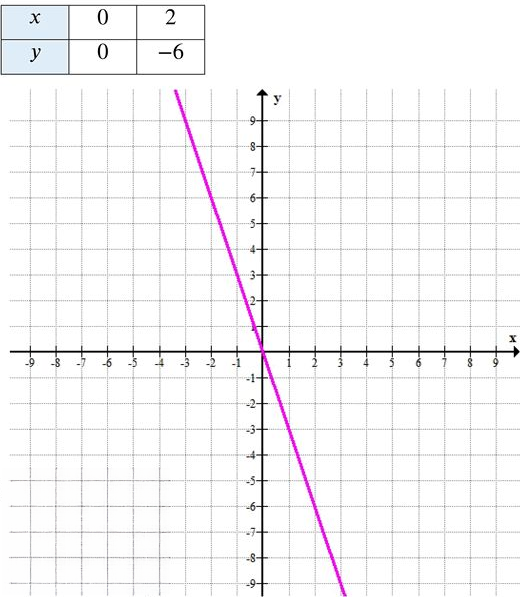
д) Уравнение: \( y = -3x \)

Линейная функция с отрицательным угловым коэффициентом \( -3 \), проходит через начало координат. График — убывающая прямая, расположенная во второй и четвёртой четвертях, с крутым наклоном.

Найдём точки:

— При \( x = 0 \):
\( y = -3 \cdot 0 = 0 \) → точка \( (0; 0) \)

— При \( x = 2 \):
\( y = -3 \cdot 2 = -6 \) → точка \( (2; -6) \)

Функция быстро убывает.

е) Уравнение: \( s = 2t \)

Это линейная функция, заданная переменными \( s \) и \( t \). График — прямая, проходящая через начало координат, с угловым коэффициентом \( 2 \).
Функция возрастающая, так как коэффициент положительный.
График расположен в первой и третьей четвертях.

Найдём две точки для построения графика:

— При \( t = 0 \):
\( s = 2 \cdot 0 = 0 \) → точка \( (0; 0) \)

— При \( t = 2 \):
\( s = 2 \cdot 2 = 4 \) → точка \( (2; 4) \)

Таблица значений:

Проведём прямую через точки \( (0; 0) \) и \( (2; 4) \).
Прямая имеет положительный наклон — при увеличении \( t \) на 1, значение \( s \) увеличивается на 2.

Вывод:
Все рассмотренные функции имеют вид \( y = kx \) — это прямые пропорциональности, графики которых проходят через начало координат.
Знак и величина коэффициента \( k \) определяют угол наклона и направление прямой.