ГДЗ по Алгебре 7 Класс Номер 13.7 Мордкович — Подробные Ответы

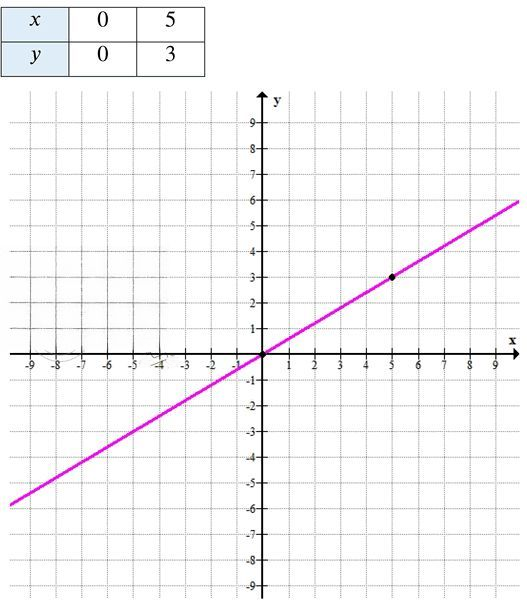
Постройте график линейной функции у = 0,6x. Найдите по графику:

а) решения неравенства 0,6x > О;

б) решения неравенства \( -3 \leq 0{,}6x \leq 0 \)

\( y = 0{,}6x \)

а) \( 0{,}6x > 0 \), то есть, \( y > 0 \) при \( x > 0 \).

б) \( -3 \leq 0{,}6x \leq 0 \), то есть, \( -3 \leq y \leq 0 \) при \( -5 \leq x \leq 0 \).

Дана функция:
\( y = 0{,}6x \)

Это линейная функция, графиком которой является прямая, проходящая через начало координат (так как свободный член отсутствует). Угловой коэффициент \( k = 0{,}6 > 0 \), значит, функция возрастает на всей области определения.

Таблица значений:

Найдём две точки для построения графика:

— При \( x = 0 \):
\( y = 0{,}6 \cdot 0 = 0 \) → точка \( (0; 0) \)

— При \( x = 5 \):
\( y = 0{,}6 \cdot 5 = 3 \) → точка \( (5; 3) \)

Таблица:

Прямая проходит через эти две точки и расположена в первой и третьей четвертях.

а) Определение, при каких \( x \) выполняется неравенство \( y > 0 \)

Рассмотрим неравенство:
\( 0{,}6x > 0 \)

Разделим обе части на \( 0{,}6 \) (положительное число, знак неравенства не меняется):
\( x > 0 \)

Так как функция возрастает и проходит через начало координат, она принимает положительные значения при всех \( x > 0 \).

Следовательно, \( y > 0 \) при \( x > 0 \).

б) Решение двойного неравенства: \( -3 \leq 0{,}6x \leq 0 \)

Перепишем в виде:
\( -3 \leq y \leq 0 \)

Найдём соответствующие значения \( x \):

1. Нижняя граница: \( 0{,}6x = -3 \)
\( x = \frac{-3}{0{,}6} = \frac{-30}{6} = -5 \)

2. Верхняя граница: \( 0{,}6x = 0 \)
\( x = 0 \)

Поскольку функция возрастает, все значения \( y \) из отрезка \([-3; 0]\) соответствуют значениям \( x \) от \(-5\) до \(0\).

Следовательно,
\( -3 \leq y \leq 0 \) при \( -5 \leq x \leq 0 \)

Вывод:
— Функция \( y = 0{,}6x \) возрастает.
— \( y > 0 \) при \( x > 0 \)
— \( y \in [-3; 0] \) при \( x \in [-5; 0] \)