Учебное пособие «Алгебра, 7 класс» авторства Мордковича, Мардахаева и Семенова является важным ресурсом для школьников, желающих расширить свои знания в алгебре. Книга выделяется содержательной насыщенностью и продуманной методической организацией, что способствует более легкому и интересному освоению математического материала.
ГДЗ по Алгебре 7 Класс Номер 13.9 Мордкович — Подробные Ответы
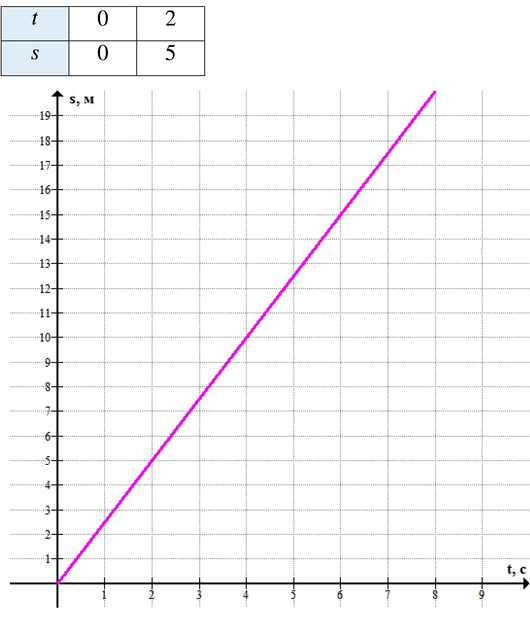
График движения материальной точки задан формулой s = 2,5t, где t — время в секундах, s — путь в метрах. Постройте график в системе координат sOt. С помощью графика найдите: а) путь, пройденный точкой за 2 с; б) время, за которое точка преодолеет 10 м; в) скорость движения точки.
\( s = 2{,}5t \), \( t \geq 0 \) и \( s \geq 0 \);
а) За 2 с точка пройдёт 5 м.
б) 10 м точка преодолеет за 4 с.
в) Скорость движения точки:
\( 10 : 4 = 2{,}5 \) (м/с).
Дана функция:
\( s = 2{,}5t \), где \( s \) — путь (в метрах), \( t \) — время (в секундах).
Условия: \( t \geq 0 \), \( s \geq 0 \) — движение начинается с начального момента времени и не может быть отрицательным.
Это уравнение прямой пропорциональности, описывающей равномерное прямолинейное движение. Коэффициент \( 2{,}5 \) — это скорость точки, выраженная в м/с.
Таблица значений:
Найдём две точки для построения графика:
— При \( t = 0 \):
\( s = 2{,}5 \cdot 0 = 0 \) → точка \( (0; 0) \)
— При \( t = 2 \):
\( s = 2{,}5 \cdot 2 = 5 \) → точка \( (2; 5) \)
Таблица:
График — луч, выходящий из начала координат в первой четверти, так как время и путь неотрицательны.
а) Сколько метров пройдёт точка за 2 секунды?
Подставим \( t = 2 \) в формулу:
\( s = 2{,}5 \cdot 2 = 5 \) (м)
Ответ: за 2 секунды точка пройдёт 5 метров.
б) За какое время точка преодолеет 10 метров?
Подставим \( s = 10 \) в уравнение:
\( 10 = 2{,}5t \)
Решим уравнение:
\( t = \frac{10}{2{,}5} = \frac{100}{25} = 4 \) (с)
Ответ: точка преодолеет 10 метров за 4 секунды.
в) Найти скорость движения точки
Скорость при равномерном движении определяется как отношение пройденного пути ко времени:
\( v = \frac{s}{t} \)
Из уравнения \( s = 2{,}5t \) следует, что коэффициент \( 2{,}5 \) и есть скорость.
Можно проверить на конкретных значениях:
\( v = \frac{10\ \text{м}}{4\ \text{с}} = 2{,}5\ \text{м/с} \)
Ответ: скорость движения точки составляет 2,5 м/с.
Вывод:
Функция \( s = 2{,}5t \) описывает равномерное движение точки со скоростью 2,5 м/с.
За каждую секунду точка проходит 2,5 метра.
Графически это представлено прямой линией, наклон которой соответствует скорости движения.