Учебное пособие «Алгебра, 7 класс» авторства Мордковича, Мардахаева и Семенова является важным ресурсом для школьников, желающих расширить свои знания в алгебре. Книга выделяется содержательной насыщенностью и продуманной методической организацией, что способствует более легкому и интересному освоению математического материала.
ГДЗ по Алгебре 7 Класс Номер 14.1 Мордкович — Подробные Ответы
Постройте график данной линейной функции и выделите его часть на заданном промежутке:
а) \( y = 3x \), \( x \in [-2; 0] \);
б) , ;
в) , ;
г) , ;
д) , ;
е) , ;
а) \( y = 3x \), \( x \in [-2; 0] \);
б) , ;
в) , ;
г) , ;
д) , ;
е) , ;
а) \( y = 3x \), \( x \in [-2; 0] \)
Найдём значения функции на концах промежутка:
При \( x = -2 \): \( y = 3 \cdot (-2) = -6 \) → точка \( (-2; -6) \)
При \( x = 0 \): \( y = 3 \cdot 0 = 0 \) → точка \( (0; 0) \)
Таблица значений:
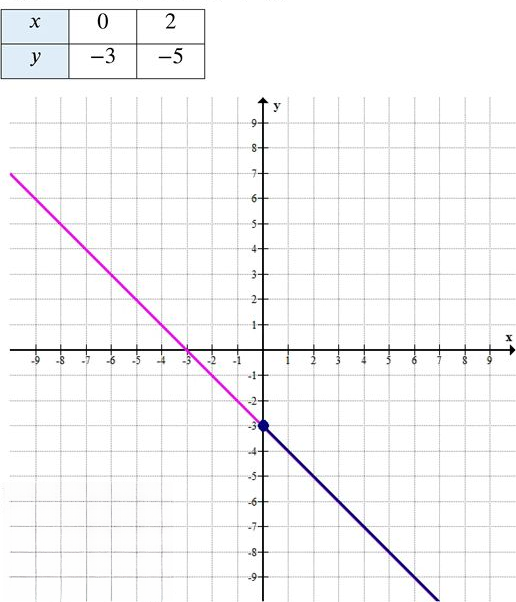
б) \( y = -x — 3 \), область определения: \( x \in [0; +\infty) \)
Функция линейная, убывающая (угловой коэффициент \( k = -1 < 0 \)).
График — луч, начинающийся в точке \( (0; -3) \) и уходящий вниз направо при увеличении \( x \).
Найдём две точки для построения графика:
— При \( x = 0 \):
\( y = -0 — 3 = -3 \) → точка \( (0; -3) \)
— При \( x = 2 \):
\( y = -2 — 3 = -5 \) → точка \( (2; -5) \)
Таблица значений:
Функция возрастает. График — отрезок, соединяющий точки \( (-2; -6) \) и \( (0; 0) \). Обе границы включены.
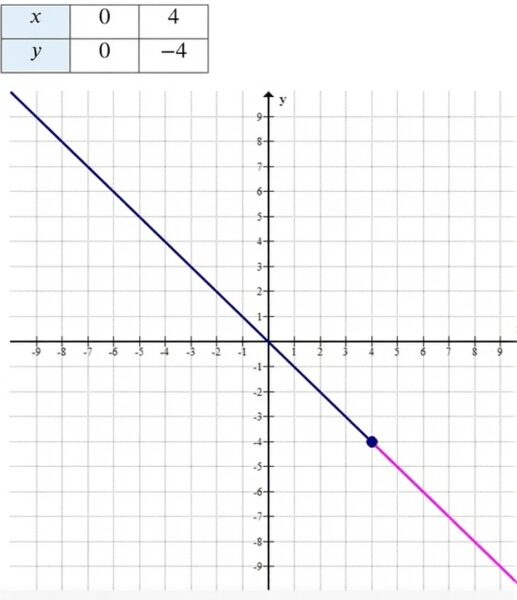
в) \( y = -2x + 4 \), \( x \in (-0{,}5; 4] \)
Найдём значения:
При \( x = 0 \): \( y = -2 \cdot 0 + 4 = 4 \) → точка \( (0; 4) \)
При \( x = 2 \): \( y = -2 \cdot 2 + 4 = 0 \) → точка \( (2; 0) \)
Таблица значений:
г) \( y = -x \), \( x \in (-\infty; 4] \)
Найдём значения:
При \( x = 0 \): \( y = -0 = 0 \) → точка \( (0; 0) \)
При \( x = 4 \): \( y = -4 \) → точка \( (4; -4) \)
Таблица значений:
График — луч, начинающийся в точке \( (4; -4) \) и уходящий в бесконечность при уменьшении \( x \). Конец при \( x = 4 \) — закрашен.
Область определения: \( x > -0{,}5 \) и \( x \leq 4 \).
Левый конец не включён (выколотая точка при \( x = -0{,}5 \)), правый — закрашен.
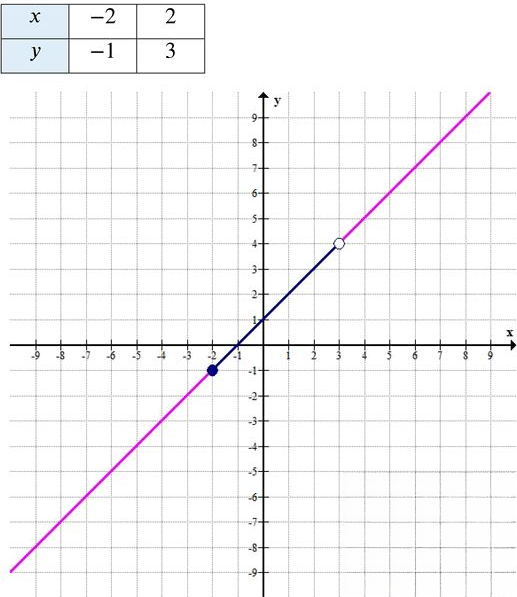
д) \( y = x + 1 \), \( x \in [-2; 3) \)
Найдём значения:
При \( x = -2 \): \( y = -2 + 1 = -1 \) → точка \( (-2; -1) \)
При \( x = 2 \): \( y = 2 + 1 = 3 \) → точка \( (2; 3) \)
Таблица значений:
Промежуток: \( -2 \leq x < 3 \).
Левый конец включён, правый — выколот.
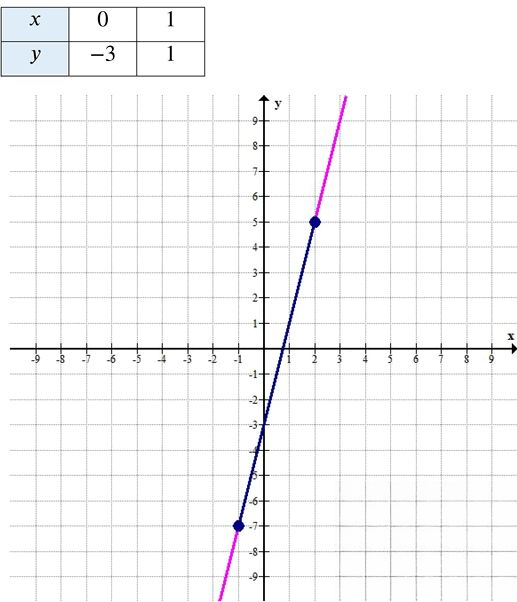
е) \( y = 4x — 3 \), \( x \in [-1; 2] \)
Найдём значения:
При \( x = 0 \): \( y = 4 \cdot 0 — 3 = -3 \) → точка \( (0; -3) \)
При \( x = 1 \): \( y = 4 \cdot 1 — 3 = 1 \) → точка \( (1; 1) \)
Таблица значений:
Функция возрастает. График — отрезок между точками \( (0; -3) \) и \( (1; 1) \), с концами при \( x = -1 \) и \( x = 2 \). Обе границы включены.