Учебное пособие «Алгебра, 7 класс» авторства Мордковича, Мардахаева и Семенова является важным ресурсом для школьников, желающих расширить свои знания в алгебре. Книга выделяется содержательной насыщенностью и продуманной методической организацией, что способствует более легкому и интересному освоению математического материала.
ГДЗ по Алгебре 7 Класс Номер 14.3 Мордкович — Подробные Ответы
Найдите наименьшее и наибольшее значения линейной функции: а) у = 2х на отрезке [—1; 2]; б) y = -x — 6 на полуинтервале [-10; 2); в) y = \(\frac{1}{6}\) x + 2 на отрезке [—6; 0]; г) у = — 1,2х на полуинтервале (—5; 5]; д) у = х — 4 на отрезке [—4; 4]; е) у = —0,5х + 3 на луче (—?; 6].
\( y = 2 — x \);
а) \( y_{\text{наим}} = -2 \); \( y_{\text{наиб}} = 5 \).
б) \( 0 \leq y \leq 2 \) при \( 0 \leq x \leq 2 \).
Дана функция:
\( y = 2 — x \)
Это линейная функция с угловым коэффициентом \( k = -1 < 0 \), следовательно, она **убывает** на всей области определения.
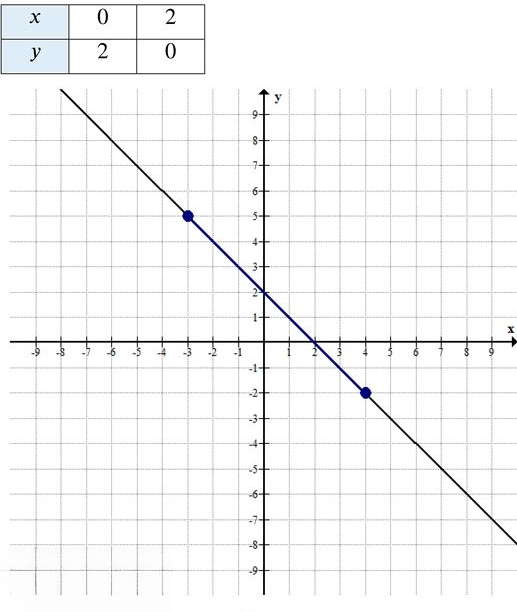
График — прямая, проходящая через точки, в которых можно найти значения \( y \) при заданных \( x \).
Таблица значений:
Найдём координаты двух точек для построения графика:
— При \( x = 0 \):
\( y = 2 — 0 = 2 \) → точка \( (0; 2) \)
— При \( x = 2 \):
\( y = 2 — 2 = 0 \) → точка \( (2; 0) \)
Таблица:
Через эти точки проходит график функции — прямая, направленная вниз направо.
а) Наименьшее и наибольшее значения функции
В пункте указано:
\( y_{\text{наим}} = -2 \), \( y_{\text{наиб}} = 5 \)
Эти значения достигаются при определённых границах области определения. Найдём, на каком промежутке это происходит.
Так как функция убывает, наибольшее значение достигается при наименьшем \( x \), а наименьшее — при наибольшем \( x \).
— Если \( y_{\text{наиб}} = 5 \), то:
\( 5 = 2 — x \) → \( x = 2 — 5 = -3 \)
— Если \( y_{\text{наим}} = -2 \), то:
\( -2 = 2 — x \) → \( x = 2 + 2 = 4 \)
Следовательно, эти экстремальные значения достигаются на промежутке \( x \in [-3; 4] \).
На этом отрезке:
— при \( x = -3 \): \( y = 5 \) — наибольшее значение,
— при \( x = 4 \): \( y = -2 \) — наименьшее значение.
б) Значения функции на отрезке \( [0; 2] \)
Рассмотрим функцию на промежутке \( x \in [0; 2] \).
Поскольку функция убывает:
— при \( x = 0 \): \( y = 2 \) — наибольшее значение,
— при \( x = 2 \): \( y = 0 \) — наименьшее значение.
Следовательно, при \( 0 \leq x \leq 2 \) значения функции изменяются от 2 до 0, то есть:
\[
0 \leq y \leq 2
\]
Это означает, что график на данном участке представляет собой отрезок прямой между точками \( (0; 2) \) и \( (2; 0) \), лежащий в первой координатной четверти.